本文首发于“嵌入式软件实战派”。
循环冗余校验(英语:Cyclic redundancy check,通称“CRC”)是一种根据网络数据包或电脑文件等数据产生简短固定位数校验码的一种散列函数,主要用来检测或校验数据传输或者保存后可能出现的错误。
Wikipedia
一句话:CRC是将数据计算出散列的方式,一般用于校验数据的完整性。它具有简单、执行效率高等特点。当然,你可以类比于Checksum,但比Checksum复杂些,防碰撞性更好些。
▍CRC的原理
CRC是基于除法的。实际的输入数据会被解释为一个长二进制位流(除数),再将其除以另一个固定二进制数(除数,即多项式)。该除法的其余部分就是校验值。
但是,现实要复杂一些。二进制数(除数和除数)不被视为普通整数值,而是被视为二进制多项式,其中实际位用作系数。
输入数据,看做一串二进制流,用多项式的方式表示为g(x),而除数是国际标准上的多项式,用h(x)表示。通过g(x)和h(x)做除法,即两者的异或运算,得出的结果,就是我们所说的CRC运算检验结果。
那么,这里有两个疑问:
问题1:多项式和二进制是什么关系?
例如,1x3 + 0x2 + 1x + 1可以表示为1011b,或者1011b表示为1x3 + 0x2 + 1x + 1,其中是0的位,即以0为系数乘以该项。
问题2:除法怎么做?
本质就是在做异或运算
我们来看看一个数据串100除以x3 + x + 1是怎样进行的?
注意,根据CRC长度,需要将这个数据串补0
![]()
整个运算过程是这样的:
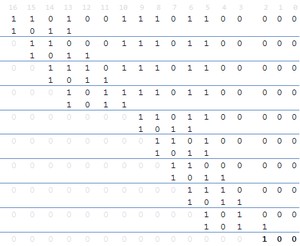
实际上就是逐个bit移位做异或。
详见:https://en.wikipedia.org/wiki/Cyclic_redundancy_check
▍CRC的概念
实际上,人们根据不同的需要,做了很多种计算方式,主要差别在于CRC长度、多项式、初始值、结果是否需要异或、是否需要翻转等等。
首先,来看看几个概念:
- Length: CRC的长度(按bit算,如8,16,32)
- Name: CRC的名字,让人一看就知道这是哪种CRC
- Polinomial: 多项式,通过该多项式来计算CRC
- InitialValue: CRC的初始值
- FinalXorValue: CRC结果做异或运算的值
- InputReflected: 指示输出是否需要翻转
- OutputReflected: 指示输出是否需要翻转
我将网上搜到的所有的CRC标准分类做了个汇总:
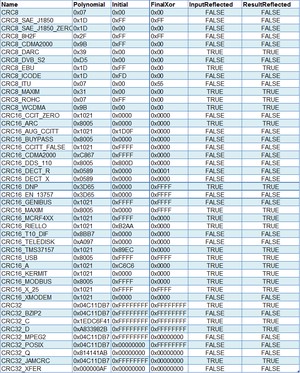
从上面的CRC名称可以看出,不同的算法是有不同用途的,这是国际常规的用法定义,其实如果是用户自己用也没特别要求,可以自由点。
▍CRC的实现
1. 根据多项式二进制数,逐位做异或
按照前面章节的“CRC原理”来做C语言实现,就通过数据移位和异或算得。以CRC8为例,代码如下
这个代码中有个if ((crc & 0x80u) > 0)要解释下,因为任意数与0做异或,结果是其本身。所以,数据为0时,不做异或。同理,CRC16、CRC32也可以按这种方法做计算,只是多项式和数据位数不一样而已,在此不累述了。
按移位做异或的方法,有个缺点,就是用了两层循环,效率不是那么的高,在嵌入式软件中,不是那么受欢迎。
那需要怎么优化算法呢?那就将多项式预先算个表出来,查表吧。
2. 将多项式(Polynomial)生成一个256长度的表,用查表法实现
2.1 多项式生成的表
在开始这个话题之前,我们得回个头来看看那几个概念中有个InputReflected和OutputReflected。干啥呢,吃饱没事干啊,算就算,还要翻转?呵呵!
其实,通过多项式生成表就可以生成正序和逆序,就是为了应付这个“翻转”的。举个例子以CRC8_ITU(Polynomial=0x07)看看这个表:
正序表为
2.2 通用查表法
网上有很多种查表发计算CRC,不尽相同。于是我做了个通用版,满足各种算法,其中用了宏定义的奇技淫巧。直接上代码:
怎么用?
先定义,即定义对于位数算法的函数,通过预编译生成:
再调用,测试可以在main函数调用:
这里还是有个问题,就那个“翻转”的问题,每个byte都做翻转,很浪费CPU资源啊。作为“优秀的”嵌入式软件开发人员,我们是追求卓越的算法,于是乎,就有了以下方式:
(1)对于InputReflected和OutputReflected都是False的,我们用正序表,以CRC8_ITU为例:
(2)对于InputReflected和OutputReflected都是True的,我们用逆序表,以CRC8_EBU为例:
▍CRC的源码
说了这么多,以上都是举例而已(其实直接将上面代码copy过去验证也是木有问题的,不要怀疑),上代码啊
Talk is cheap. Show me the code.
Linus Torvalds
我将上面表格中提到的所有CRC算法,都coding了,就像下图的这些
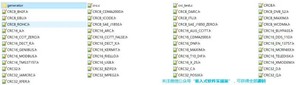
举个例子,CRC32_BZIP2.h文件是的算法是这样的:
![]()
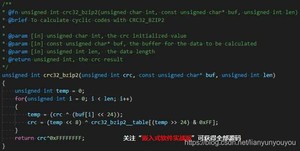
真以为我一个一个写的吗,哈哈哈,不是。但我肯定不是在网上一个一个抄的,网上也找不到这么多。
还是那句话:机器能干的事,为啥还要人来干!
我找到了个规律,写了个脚本生成的,多项式的正序表、逆序表是生成的,连代码,我都是用脚本生成的。
这里篇幅有限,就不将代码全部贴在这了,如果你对这些算法感兴趣,关注“嵌入式软件实战派”,聊天界面输入并发送“CRC”获得下载链接,或者点击[链接]下载。后续适当的时候,我还会将这个生成源文件的脚本也分享给大家。
为了验证其可靠性,我还做了个测试代码(篇幅有限,下面截取的代码已省略了部分):
如果你怀疑我“监守自盗”,你还可以在网上找个在线计算的方式来验证算法的正确性,如:https://crccalc.com/
如果有其他想法和建议,请留言,我们一同探讨。
如果你喜欢我的文章,请扫码关注“嵌入式软件实战派”,我会分享更多技术干货。

版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/14366.html
