TODO:
在阅读本文之前,您可能需要先了解位运算、二叉树以及前缀和与差分等相关知识
本文中,若无特殊说明,数列下标均从 开始
树状数组是一种 通过数组来模拟"树形"结构,支持单点修改和区间查询的数据结构
因为它是通过二进制的性质构成的,所以它又被叫做 二进制索引树(),也被称作
树状数组常用于动态维护区间信息
P3374 【模板】树状数组 1 - 洛谷
题目简述:对数列进行单点修改以及区间求和
单点修改的时间复杂度为
区间求和的时间复杂度为
共 次操作,则总时间复杂度为
区间求和通过前缀和优化,但单点修改的时候需要修改前缀和数组
单点修改的时间复杂度为
区间求和的时间复杂度为
共 次操作,则总时间复杂度为
可以发现上述两种方法,不是单点修改的时间复杂度过高,就是区间求和的时间复杂度过高,导致最坏时间复杂度很高。
于是,树状数组出现了,它用来平衡这两种操作的时间复杂度。
树状数组的思想
每个正整数都可以表示为若干个 的幂次之和(二进制基本原理)
类似的,每次求前缀和,我们也希望将区间 分解成 个子集的和
也就是如果 的二进制表示中如果有 个 ,我们就希望将其分解为 个子集之和
树状数组的树形态与二叉树
每一个矩形代表树的一个节点,矩形大小表示所管辖的数列区间范围
一颗二叉树的形态如下图所示
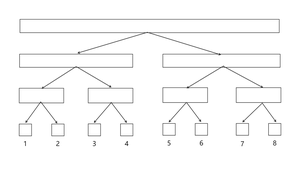
我们发现,对于具有逆运算的运算,如求和运算,有如下式子
实际上,许多数据可以通过一些节点的差集获得
因此,上述二叉树的一些节点可以进行删除
树状数组的形态如下图所示
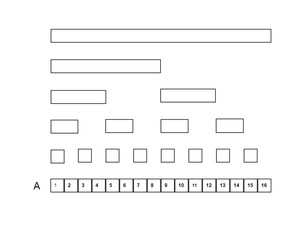
管辖区间
对于下图中的树状数组(黑色数字代表原始数组 红色数字代表树状数组中的每个节点数据 )
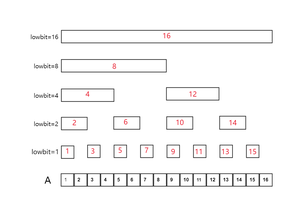
从图中可以看出:
那么如何通过计算机确定 的管辖区间呢?
前面提到过树状数组的思想是基于二进制的
树状数组中,规定 所管辖的区间长度为 ,其中:
- 设二进制最低位为第 位,则 恰好为 的二进制表示中,最低位的 所在的二进制位数;
- ( 的管辖区间长度)恰好为 二进制表示中,最低位的 以及后面所有 组成的数。
以 所管辖的区间为例
因为 ,其二进制最低位的 及后面的 组成的二进制是 ,所以, 管理 个 数组中的元素。
因此, 代表 的区间信息。
我们记 二进制最低位 以及后面的 组成的数为 ,则 管辖的区间就是
其中
树状数组树的性质
性质比较多,下面列出重要的几个性质,更多性质请参见OI Wiki,下面表述忽略二进制前导零
- 节点 的父节点为
- 设节点 ,则其儿子数量为 (即 的二进制表示中尾随 的个数),这 个儿子的编号分别为
如 , 的二进制表示为 ,则 有三个儿子,这三个儿子的二进制编号分别为 、、
- 节点 的所有儿子对应 的管辖区间恰好拼接成
- 如 , 的二进制表示为 , 的三个儿子的二进制编号分别为 、、
表示,表示,表示
上述三个儿子管辖区间的并集恰好是 ,即
- 如 , 的二进制表示为 , 的三个儿子的二进制编号分别为 、、
单点修改
根据管辖区间,逐层维护管辖区间包含这个节点的父节点(节点 的父节点为 )
区间查询
区间查询问题可以转化为前缀查询问题(前缀和思想),也就是查询区间 的和,可以转化为 与的差集
如计算 的值,可以转化为求 和 再相减
前缀查询的过程是:根据管辖区间,不断拆分区间,查找上一个前缀区间
对于 的前缀查询过程如下:
- 从 开始向前拆分,有 管辖
- 令
- 重复上述过程,直至
由于 的算术意义是去除二进制最后一个 ,因此也可以写为
上述过程进行了两次前缀查询,实际上,对于 和 的前缀区间是相同的,我们不需要计算
单点查询
单点查询可以转化为区间查询,需要两次前缀查询,但有更好的方法
所管辖的区间为 ,而节点 的所有子节点的并集恰好为
则
对于 的更好的查询过程如下:
- 查询 所管辖的区间
- 减去 的所有子节点的数据
建树
可以通过调用单点修改方法进行建树,时间复杂度
时间复杂度为 的建树方法有如下两种:
方法一:
每一个节点的值是由所有与自己直接相连的儿子的值求和得到的。因此可以倒着考虑贡献,即每次确定完儿子的值后,用自己的值更新自己的直接父亲。
方法二:
由于 所管辖的区间是 ,则可以预处理 前缀和数组,再通过 计算
我们也可以先用 数组计算前缀和,再倒着计算 (因为正着计算会导致前面的值被修改,与 背包优化相同)
同样的 可以写为
复杂度分析
空间复杂度为
单点修改、单点查询、区间查询操作的时间复杂度均为
建树的时间复杂度为 或
Code
- 注意树状数组的树型特征
- 的管辖元素个数为,管辖区间为
- 树状数组中, 的父节点编号为
- 树状数组的二叉查找树中, 的父节点(也即前缀区间)编号为
- 树状数组是一个维护前缀信息的树型数据结构
- 树状数组维护的信息需要满足结合律以及可差分(因为一些数据需要通过其他数据的差集获得)两个性质,如加法,乘法,异或等
结合律:,其中 是一个二元运算符。
可差分:具有逆运算的运算,即已知 和 可以求出
- 有时树状数组在其他辅助数组(如差分数组)的帮助下,可以解决更多的问题
- 由于树状数组需要逆运算抵消掉原运算(如加和减),而线段树只需要逐层拆分区间,在合并区间信息,并不需要抵消部分数值,所以说树状数组能解决的问题是线段树能解决的问题的子集
- 树状数组下标也可以从 开始,此时 的父节点编号为 , 的管辖元素个数为 ,管辖区间为
- 树状数组常常通过离散化这一技巧缩小数据范围来减少空间
- 树状数组是一种工具,许多问题可以借助这个工具解决,就如同滑动窗口可以借助双端队列解决一样
一个 的树状数组封装类
P3368 【模板】树状数组 2 - 洛谷
一些操作映射到前缀数组或者差分数组上可能会变得很简单
考虑序列 的差分数组 ,其中 。
则对于序列 的区间 加 可以转化为 和 ,也就是差分数组上的两次单点操作。
因此 选择通过树状数组维护差分数组
P3372 【模板】线段树 1 - 洛谷
对于区间查询 ,同样选择转化为前缀查询 及 的差集
考虑序列 的差分数组 ,其中 。由于差分数组的前缀和就是原数组,则
所以,前缀查询变为
上式可表述为下图蓝色部分面积
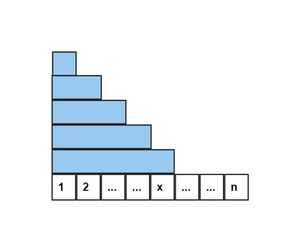
横着看看不出什么,但竖着看会发现每个数据加的个数与 有关
会加 次, 会加 次, , 会加 次, 会加 次
也就是 会加 ,加法转化为乘法可得
又因为 与 不能推导推导出另一个
因此需要用两个树状数组分别维护 与
- 用于维护 的树状数组,对于每次对 加 转化为 与
- 用于维护 的树状数组,对于每次对 加 转化为
与
即在原来的基础上加上 与减去
也可以写成封装类的形式
题目链接
题意简述:有两个操作
- 对区间 的数均加
- 查询第 个数的值
进阶中的 区间修改+单点查询
题目链接
题目简述:有两个操作
- 对区间 的数进行反转(1变0,0变1)
- 单点查询
反转等同于与 异或,于是题目变成了维护区间异或和单点查询,同样选择差分序列,只不过是异或的差分。
而异或也满足树状数组的两个要求,因此使用树状数组解决该题
题目链接
题意简述:求数组中的逆序对
求解逆序对可以用归并排序求解,此处不做讨论
从前向后遍历数组,同时将其加入到桶中,记录每个数出现的个数,并加上该位置之前且比当前数大的数的个数(有点绕,看例子可能会清晰点)
桶:用 表示目前 出现的个数,初始化均为
:表示目前逆序对的个数,初始化为
也就是需要求 时刻,桶中 的和,其中 为所有数据中的最大值
也即实现 单点加 与 区间查询,使用树状数组求解
但是题目中 ,树状数组的长度开不了那么大
可以发现,该题中我们只关心数据间的相对大小关系,而不关心数据本身大小,采用离散化的方式,将数据缩小(一种映射关系)
举个例子:
代码如下:
题目链接
同样是求逆序对,但是需要求的是每个位置的逆序对数量,就不能像上面那样顺序遍历了
题目链接
题意简述:有两个操作
- 单点赋值
- 区间和查询
单点赋值可以改为单点查询+单点修改(查询这个值再减去这个值)
当然也可以多开一个 数组维护单点值
树状数组 - OI Wiki
超详细的树状数组详解 - 蒟蒻kingxbz的小窝
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/8655.html
