二叉排序树构造过程



（1）若左子树不空，则左子树上所有结点的值均小于或等于它的根结点的值；
（2）若右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值；
（3）左、右子树也分别为二叉排序树；

public LinkedList inorder(TreeNode root, LinkedList arr) {
if (root == null) return arr;
inorder(root.left, arr);
arr.add(root.val);
inorder(root.right, arr);
return arr;
}

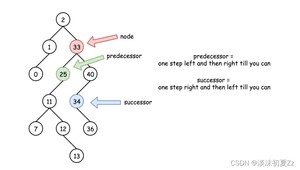
public int successor(TreeNode root) {
root = root.right;
while (root.left != null) root = root.left;
return root;
}

public int predecessor(TreeNode root) {
root = root.left;
while (root.right != null) root = root.right;
return root;
}

（1）若value < root.val，则在左子树进行删除
（2）若value >root.val，则在右子树进行删除
（3）若value == root.val，此节点就是要删除的

① 该节点是叶子，直接删除
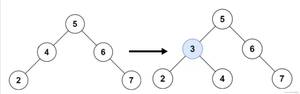
②该节点只有左子树，将前驱节点代替根节点，删除前驱节点
③该节点只有右子树，将后继节点代替根节点，删除后继节点

（4）返回根节点root

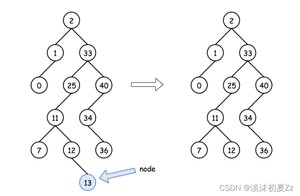
（1）要删除的节点为叶子节点，可以直接删除

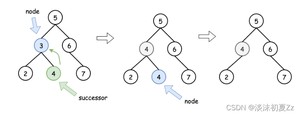
（2）删除的节点不是叶子节点，只有右节点，则该节点可以由该节点的后继节点替代，然后可以从后继节点的位置递归向下操作以删除后继节点。

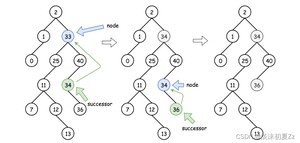
（3）删除的节点不是叶子节点，只有左节点。这意味着它的后继节点在它的上面，但是我们并不想返回。我们可以使用它的前驱节点进行替代，然后再递归的向下删除前驱节点。

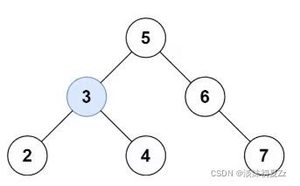
🍎 (1)查找二分搜索树是否包含指定值-二分查找
🍎 (2)返回二分搜索树的最小值
🍎 (3)返回二分搜索树的最大值

（1）⭐优势⭐
查找元素、插入元素、删除元素的时间复杂度都是O(logn)。还可以方便的回答很多数据之间关系的问题:min，max，floor，ceil，rank，select
（2）⭐局限性⭐
当将一组数据以近乎有序的顺序插入空二分搜索树中时，几乎每一个节点都是父节点的右孩子，二分搜索树近乎退化成了一个链表，相关算法时间复杂度都退化成了O(N)。因此有了平衡二叉树，不会退化成链表，如：红黑树等。

版权声明：

本文来源网络，所有图片文章版权属于原作者，如有侵权，联系删除。

本文网址：https://www.mushiming.com/mjsbk/6558.html