目录
基本思想
代码
合并两组有序序列
归并排序
1.递归
2.循环
复杂度与稳定性
时间复杂度
空间复杂度
完整代码
从以上图中可以看出,归并排序就是不断的将两组有序的序列进行合并(第一次将单独的一个元素当作一组有序序列),从而得到最终的排序结果。所以首先给出如下一段代码,用来合并两组有序的序列(排升序):
以上代码中,因为合并时数字都在同一数组当中,所以它们的下标是连续的,在合并时需要使用新的空间来放合并后的结果,注意:合并后的结果应该放在新申请出的空间的对应位置,即count必须从left开始,因为在以下代码中需要拷贝。
1.递归
有了上述合并两组有序序列的代码,那么很容易就会想到使用递归来对一组序列进行归并,直接看代码:
上述递归过程中不断将问题的规模缩小,直到对两个元素进行排序,而后在层层处理其余部分。归并排序的递归格式有点像二叉树的后序遍历,很方便记忆。注意:每次归并完一组数据,都要把归并好的结果拷贝回原来的空间,还要注意当前拷贝的位置与拷贝的元素个数。
2.循环
递归可能不是很好理解,但是循环就比较简单了。可以先两个一组进行归并,全部归并完成后,在四个四个一组进行归并..........代码如下:
当gap=1时,此时每两个元素一组,把这两个元素进行了排序,然后不断将数组元素划分为两个一组,全部排序。到下一次gap就会增长2倍,此时四个元素一组,重复上述过程。直到gap>size,说明整个归并排序结束。注意:此时的拷贝只需要在gap变化之后进行整体拷贝。
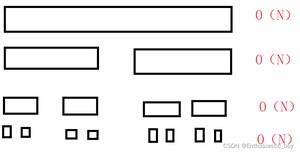
排序的过程像是一颗二叉树,每一层表示归并这层元素,复杂度为O(N),深度为logN,所以整体的时间复杂度为:O(NlogN)
每次在堆上申请的空间大小与原数组相同,所以空间复杂度为:O(N)
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/3312.html
