树状数组简单易懂的详解



根据维基百科的定义：

A Fenwick tree or binary indexed tree is a data structure that can efficiently update elements and calculate prefix sums in a table of numbers.

也就是说，所谓树状数组，或称Binary Indexed Tree, Fenwick Tree，是一种用于高效处理对一个存储数字的列表进行更新及求前缀和的数据结构。

举例来说，树状数组所能解决的典型问题就是存在一个长度为的数组，我们如何高效进行如下操作：

1. ：将加到位置的数字上。
2. ：求从数组第一个位置到第（含）个位置所有数字的和。
3. ：求从数组第个位置到第个位置的所有数字的和

对于上述问题，除去每次求和都对原数组相关数字暴力相加求和的解法外，另一种较简单解法为使用时间构造一个_前缀和数组（cumulative sum）_，即该数组中的第个位置保存原数组中前个元素的和，则对于上述每一个操作，我们有：

1. ：更新操作需要更新cumulative sum数组中每一个受此更新影响的前缀和，即从其到最后一个位置的前缀和。该操作为时间复杂度。
2. ：直接返回即可。该操作为时间复杂度。
3. ：直接返回即可。该操作为操作。

可以看出，该简单解法的求和操作非常高效，而单个更新操作为线性时间。如果所需的更新操作的数量远少于求和操作的话，该解法非常合适。反之，如果更新操作较多，我们就需要思考优化的方法。

那么使用树状数组解决该问题的目的就是为了在保证求和操作依然高效的前提下优化 操作的时间复杂度。

所谓的Binary Indexed Tree，首先需要明确它其实并不是一棵树。Binary Indexed Tree事实上是将根据数字的二进制表示来对数组中的元素进行逻辑上的分层存储。

Binary Indexed Tree求和的基本思想在于，给定需要求和的位置，例如13，我们可以利用其二进制表示法来进行分段（或者说分层）求和：，则 （注意此处的表示数组中第个位置到第个位置的所有数字求和）。如下面例子中所示：

那么如果我们将上述的range sum提前计算好的话，可以直接由它们相加得到。那么我们所需要解决的问题就是，根据何种规则来计算和存储这样的二进制表示后所需的range sum呢？规则如下图中所示。

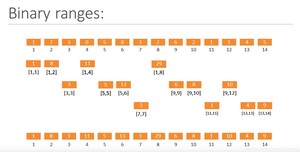
图中第一行为原数组，第二到第四行为依次按层填坑的过程。我们需要从左到右，从上到下依次将相应的值填入对应的位置中。最后一行中即为最终所形成的树状数组。

以图中第二行，也就是构造树状数组第一层的过程为例，我们首先需要填充的是数组中第一个数字开始，长度为__2的指数__个数字的区间内的数字的累加和。所以图中分别填充了从第一个数字开始，长度为的区间的区间和。到此为止这一步就结束了。因为超过了我们原数组的长度范围。

下一步我们构造数组的第二层。与上一层类似，我们依然填充余下的空白中从第空白处一个位置算起长度为__2的指数__的区间的区间和。例如空白，我们只需填充从位置3开始，长度为1的区间的和。再如空白，我们需要填

版权声明：

本文来源网络，所有图片文章版权属于原作者，如有侵权，联系删除。

本文网址：https://www.mushiming.com/mjsbk/1430.html