已同步微信公众号【乐享Coding】,想要一起学习的可以加群,共同交流!
基本思想:
将所有待比较数值统一为同样的数位长度,数位较短的数前面补零。
从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。
理论比较晦涩难懂,我们以具体例子进行图解:
本次举例的待排序数组为:[1, 52, 478, 12, 83, 7, 45, 333 ]
大家先可以看看排序的步骤,进一步对思路有个大致理解!
步骤一
准备是10个桶(0-9),取数组中每一个元素个位的值,分别装入对应的桶中。
根据动图可以看到桶应该是个,既要有编号(0-9),又要存数据(0-arr.length)。
代码实现:
定义桶(二维数组):
除了桶这个需要额外空间之外,我们还需要一个数组来记录每个桶中的元素个数,目的是方便最后取出。
在此,我们还可以发现一个问题就是可能会存在空桶占用空间资源,所以基数排序典型的占用空间换取时间,文章末尾会对这种排序时间和空间复杂度的分析!
在个位排序之后bucketElementCounts数组的应该为:
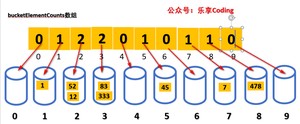
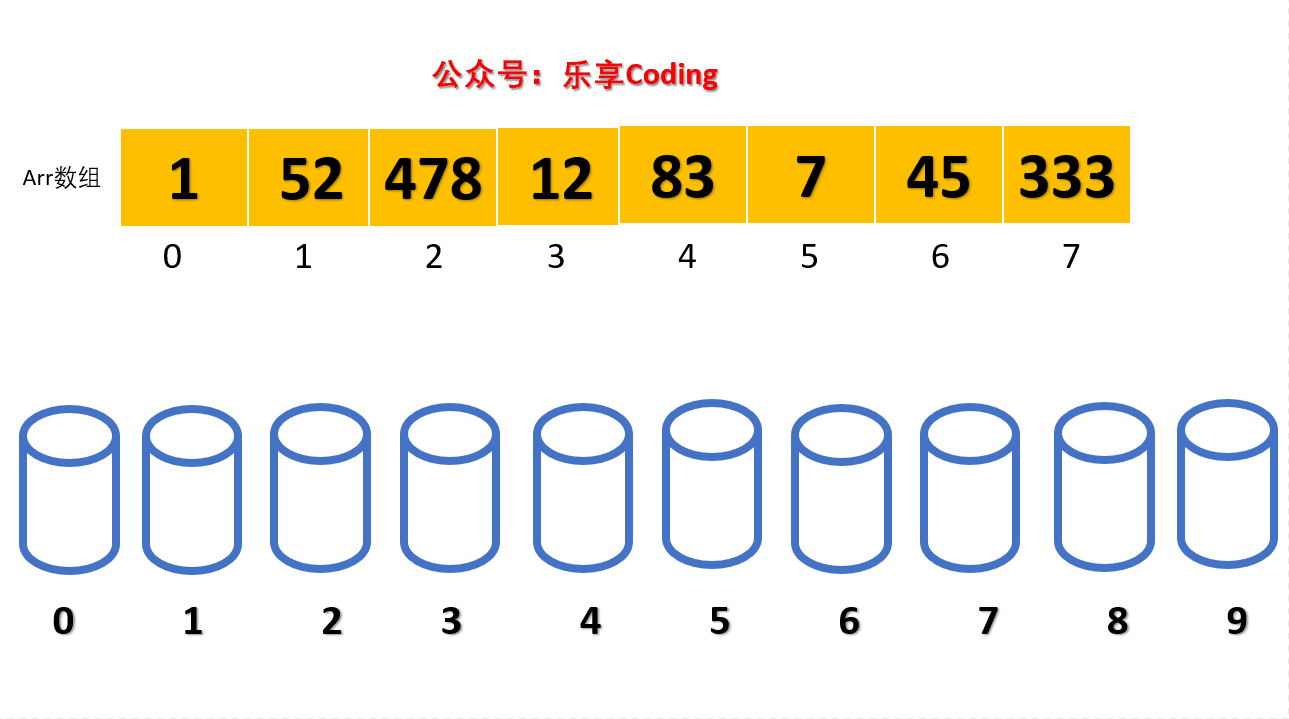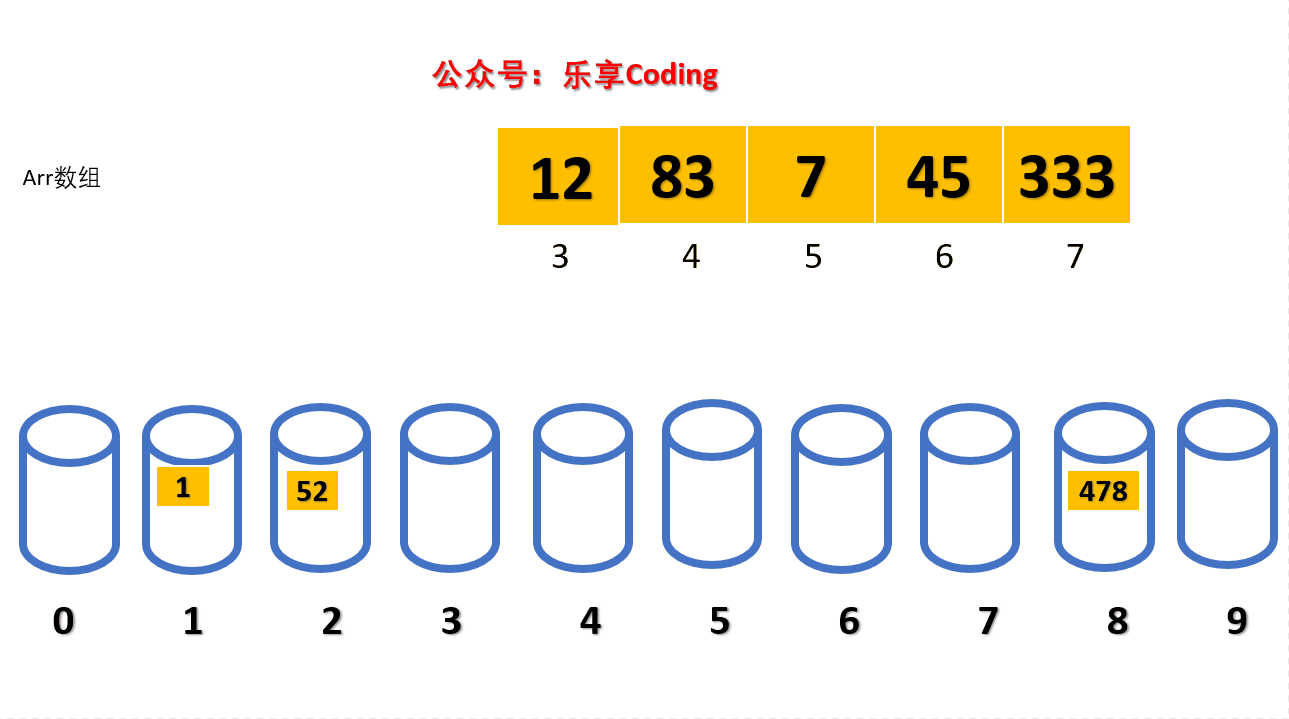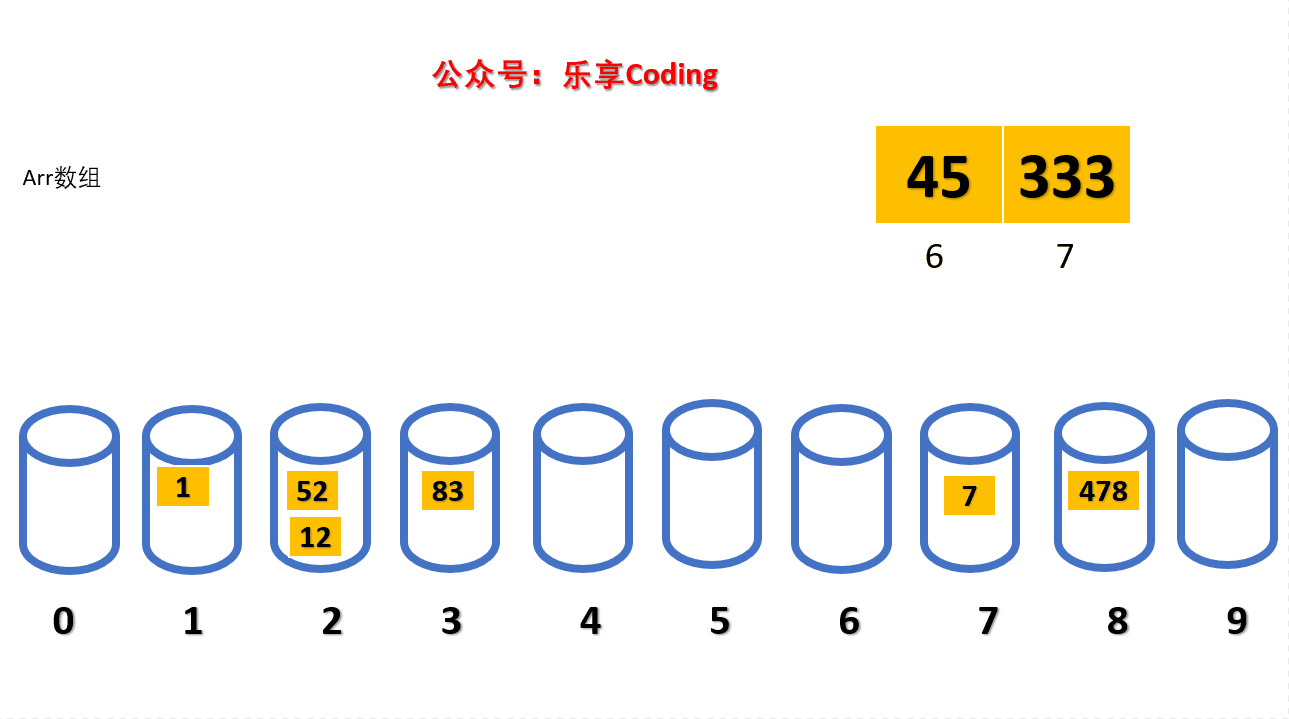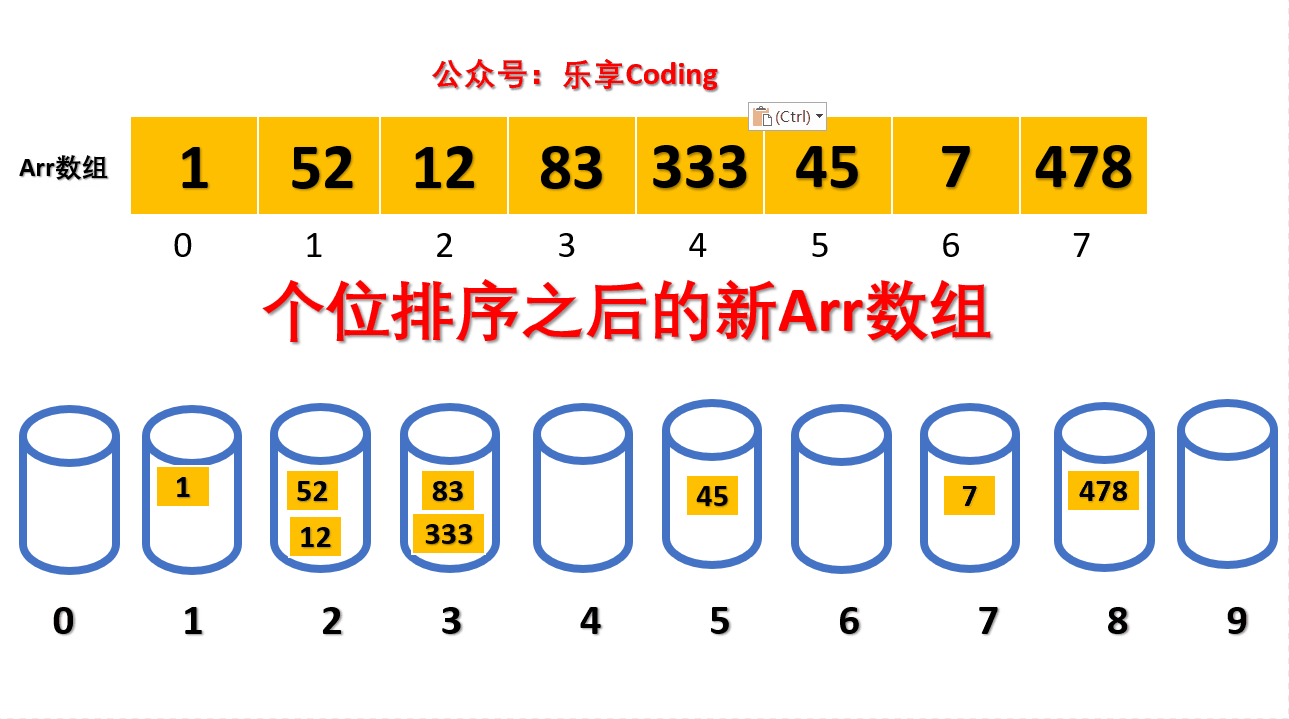
之后根据以下代码将桶中元素取出替换arr数组
上述排序后的新arr数组为

步骤二:第一次是找个位接下来就是找十位的数字,重复步骤一,在找出百位的数字,同样重复步骤一。最后arr数组就会按照升序排序结束。
在此只展示代码不同的地方,其余地方完全一样。
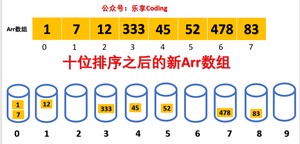
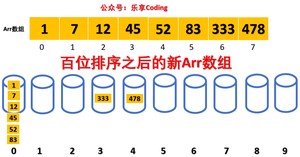
此时arr数组已经成了完全升序的数组了。
优化
最后我们总结以下可以优化的,此次排序一共进行了三轮,且每轮都有重复代码,因此这样是非常冗余的。
观察发现与最大元素的位数有关,联想简单选择排序我们可知只需找出最大值,最大值占几位,那么就需要循环几轮。
本例最大元素是478,共占三位,所以需要循环三轮,通过改进代码我们得到了最终代码:
时间和空间复杂度分析
空间复杂度:
- 最坏情况下:O(m*n) m代表“桶”的个数,一般是10。
时间复杂度:O(m+n)
- m是保存桶的元素个数数组占的空间,n是保存桶的二维数组占的空间。
最后总结
1)基数排序是对传统桶排序的扩展,速度很快.
2)基数排序是经典的空间换时间的方式,占用内存很大, 当对海量数据排序时,容易造成 OutOfMemoryError 。
3)基数排序时稳定的(值相等的元素排序后前后顺序不变)。
4)有负数的数组,我们不用基数排序来进行排序, 如果要支持负数,需要添加绝对值并反转。

版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/12275.html
