`# 二叉树的深度优先遍历(前序,中序,后序) 和 广度优先遍历(层次遍历)
引言
在计算机科学中,二叉树是一种常用的树结构,每个节点最多有两个子节点。二叉树遍历是访问树中每个节点的一种方法。二叉树的遍历分为深度优先遍历(DFS)和广度优先遍历(BFS)。本文将详细介绍这两种遍历方式及其应用。
深度优先遍历会尽可能沿着树的深度访问节点,直到树的叶子节点,然后回溯到最近的分支继续遍历。深度优先遍历主要分为三种方式:
前序遍历(Pre-order Traversal):访问根节点 -> 左子树 -> 右子树
中序遍历(In-order Traversal):访问左子树 -> 根节点 -> 右子树
后序遍历(Post-order Traversal):访问左子树 -> 右子树 -> 根节点
下面我们给出一个二叉树,分别看看三种遍历方式``
前序遍历(Pre-order Traversal)
访问根节点 -> 左子树 -> 右子树
下面先用图来介绍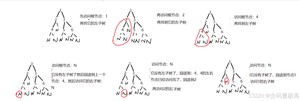

这就是一次先序遍void PreOrder(BTNode* root)//先序遍历

中序遍历(In-order Traversal)
访问左子树 -> 根节点 -> 右子树
还是先用图来介绍
这就是一次中序遍历的过程

后序遍历(Post-order Traversal)
访问左子树 -> 右子树 -> 根节点
还是先用图来介绍

这就是一次后序遍历的过程

广度优先遍历是逐层从上到下、从左到右遍历树的节点,常用于找最短路径等问题。
层序遍历的原理
层序遍历以树的根节点开始,按照从上到下、从左到右的顺序逐层遍历树中的节点。这意味着在遍历当前层的节点之前,需要先遍历完上一层的节点。层序遍历基于队列的数据结构实现,它的过程可以描述如下:
1.创建一个队列,并将根节点入队。
2.当队列不为空时,执行以下步骤:
从队列中取出一个节点,访问该节点。
将该节点的所有子节点(如果存在)依次入队。
3.如果队列为空,则表示遍历结束。
由于队列的特性,首先入队的节点会先被访问,保证了按照层级顺序遍历节点。

代码实现

这就是一次层次遍历的过程
深度优先遍历:适用于路径查找和递归操作,空间复杂度较小。
广度优先遍历:适用于最短路径问题,空间复杂度较大。
在实际应用中
前序遍历:复制树、表达式树计算。
中序遍历:二叉搜索树排序。
后序遍历:删除节点、计算树的高度。
层次遍历:最短路径、树的层次表示。
掌握二叉树的深度优先遍历和广度优先遍历,对于算法设计和树结构问题的解决至关重要。根据实际需求选择合适的遍历方法,可以大大提高算法的效率。
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/1193.html
