强化学习是机器学习中的一大分支,通过与环境的交互,通过不断试错来学习如何做出最优决策。Deep Q-Network(DQN)算法是强化学习中的经典算法之一,它结合了深度学习和Q-learning算法,可以在宽泛的任务领域中学习和解决问题。

一、简介
DQN算法是深度学习领域首次广泛应用于强化学习的算法模型之一。它于2013年由DeepMind公司的研究团队提出,通过将深度神经网络与经典的强化学习算法Q-learning结合,实现了对高维、连续状态空间的处理,具备了学习与规划的能力。
二、发展史
在DQN算法提出之前,强化学习中的经典算法主要是基于表格的Q学习算法。这些算法在处理简单的低维问题时表现出色,但随着状态和动作空间的增加,表格表示的存储和计算复杂度呈指数级增长。为了解决这个问题,研究人员开始探索使用函数逼近的方法,即使用参数化的函数代替表格。
Q-learning:Q-learning是强化学习中的经典算法,由Watkins等人在1989年提出。它使用一个Q表格来存储状态和动作的价值,通过不断更新和探索来学习最优策略。然而,Q-learning算法在面对大规模状态空间时,无法扩展。
Deep Q-Network(DQN):DQN算法在2013年由DeepMind团队提出,通过使用深度神经网络来逼近Q函数的值,解决了状态空间规模大的问题。该算法采用了两个关键技术:经验回放和固定Q目标网络。
经验回放:经验回放是DQN算法的核心思想之一,它的基本原理是将智能体的经验存储在一个回放记忆库中,然后随机从中抽样,利用这些经验进行模型更新。这样做的好处是避免了样本间的相关性,提高了模型的稳定性和收敛速度。
固定Q目标网络:DQN算法使用两个神经网络,一个是主网络(online network),用于选择动作,并进行模型更新;另一个是目标网络(target network),用于计算目标Q值。目标网络的参数固定一段时间,这样可以减少目标的波动,提高模型的稳定性。
三、算法公式
DQN算法的核心是Q-learning算法和深度神经网络的结合。

其中,s_t表示当前状态,a_t表示选择的动作,r_t表示立即回报,s_t+1表示下一个状态,α是学习率,γ是折扣因子。
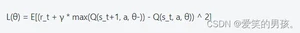
其中,θ是网络参数,Q(s_t, a, θ-)表示目标网络的输出。
四、算法原理
DQN算法的原理是通过利用深度神经网络逼近Q函数的值,实现对高维、连续状态空间的处理。其核心思想是通过不断更新神经网络的参数,使其的输出Q值逼近真实的Q值,从而学习最优策略。
DQN算法的工作原理如下:
初始化:初始化主网络和目标网络的参数。
选择动作:根据当前状态s,使用ε-greedy策略选择动作a。
执行动作并观察回报:采取动作a,与环境交互,观察下一个状态s’和立即回报r。
存储经验:将(s, a, r, s’)存储到经验回放记忆库中。
从经验回放记忆库中随机抽样:从记忆库中随机抽样一批经验。
计算目标Q值:使用目标网络计算目标Q值,即max(Q(s’, a, θ-))。
更新主网络:根据损失函数L(θ)进行模型参数更新。
更新目标网络:定期更新目标网络的参数。
重复步骤2-8,直到达到终止条件。
五、算法功能
DQN算法具有以下功能:
处理高维、连续状态空间:通过深度神经网络的逼近能力,可以处理高维、连续状态空间的问题。
学习和规划能力:通过与环境的交互和不断试错,DQN算法可以学习到最优策略,并具备一定的规划能力。
稳定性和收敛速度高:DQN算法通过经验回放和固定Q目标网络等技术,提高了模型的稳定性和收敛速度。
六、示例代码
以下是一个使用DQN算法解决经典的CartPole问题的示例代码:
运行结果:

通过运行以上代码,可以看到DQN算法在解决CartPole问题上的表现。在经过多个episode的训练后,算法可以在游戏中坚持更久的时间,最终取得较高的得分。
七、总结
本文对DQN算法进行了详细的讲解,包括发展史、算法公式和原理、功能、示例代码以及如何使用。DQN算法通过结合深度学习和Q-learning算法,实现了对高维、连续状态空间的处理,具备了学习和规划的能力。通过示例代码的运行结果,我们可以看到DQN算法在解决CartPole问题上取得了较好的效果。然而,DQN算法也存在一些局限性,比如训练不稳定、样本相关性等问题。未来的研究可以进一步改进算法,并将其应用于更广泛的任务领域。
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/10990.html
