这是小川的第385次更新,第413篇原创
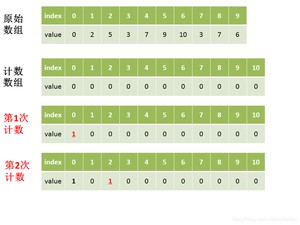
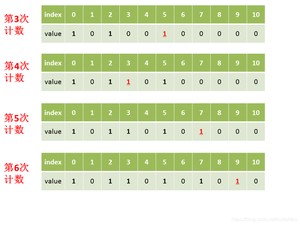
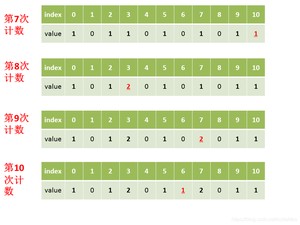
第一步:找出原数组中元素值最大的,记为。
第二步:创建一个新数组,其长度是加1,其元素默认值都为0。
第三步:遍历原数组中的元素,以原数组中的元素作为数组的索引,以原数组中的元素出现次数作为数组的元素值。
第四步:创建结果数组,起始索引。
第五步:遍历数组,找出其中元素值大于0的元素,将其对应的索引作为元素值填充到数组中去,每处理一次,中的该元素值减1,直到该元素值不大于0,依次处理中剩下的元素。
第六步:返回结果数组。
基础版能够解决一般的情况,但是它有一个缺陷,那就是存在空间浪费的问题。
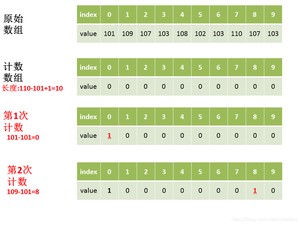
比如一组数据,其中最大值为110,按照基础版的思路,我们需要创建一个长度为111的计数数组,但是我们可以发现,它前面的的空间完全浪费了,那怎样优化呢?
将数组长度定为,即不仅要找出最大值,还要找出最小值,根据两者的差来确定计数数组的长度。
以数组为例。
第一步:找出数组中的最大值、最小值。
第二步:创建一个新数组,其长度是max-min加1,其元素默认值都为0。
第三步:遍历原数组中的元素,以原数组中的元素作为数组的索引,以原数组中的元素出现次数作为数组的元素值。
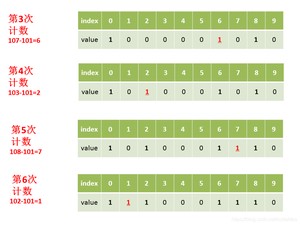
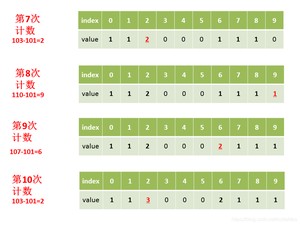
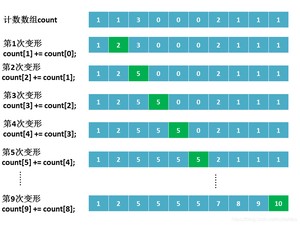
第四步:对数组变形,新元素的值是前面元素累加之和的值,即。
第五步:创建结果数组,长度和原始数组一样。
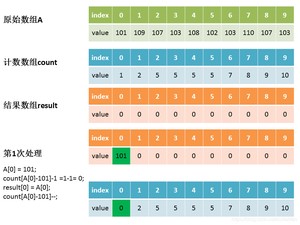
第六步:遍历原始数组中的元素,当前元素A[j]减去最小值,作为索引,在计数数组中找到对应的元素值,再将count[A[j]-min]的值减去1,就是在结果数组中的位置,做完上述这些操作,自减1。
是不是对第四步和第六步有疑问?为什么要这样操作?
第四步操作,是让计数数组存储的元素值,等于原始数组中相应整数的最终排序位置,即计算原始数组中的每个数字在结果数组中处于的位置。
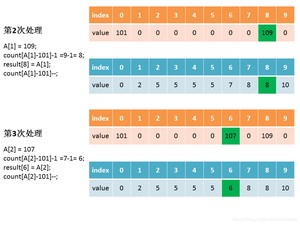
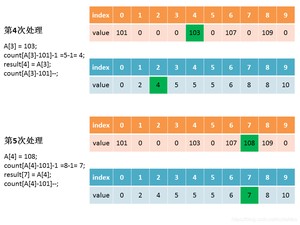
比如索引值为9的,它的元素值为10,而索引9对应的原始数组中的元素为9+101=110(要补上最小值,才能还原),即110在排序后的位置是第10位,即result[9] = 110,排完后的值需要减1,变为9。
再比如索引值为6的,他的元素值为7,而索引6对应的原始数组中的元素为6+101=107,即107在排序后的位置是第7位,即,排完后的值需要减1,变为6。
如果索引值继续为6,在经过上一次的排序后,的值变成了6,即107在排序后的位置是第6位,即,排完后的值需要减1,变为5。
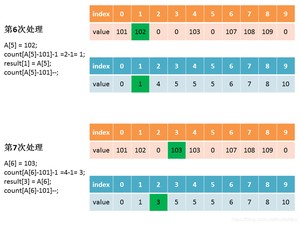
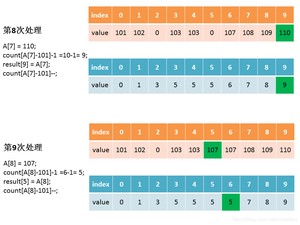

如果我们想要原始数组中的相同元素按照本来的顺序的排列,那该怎么处理呢?
依旧以上一个数组为例,其中有两个107,我们要实现第二个107在排序后依旧排在第一个107的后面,可以在第六步的时候,做下变动就可以实现,用倒序的方式遍历原始数组,即从后往前遍历数组。
从后往前遍历,第一次遇到107()时,107-101 = 6,,即第二个107要排在第7位,即,排序后。
继续往前,第二次遇到107()时,107-101 = 6,,即第一个107要排在第6位,即,排序后。
既然从后往前遍历原始数组的元素可以保证其原始排序,那么从前往后可不可以达到相同的效果?
答案时可以的。
第一步:找出数组中的最大值、最小值。
第二步:创建一个新数组,其长度是,其元素默认值都为0。
第三步:遍历原数组中的元素,以原数组中的元素作为数组的索引,以原数组中的元素出现次数作为数组的元素值。
第四步:对数组变形,新元素的值是前面元素累加之和的值,即。
第五步:创建结果数组,长度和原始数组一样。
第六步:从前往后遍历原始数组中的元素,当前元素减去最小值,作为索引,在计数数组中找到对应的元素值,就是在结果数组中的位置,做完上述这些操作,自增加1。
依旧以上一个数组为例,其中有两个107,我们要实现第一个107在排序后依旧排在第二个107的前面。
此时计数数组为,从前往后遍历原始数组中的元素。
第一次遇到107()时,107-101 = 6,,即第一个107在结果数组中的索引为5,即,排序后。
第二次遇到107()时,107-101 = 6,,即第二个107在结果数组中的索引为6,即,排序后。
以上就是计数排序算法的全部内容了,虽然它可以将排序算法的时间复杂度降低到,但是有两个前提需要满足:一是需要排序的元素必须是整数,二是排序元素的取值要在一定范围内,并且比较集中。只有这两个条件都满足,才能最大程度发挥计数排序的优势。
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/1082.html
