rsa算法加密和解密过程



题目👇

1. 编写求最大公因子的函数；
2. 编写求模逆的扩展欧几里得算法函数；
3. 编写rabin-miller素性检测算法函数；
4. 编写生成大素数的算法函数；
5. 编写生成RSA公私钥对的函数；
6. 编写RSA加密和解密函数；

思路分析👇

1.这里传进两个参数，我的思路是从较小的数中倒序遍历出最大公因子。

倒序的原因是你一旦找到某个公因子，那么它一定是最大的公因子，可以节省时间。

另外还要对异常作出相应处理，如果参数中有0存在就返回-1，如果参数中有负数存在就将其转化成正数来处理。

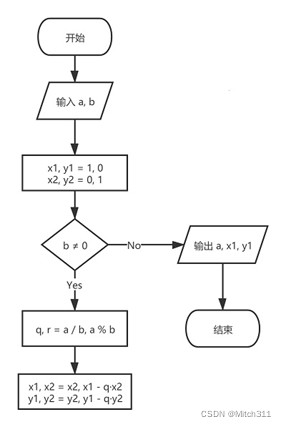
2.扩展欧几里得算法的具体步骤如下：

①若b≠0，使用带余除法，用b除以a得到余数r；否则转到第③步

②用b代替a，用r代替 b，重复第①步

③a的值就是最大公约数d

3.算法基于费马小定理，首先，根据Miller Rabin算法的过程：

假设需要判断的数是p，我们把p−1分解为2k∗t的形式；

当p是素数，有a2k∗t≡1(modp)，然后随机选择一个数a，计算出at(mod p)，让其不断的自乘，同时结合二次探测定理进行判断。

如果我们自乘后的数(modp)=1，但是之前的数(modp)≠±1，那么这个数就是合数(违背了二次探测定理)。

这样乘k次，最后得到的数就是ap−1，那么如果最后计算出的数不为1，这个数也是合数(费马小定理)。

4.生成指定比特位大小的随机数，利用刚才设计的Miller-Rabin算法来检验是否是素数，如果不是素数还需要重新生成一个随机数，如果是素数就返回即可。

5.过程如下：

①选取两个随机的指定比特位大小的素数p,q，这一步自然是由上一个RandomPrime()函数来生成。

②计算二者乘积 n=pq。

③随机选取选取参数e，并且测试是否满足(e,(p-1)(q-1))=1，不满足重新选取e，如满足则计算d满足ed+x(p-1)(q-1)=1，这一步使用扩展欧几里得算法来实现。

6.

①RSA的加密过程可以使用一个通式来表达

密文=明文^e mod n

也就是说RSA加密是对明文的e次方后除以n后求余数的过程。

从通式可知，只要知道e和n任何人都可以进行RSA加密了，所以说e、n是RSA加密的密钥，也就是说e和n的组合就是公钥，所以我们就用(e,n)来表示公钥=(e,n)

②RSA解密过程也可以使用一个通式来表达，类似加密

明文 = 密文^d mod n

也就是说对密文进行d次方后除以n的余数就是明文，这就是RSA解密过程。知道d和n就能进行解密密文了，所以d和n的组合就是私钥＝(d,n)

代码示例👇

版权声明：

本文来源网络，所有图片文章版权属于原作者，如有侵权，联系删除。

本文网址：https://www.mushiming.com/mjsbk/8284.html