原文链接
逻辑回归(Logistic Regression)是一种广泛用于分类任务的统计模型,特别适用于二元分类问题。尽管名称中带有“回归”,但逻辑回归主要用于分类。逻辑回归算法包含以下几个关键部分:线性回归与分类,Sigmoid 函数与决策边界,梯度下降与优化,正则化与缓解过拟合
分类问题和回归问题有一定的相似性,都是通过对数据集的学习来对未知结果进行预测,区别在于输出值不同。
既然分类问题和回归问题有一定的相似性,那么我们能不能在回归的基础上进行分类呢?
可以使用『线性回归+阈值』解决分类问题,也就是根据回归的函数按照一个阈值来一分为二,但是单纯地通过将线性拟合的输出值与某一个阈值进行比较,这种方法用于分类非常不稳定呢。
但是当我们单纯地使用线性回归来解决分类问题时,输出是一个未限定范围的连续值。这样做存在几个问题:
1.范围不固定:线性回归的输出可能是任何实数(比如 -∞ 到 +∞),这使得我们无法确定一个合理的阈值来判断输出 属于哪个类别。例如,可能得到一个极大的正值或负值,难以直接映射为0或1。
2.阈值选择困难:为了将连续值映射到离散类别(例如 0 和 1),我们通常需要一个判定阈值。如果线性回归的输出值不在一个固定的范围内,选择一个合适的阈值会变得非常困难,尤其是在处理极端值时。
我们是否可以把这个结果映射到一个固定大小的区间内(比如),进而判断。
当然可以,这就是逻辑回归做的事情,而其中用于对连续值压缩变换的函数叫做 Sigmoid 函数(也称 Logistic 函数,S函数)。
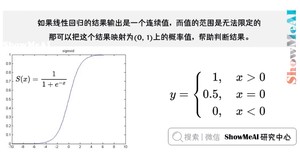
输出在之间。
上面见到了 Sigmoid 函数,下面我们来讲讲它和线性拟合的结合,如何能够完成分类问题,并且得到清晰可解释的分类器判定「决策边界」。决策边界就是分类器对于样本进行区分的边界。
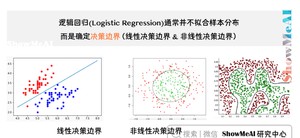
那么,逻辑回归是怎么得到决策边界的,它与 Sigmoid 函数又有什么关系呢?文中讲到了两类决策边界,线性和非线性。

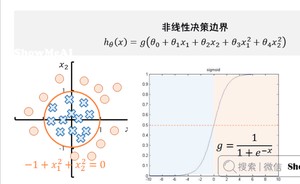
在这两张图中,右边的是我们的S函数,它将通过函数计算后的结果映射到了区间,那比如这里要做的就是二分类,就找0.5的那一条线,也就是在原函数中能将数据分成两组的函数,改变之类的参数,比如线性参数的例子里就是-3,1,1,以这几个参数做出来的函数就是决策边界,0.5则是判断边界。
前一部分的例子中,我们手动取了一些参数的取值,最后得到了决策边界。但大家显然可以看到,取不同的参数时,可以得到不同的决策边界。
哪一条决策边界是最好的呢?我们需要定义一个能量化衡量模型好坏的函数——损失函数(有时候也叫做「目标函数」或者「代价函数」)。我们的目标是使得损失函数最小化。总不能一直手动去取参数。
我们如何衡量预测值和标准答案之间的差异呢?最简单直接的方式是数学中的均方误差
均方误差损失(MSE)在回归问题损失定义与优化中广泛应用,但是在逻辑回归问题中不太适用。 因为Sigmoid 函数的变换使得我们最终得到损失函数曲线如下图所示,是非常不光滑凹凸不平的.
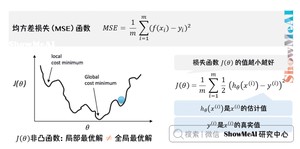
我们希望损失函数如下的凸函数。凸优化问题中,局部最优解同时也是全局最优解
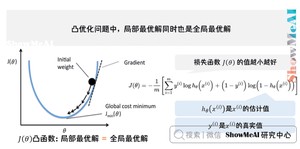
在逻辑回归模型场景下,我们会改用对数损失函数(二元交叉熵损失),这个损失函数同样能很好地衡量参数好坏,又能保证凸函数的特性。对数损失函数的公式如下:
其中表示的可以说是根据这个h函数预测的样本值,表示样本取值,在其为正样本时取值为1,负样本时取值为0,正负样本就是我们之前说的分的那两类,比如正常邮件是正样本,垃圾邮件是负样本,我们分这两种情况来看看:
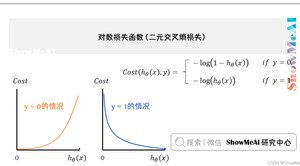
:样本为负样本时,若接近1(预测值为正样本),那么值就很大,也就是对应的惩罚也越大
:样本为正样本时,若接近0(预测值为负样本),那么值就很大,也就是对应的惩罚也越大
通过惩罚大小就可以判断出参数好坏了。
损失函数可以用于衡量模型参数好坏,但我们还需要一些优化方法找到最佳的参数(使得当前的损失函数值最小)。最常见的算法之一是「梯度下降法」,逐步迭代减小损失函数(在凸函数场景下非常容易使用)。如同下山,找准方向(斜率),每次迈进一小步,直至山底。
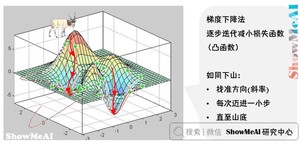
梯度下降(Gradient Descent)法,是一个一阶最优化算法,通常也称为最速下降法。要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索。
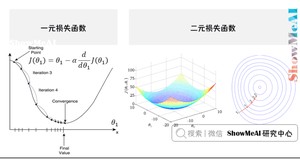
上图中,称为学习率(learning rate),直观的意义是,在函数向极小值方向前进时每步所走的步长。太大一般会错过极小值,太小会导致迭代次数过多。
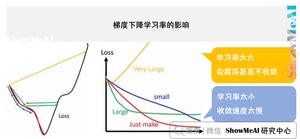
进一步学习梯度算法
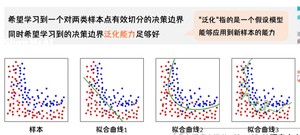
曲线3就是过拟合,学的太死板了也就是,那咋办呢?
过拟合的一种处理方式是正则化,我们通过对损失函数添加正则化项,可以约束参数的搜索空间,从而保证拟合的决策边界并不会抖动非常厉害。如下图为对数损失函数中加入正则化项(这里是一个L2正则化项)
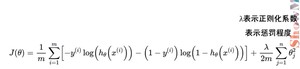
在损失函数后面的那一项就是L2正则化项,L2 正则化可以看作是对参数空间内欧氏距离的惩罚。其几何效果是缩小所有参数,使它们更加接近原点,从而降低模型复杂度,会惩罚较大的参数值,但不会直接将它们缩减为零。这种“平滑”的惩罚方式促使模型将所有特征的权重均衡分配,从而减少过拟合。
我们依然可以采用梯度下降对加正则化项的损失函数进行优化。
下面使用了scikit-learn提供的乳腺癌数据集作为示例数据集
结果如下
我们再用python构建一个原生的算法模型,用到了交叉损失函数和正则化
下面是结果
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/7115.html
