2020-05-22
所有背包问题实现的例子都是下面这张图
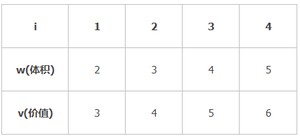
01背包实现之——穷举法:
1.我的难点:
(1)在用穷举法实现代码的时候,我自己做的时候认为最难的就是怎么将那么多种情况表示出来,一开开始想用for循环进行多次嵌套,但是太麻烦,而且还需要不断的进行各种标记。我现在的水平实在太菜,然后就在一篇博文中看到一个特别巧妙的枚举算法,如下所示:
虽然我现在也不知道为什么会这样,但是确实是个很好的规律,找到这个规律后,就可以很轻松的自己写出各种排列情况,以后遇到排列的问题,就用这个方法。语言不好描述,上图片演示(是歪的,凑活看吧。。。):
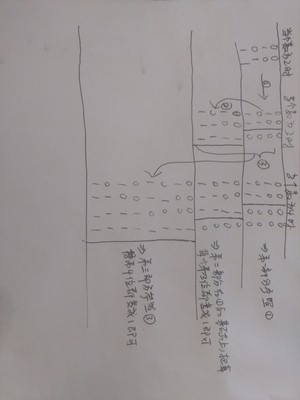
(2)算法思想:
x[i]的值为0/1,即选或者不选
w[i]的值表示商品i的重量
v[i]的值表示商品的价值
所以这个算法最核心的公式就是
tw=x[1]*w[1]+x[2]*w[2]+.......+x[n]*w[n]
tv=x[1]*w[1]+x[2]*v[2]+......+x[n]*v[n]
tv1:用于存储当前最优解
limit:背包容量
如果 tw<limit&&tv>tv1 则可以找到最优解
2.代码实现(借鉴博文)
3.运行结果: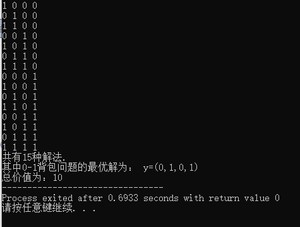
4.复杂度分析
n个物品的话,就有2^n-1种解,所以其时间复杂度为O(2^n)
01背包问题之——贪心算法:
1.算法思路:
取单位价值量最大的那个物品先装入背包。所以还算好实现,得到每一个物品的价值量之后,查找最大的价值量的坐标,判断这个坐标额物品体积是否小于背包的容量,若小于,则装入背包。否则,继续循环。
2.代码实现 法一:
将得到的每个物品的价值量进行排序,得到一个递减序列。
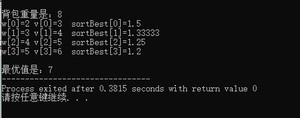
代码实现 法二:
没有对每个商品的价值量进行排序,直接查找当前价值量的最大值,判断其是否能够装入背包,若能,直接装入,令当前价值量为0,继续寻找第二大价值量,不断循环即可。代码如下:
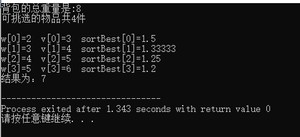
3.遇到的困难
就是,当得到的价值量的包含小数时,而且刚好就靠小数部分区分大小时(比如1.5 ,1.33,)。c++正常输出的结果都是整数。
解决办法就是,将每个物品的价值量(3.0,4.0)和背包重量(2.0,3.0)都变float类型,注意定义的时候,也需要定义为float类型
4.复杂度:
时间复杂度:O(n)
01背包问题之——动态规划
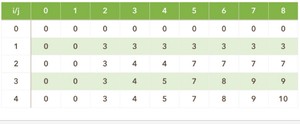
1.算法思想
最重要的就是寻找递推关系式:
定义V[i,j]:当背包容量为j时,前i个物品最佳组合对应的值。
递推关系:
(1)当背包的容量不允许装入第i件物品时,和前一个物品装入背包一样。即 :V[i][j]=V[i-1][j]
(2)当背包的容积可以装入第i件物品时,分两种情况,A装入第i件物品不是最优,还不如不装。B装入第i件物品是最优。即:V[i][j]=max(V[i-1][j],V[i][j-w[i]]+v[i])
2.代码实现:
下面是带上回溯找出解的组成的代码:
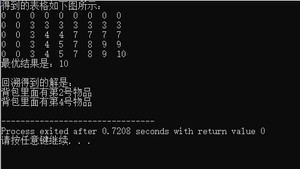
3.复杂度
时间复杂度:
O(物体个数*背包容积)=O(number*capacity)
空间复杂度:
用二维表实现的,所以和时间复杂度一样。
O(物体个数*背包容积)=O(number*capacity)
01背包之——递归
1.
递归法思路很单一,也是在递归方程的基础上,将其改造为可以递归的方式
2.代码演示
3.我的难点:
因为是递归,所以其最大的缺点就是重复计算,所以如果我想查找他的解是什么,不容易查找。因为如果你进行标记的话,因为会重复计算,所以标记的话,标记也是不停的会变。所以我也不知道怎么解决。
4.复杂度:
O(2^n)
01背包之——回溯
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/6339.html
