真、假正例和负例用于计算一些有用的 来评估模型。哪些评估指标最为重要 具体有意义取决于具体模型和具体任务、 以及数据集是平衡的,还是 不平衡。
此部分中的所有指标都是按单个固定阈值计算得出的, 并在阈值变化时更改。用户经常会调整 以优化其中某个指标。
准确率是 正确的分类(无论正面还是负面)。时间是 从数学上定义为:
[ ext{Accuracy} = frac{ ext{correct classifications}}{ ext{total classifications}} = frac{TP+TN}{TP+TN+FP+FN}]
在垃圾邮件分类示例中,准确率衡量在垃圾邮件分类中 正确分类的电子邮件。
完美的模型应该没有假正例和假负例 因此准确率为 1.0 或 100%。
因为它综合了 混淆矩阵 (TP、FP、TN、FN), 因为两个类别的样本数量相似,所以准确率可以 作为模型质量的粗略衡量标准。因此, 用于通用模型或未指定模型的默认评估指标 执行通用任务或未指定任务。
但是,如果数据集不均衡, 或者,一种错误(FN 或 FP)比另一种造成的代价更高, 与在大多数实际应用中一样,最好针对 其他指标
对于高度不均衡的数据集,其中一个类别很少出现,例如 1% 一个预测模型在 100% 的时间内预测为负值的模型, 也没什么用处。
真正例率 (TPR),即满足以下条件的所有实际正例所占的比例 被正确分类为正类别,也称为 召回率。
召回率从数学上定义为:
[ ext{Recall (or TPR)} = frac{ ext{correctly classified actual positives}}{ ext{all actual positives}} = frac{TP}{TP+FN}]
假负例是指被错误分类为负例的实际正例, 是它们出现在分母中的原因。在垃圾邮件分类示例中, 召回率衡量的是正确分类为垃圾邮件的电子邮件所占的比例 垃圾内容。因此,召回率的另一个名称是“检测概率”: 回答“此 模型?”
假设的完美模型没有假负例,因此 召回率 (TPR) 为 1.0,即 100% 的检测率。
在一个不均衡的数据集内,实际正类别的数量 例如,共计 1-2 个样本,则召回率会不太有意义,实用性也较低 作为指标
假正例率 (FPR) 是错误分类的所有实际否定关键字所占的比例 也称为“误报概率”。时间是 从数学上定义为:
[ ext{FPR} = frac{ ext{incorrectly classified actual negatives}} { ext{all actual negatives}} = frac{FP}{FP+TN}]
假正例是指分类有误的实际负例,这就是 它们出现在分母中。在垃圾邮件分类示例中,FPR 将 被错误分类为垃圾邮件的合法电子邮件所占的比例,或者 模型的假警报率。
完美的模型应该没有假正例,因此 FPR 为 0.0, 也就是说,误报率为 0%。
在一个不均衡的数据集内,实际负例的数量 假设总共有 1-2 个样本,则 FPR 没什么意义,实用性也没那么高 作为指标
精确率 是模型的所有正分类所占的比例, 是正值。其在数学上定义为:
[ ext{Precision} = frac{ ext{correctly classified actual positives}} { ext{everything classified as positive}} = frac{TP}{TP+FP}]
在垃圾邮件分类示例中,精确率测量的是电子邮件的比例 被归类为垃圾内容,但实际上是垃圾内容。
假设的完美模型没有假正例,因此 精度为 1.0。
在一个不均衡的数据集内,实际正类别的数量 假设样本总数为 1-2 个,那么精确率没那么有意义,实用性也没那么高 作为指标
精确率会随着假正例的减少而提高,而召回率则会随着假正例的减少而提高 假负例降低。但如上一部分所示,增加 分类阈值往往会减少假正例的数量, 可增加假负例的数量,而降低阈值可 产生相反的效果。因此,精确率和召回率通常显示出 改善其中一个关系会让另一个恶化。
亲自尝试:
NaN,即“非数字”,在除以 0 时显示 与这些指标中的任何一个相关联例如,当 TP 和 FP 均为 0 时, 精确率公式的分母为 0,因此得出了 NaN。虽然 在某些情况下,NaN 可能表示完美的性能, 也来自实际模型。 毫无用处。例如,从未预测正例的模型将具有 0 TP 0 FPS,因此计算其精度时将产生 NaN。
您在评估模型时选择优先考虑的指标和 阈值的选择依据是 AI 技术的成本、收益和风险, 具体问题。在垃圾邮件分类示例中, 优先考虑召回率、捕获所有垃圾邮件或精确率, 并尝试确保带有垃圾邮件标签的电子邮件确实是垃圾邮件, 两者之间的平衡,高于某个最低准确度水平。
用作模型的粗略指标 均衡数据集的训练进度/收敛情况。
对于模型性能,请仅与其他指标结合使用。
避免数据集不均衡。请考虑使用其他指标。
召回率(真正例率) 适用于假负例较多的情况 开销要比假正例高。 假正例率 出现假正例的情况 比假负例的开销要大。 精确率 在对以下业务非常重要时使用 提高正向预测的准确性。
F1 得分是调和平均值 (a 一种平均值)的精确率和召回率。
其数学公式由以下公式计算得出:
该指标平衡了精确率和召回率的重要性, 准确率比准确率更高。如果精确率为 且召回率均为 1.0,F1 也有完美得分 为 1.0。从更广泛的意义上来说,当精确率和召回率值相近时,F1 将 接近其价值。如果精确率和召回率相差很大,F1 将 与哪个指标更差的指标相似。
上一部分介绍了一组模型指标,这些指标均以 单个分类阈值。但如果您想评估 模型质量在所有可能的阈值下,则需要不同的工具。
ROC 曲线 是模型在所有阈值上的表现的可视化表示。 这个长版名称(即接收器操作特征) 来自二战雷达侦测工具
ROC 曲线的绘制方法是计算真正例率 (TPR) 和假正例率 (FPR) 值(在实践中, 然后绘制 FPR 的 TPR 图表。完美的模特 在某些阈值下,TPR 为 1.0, FPR 为 0.0, 都表示为 (0, 1)(如果所有其他阈值均被忽略),或者出现以下情况:

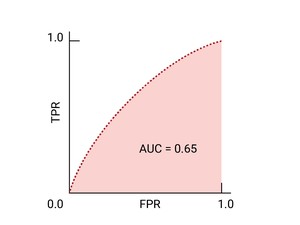
ROC 曲线下面积 (AUC) 表示模型的概率, 如果给定一个随机选择的正类别和负类别样本, 正值将大于负值。
上述完美模型包含一个边长为 1 的正方形, 曲线下面积 (AUC) 为 1.0。也就是说,有 100% 的可能性 模型会正确地将随机选择的正例排列在 随机选择的负例。换句话说,如果观察 AUC 给出了模型将 随机选择的圆圈右侧的平方,与 阈值。

具体而言,使用 AUC 的垃圾邮件分类器 则随机分配垃圾邮件的概率始终较高, 随机生成合法电子邮件每个单元的实际分类 取决于您选择的阈值。
对于二元分类器来说,一个模型与随机猜测或 抛硬币的 ROC,它是一条从 (0,0) 到 (1,1) 的对角线。曲线下面积为 0.5,表示对某个随机正例进行排名的概率为 50%, 反例。
在垃圾邮件分类器示例中,AUC 为 0.5 的垃圾邮件分类器将 随机发送垃圾邮件的概率要高于随机发送的垃圾邮件 合法电子邮件只占一半的时间。

AUC 和 ROC 非常适合在数据集大致如下的情况下比较模型 不同类别之间的平衡。当数据集不平衡时,精确率与召回率 以及这些曲线下方区域的面积可能会提供 直观呈现模型性能精确率/召回率曲线由 y 轴的精确率和 x 轴的召回率 阈值。

曲线下面积是一个非常有用的指标,用于比较两个不同模型 只要数据集大致均衡即可。(请参阅精确率与召回率曲线, 针对不平衡的数据集。)下方是较大区域 那么曲线通常效果最佳

ROC 曲线上最接近 (0,1) 的点表示 指定模型表现最佳的阈值。正如 阈值、 混淆矩阵 和 指标选择和权衡 选择阈值取决于对应用而言最重要的指标 具体用例。请考虑以下要点 A、B 和 C 示意图,每个选项代表一个阈值:

如果误报(误报)的代价很高, 即使 TPR 。相反,如果假正例费用低廉, (错失的真正例)代价很高,C 点的阈值 可以最大限度提高 TPR,可能更合适。如果费用大致相等,请确定 B 点 可在 TPR 和 FPR 之间实现最佳平衡。
以下是我们之前看到的数据的 ROC 曲线:








试想一下,在这样一种情况下,最好让一些垃圾邮件进入 将对业务至关重要的电子邮件发送到垃圾邮件文件夹。您已 针对这种情况,我们训练了一个垃圾邮件分类器, 而负类别则不是垃圾邮件。 以下哪些要点 ROC 曲线上的任何数据是否更合适?

正如我们在 线性回归 计算 预测偏差 可以标记模型或训练数据中存在的问题, 。
预测偏差是指一个模型 预测 求平均值, 标准答案标签 数据。使用数据集训练的模型 其中 5% 的电子邮件是垃圾邮件,平均而言, 被归类为垃圾邮件的电子邮件。也就是说, 标准答案数据集的概率为 0.05,那么模型预测的平均值应为 也为 0.05。在这种情况下,模型的预测偏差为零。/ 那么模型可能仍存在其他问题。
如果模型有 50% 的时间预测电子邮件是垃圾邮件,那么 训练数据集存在问题,模型的新数据集 模型本身。不限 二者之间的显著差异表明模型 某些预测偏差。
导致预测偏差的原因可能是:
- 数据中的偏差或噪声,包括训练集的偏差抽样
- 正则化过于强烈,意味着模型过度简化, 必要的复杂性
- 模型训练流水线中的 bug
- 提供给模型的特征集不足以完成任务
多类别分类可视为 二元分类 分为两类以上。如果每个样本只能 那么分类问题就可以 二元分类问题,其中一个类别包含一个 另一个类包含所有其他类汇总在一起。 然后,可以对每个原始类别重复此过程。
例如,在一个三类别多类别分类问题中, 其中,使用标签 A、B 和 C,则可以将问题转换为两个单独的二元分类。 问题。首先,您可以创建一个二元分类器,用于对样本进行分类 标签为 A+B 和标签 C。然后,您可以创建 二元分类器,用于对标记为 A+B 的样本进行重新分类 标签 A 和标签 B。
一个多类别问题的例子是手写分类器, 手写数字的图像,并确定代表哪个数字 0-9。
如果课程成员资格不是排他性的,也就是说, 这种模型就称为多标签分类 问题。
在以下练习中,您将训练一个二元分类器,以将两个 并计算相关指标。
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/5973.html
