光线和三角形求交 - 穆世明博客

时间又过去了近两年，兜兜转转又回到了设备圈子。现在看看先前的想法似乎还是带着些书生气。又跳槽了一次，从纯技术岗到了基础管理岗，又到了项目管理岗，想法或多或少有些更新，不一定全对，看官们随便看看，大可以一笑置之。

除了少数几个半导体国产巨头，AMEC，ACM，NAURA，etc。大多数海外设备玩家在国内都是SSC，sales & service是核心岗位。但凡有野心（个人觉得是个中性偏褒义词），在从事若干年后的技术工作，出于职业生涯考量，还是很有必要转型的。当然天赋型选手除外。但是在从事技术工作的同时，个人觉得真的非常有必要培养自己的business sense，同时包括但不限于向上/向下管理能力，沟通技能等等。（现在深刻感受到自己都会点，但似乎又啥都不到位的痛）见过不少大佬，尤其最近的项目和几个O交集比较多，真切感受到了如新手进入大佬村。

说到底，FEI，JEOL都是一份工作，都是一份外企SSC的工作，都是为了卖设备的工作。不要想得太高大上，也不要想得太easy。不然心里容易失衡，也容易崩溃。多学习多读书多沟通。最近重新开始看看学术论文，也打算看看先进封装，Litho和PMP的书，与诸君共勉。

-------------------------------

作为前FEI时代最后一位Application（勿抬杠，之后入职的都是签的大赛默飞），某半年内大陆地区唯二的Application（勿抬杠，真的加老板也就3个人），我觉得我还是可以简单聊聊这个问题的。

首先入职FEI，或者赛默飞MSD部门，其实内推得到offer或者面试机会会远高于直接投简历。倒不是说潜规则，而是说电镜技术这个东西，很难靠面试和笔试来断定，有人背书总归会更靠谱些。所以在workshop或者training的过程中，多和设备公司的FSE和FAE交流，或者和负责设备的老师也行，后续的机会会多很多。

再者呢，我可能想适当反驳一下前面同学的一部分观点。说到底，离开学校和科研圈，business is business，薪水是和你能bring in多少business直接挂钩的。这也是为什么大多数公司销售部门是绝对的权力部门，大佬也大多数出自这个部门。所以薪水只能说不高，但是合理。学术做的好不代表能协助卖出更多机台，文章发的好不代表能协助卖出更多机台。说到底博士学位，高引paper在手，只是拿到了入场券而已。演讲能力，随机应变能力（主要是demo过程中），沟通能力（包括技术沟通），以及商业敏感度，乃至市场分析能力都是必须的。

至于说个人发展，我们可以把眼界放得更宽广些，半导体行业，生物制药行业其实和电镜圈都有一定的overlap。或者说如果不考虑行业的overlap，其实职能的overlap就更多了。销售就可以略过不提，哪哪都需要。作为一名已经离职的App，我和我的小伙伴们广泛分布在高校，半导体，生物制药以及其他友商，科研岗位，管理岗位，市场岗位都有。专业技能是狭窄的，但是我一直认同一句话（来自某爆款微信推文），博士学位证明了你拥有通过努力和学习，胜任所有岗位和工作类型的能力。

最后说说生活，维修、销售和产品市场经理就不提了，我在入职后的前半年就见了我老板3回。应用出差虽说算是少的了，但是绝对不是40%这种比例（除非按自然日算）。单纯算工作日的话，肯定到70%了，管够你刷上东航金卡，以及两三个白金会籍了。生活和工作可以平衡就不要想了，单身的连女朋友都没法谈，好么（我爱我老婆，真心的）。想不想体验下36小时横跨赤道和10个时区；想不想体验下前首富那样1天2国3城。大赛默飞，你值得拥有！

最后总结一下，如果对高频出差不排斥，身体不算差，嘴巴不算笨，技术不算怂，薪资不奢求，我觉得还是蛮好的。有任意一项不满足，嗯…还是洗洗睡了吧。

光栅化：光源-->物体表面-->人眼

光线追踪：光源-->物体表面....xN-->人眼

至于它为什么叫“光栅化”呢？主要是因为默认光线只反射一次，从而可以把反射计算整个放在二维图像空间里做，二维图像就是所谓的“光栅”

一个好的光栅（误）可以包含很多特征信息：颜色 (hue)、对比度 (contrast)、朝向 (orientation)、时间频率 (time frequency, c/s 或 °/s)、空间频率（spatial frequency, c/°）、位移速度 (drift rate, °/s)、曲率。

低速运动光栅，著名的barberpole illusion，其实也是移动光栅带来的视觉效应

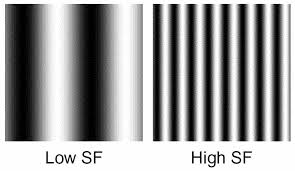
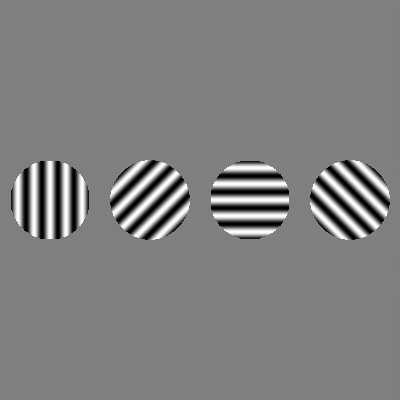
为什么这些信息对于研究视知觉很重要呢？

视觉皮层中，神经元选择性地对视觉信息的某些特征进行加工，包括上述所有的特征信息。

以朝向信息为例，一个神经元对于0-360°的线条方向是存在tuning function的，对于某一特定朝向的响应最为强烈，偏离该朝向的则顺次递减。下图该神经元响应最强烈的朝向是90°，但对于其他神经元，可能就是45°、135°了。

其他特征的加工也有类似的tuning function，比如一个神经元对红色最敏感，或者由几个神经元组成的更大区域对红色最敏感。

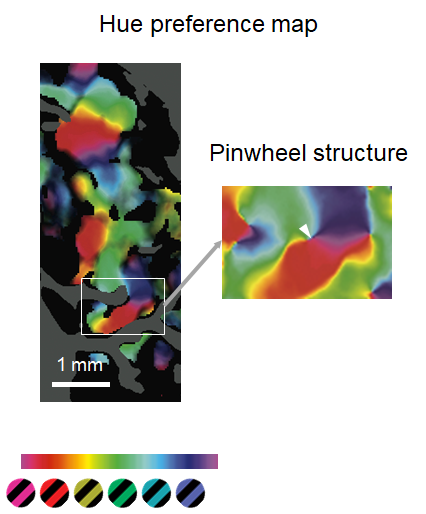
其他特征在视皮层中的tuning mapping也被研究得很透彻了，在此不一一列举。

所以说，比起真实场景的照片，光栅是一种能够灵活调节、有效激发、信噪比高的视觉刺激，在研究视皮层的感知能力和高级认知皮层的视觉信息加工时都会用到。

而且，光栅在响应敏感度 (responsitivity-sensitivity) 上效果比使用单个bar要好（Albrecht, D. G. et. al, 1980)。

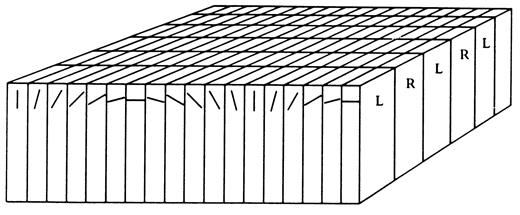
初级视皮层V1中的column结构，窄带（thin stripe）为对朝向信息的选择性，宽带（thick stripe）为对左右眼信息的选择性。

腹侧视觉通路加工层级示意图。初级视觉皮层处理比较基础的视觉刺激特征，高级视皮层相对复杂，下颞叶作为腹侧视觉通路终端则可以处理人脸、肢体等更复杂的物体特征。

刚开始看题主的标题，还以为是用cpu端做光栅化，进来看发现是用CS做光栅化。那么既然GPU上有专门光栅化的硬件单元，为什么要占用通用流处理器来处理光栅化呢？第一种情况就是没办法使用raster engine，比如使用visibility buffer pipeline，就需要自己处理光栅化。另一种情况就是raster engine做的不好，raster engine是硬编码，它的实现目标是满足大部分情况下性能最优，对于某些极端情况下raster engine处理的并不好，比如对于像素占用小于4的三角面片。所以对于软光栅化，并不是引擎层面做不到，而是引擎需不需要使用软光栅化。你提的这个问题其实牵扯了一个比较大的问题就是GPU到底有没有必要再用专用的raster engine来做光栅化了。MS已经统一了raster engine之前的渲染流程，那么横在中间的raster engine是不是也可以去掉了，到底是统一好还是使用专用的硬件好，这个不是游戏公司和操作系统公司说的算，要看GPU厂商的态度，从目前GPU的架构演变来说，通用化是大势所趋，因为GPU已经不再只服务渲染了，它希望将自己定位在AI上，而AI的市场要远远大于图形渲染。从硬件成本来说raster engine很有可能会被替换成更多的通用流处理器，这样对AI更友好，对图形渲染可能不是最优解但是也不赖。以后的GPU就是并行的通用处理器，不再是图形显卡了。

一、光栅衍射效果的解释：

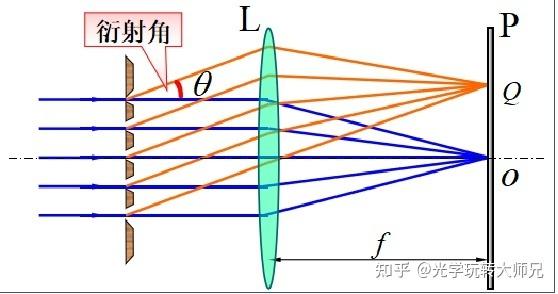
平行光垂直照射在衍射光栅上，每个透光缝产生单缝衍射，各个透光缝之间形成多光干涉，透射光栅的衍射条纹是衍射与干涉的合成效果，当相邻单缝出射光在某一衍射角方向的光程差等于波长的整数倍时，即

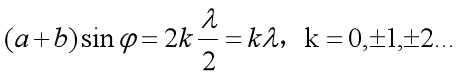
这些光经过透镜L汇聚后在屏幕上增强，形成明条纹，上式称为光栅公式。

总结来说：光栅衍射效果=多缝干涉+单缝衍射的综合效果。

二、基于光栅原理，解释光栅缺级产生原理：

若衍射光栅的某一级明条纹（k级）与单缝衍射的某一暗纹（k级）出现在同一衍射角φ，这时光栅衍射的第k级明条纹不再产生，变为缺级，由光栅公式和单缝衍射的暗纹公式相除得出光栅缺级公式：

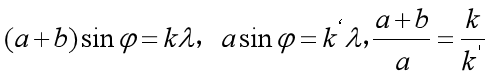
考虑到k和k‘均为整数，所以当（a+b）/a为整数比时，会产生缺级现象，缺少的主极大级次为：

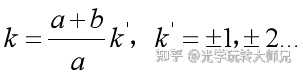
光栅其实是多缝干涉，而双缝干涉实验是双缝，理论上双缝干涉也是有单缝衍射的，只要满足上述缺级条件，是会出现缺级的。

三、补充一个结论：

干涉中不一定有衍射，但衍射中一定有干涉；

我对头戴显示设备的期望是能折叠装进常见的眼镜盒（毕竟很多人会戴眼镜，包里装眼镜盒）、价格不高于主流智能手机、可提供AR功能以便直观的导航与辅助工作、有可更换电池并提供节能模式确保合力续航。操作上提供空中手势、动作捕捉、眼动追踪、交互手套等方式。这样才便于普及才有真正的元宇宙。

注意头戴VR/AR不可能取代平板和笔记本，而是类似蓝牙耳机的外设。本身不应当承担重度计算任务，否则体积重量、功耗发热都得爆炸没法用。

5年时间啊，还不够！

VR/AR/XR设备微型化有一个前提：

电池技术的一次全新的革命。

就拿VR头显来说：

VR设备使用的电池有一个很大的特点，那就是电池能够有一定的弯曲度或者有一定的薄度。

戴在头上的设备肯定是越轻越好。

所以这也就决定了VR电池一般都是使用异形的电池。

由于异形电池是可以做成不同的外形，

一般的电池如镍氢电池等由于电解质是液体的限制就注定没法进行外形可塑化。

而聚合物电池的电解质属于胶态，可以组成不同形态，是异形电池的最佳选择。

所以VR眼镜使用的电池大部分都是异形锂聚合物电池，

这由VR眼镜设备的实际使用情况和程度决定的。

个人觉得VR设备的进化方向，应该是马斯克正在搞的脑机接口，

人只需要躺着就行了，就可以进入元宇宙体验。

或者像美剧《边缘世界》里提到的，共享神经系统也是一个不错的思路，

弄一个边缘人，通过远程的方式去操作，同时又能获得真实无比的体验。

真正在未来一段时间内，能替代掉笔记本和平板的。

反倒是AR眼镜可能会概率大一些，虽然现在AR眼镜还在投屏器阶段徘徊，

但未来技术的迭代和更新，到底能做成什么样子，

还是很有想象力的，坐等苹果出AR眼镜，看看设计交互体验如何。

欢迎关注我，@专注的小白

数码情报员 / IT产品专家 / 阅读爱好者

擅长创作领域：数码科技 | 产品分析 | 深度阅读

让我们一起，专注品质，品味生活！

专注的小白

近几十年来，产品开发越来越受到设计和人体工程学的影响。复杂的功能被挤进超小尺寸的包装，越来越多的应用由电池供电，而且可移动。作为消费者，我们乐见这种改变；但作为开发工程师，它对我们日常工作产生的影响越来越明显。

传感器系统的研发也深受此影响：曾经足以连接商用编码器，现在通常需要根据给定的机械限制设计特殊的传感器配置。

MPS MagAlpha位置传感器系列的新成员，MA782 此时应运而生。

MA782采用了MPS专有的SpinAxisTM 技术，该技术可实现完整角度传感器的单片集成，内部传感器前端横截面积仅占1平方毫米（见图1）。这项技术与其他方法形成鲜明对比，后者通常需要将单独的传感器前端（例如磁阻）与处理单元（例如内插器）相结合。

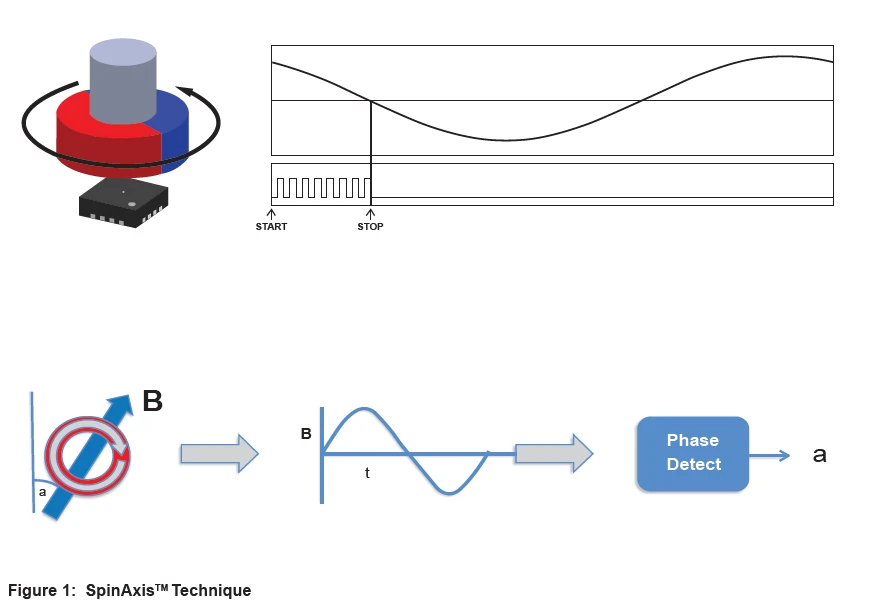
典型的IC封装采用沿硅芯片边缘延伸的引线键合连接，将焊盘连接到引线框架。而现代倒装芯片技术则倒装芯片，并将焊盘通过焊料凸点直接连接到引线框架，从而减少了圆周边缘。利用这项技术， MA782可以将占板面积缩小至2mmx2mm，比MPS其他MagAlpha传感器外形尺寸还要小50％以上（见图2）。

MPS SpinAxisTM 技术的另一个优势便是MA782可以直接正对着旋转磁体的中心（轴端）放置，也可以侧向移位（轴侧）放置，甚至可以正交于磁体平面边缘（正交于轴侧）放置（见图3）。它适用于直径磁体、环形磁体或多极环形磁体等多种类型的磁体。这种传感器位置的通用性足以应对非常严苛的限制。

继续阅读 >>>请点击下方链接进入MPS官网查看全文：

世界上超小的绝对角度位置编码器芯片（IC Encoder™）- MA782

文章转载自公众号【字节跳动SYS Tech】。原文链接点击：3D渲染——光栅化渲染原理解析 | 文末抽奖、热招职位

随着技术的发展，基于 GPU 的渲染技术得到了广泛应用，日常生活中常见的 3D 动画和游戏都是通过计算机渲染技术来实现。当前主要的 3D 渲染模型包括光栅化渲染和光线追踪两大类，本文主要围绕光栅化渲染进行介绍，描述了简单场景下3D渲染过程，主要帮助读者了解基于光栅化的 3D 渲染原理及过程。本文为系列文章，并在下一篇系列文章中以 Intel Gen12 为例，讲述 GPU 一些基本硬件单元及如何利用硬件加速渲染过程。希望通过这种软件计算 + 硬件实现的方式，让大家了解 GPU 3D 渲染原理及过程。

在开始正式的介绍前，有以下几点说明：

在渲染过程中，涉及到向量、矩阵等数学知识不再阐述。在后面用到的时候会有提及
文中选择了一个简单的模型场景，过程也尽可能简化。旨在重点讲述光栅化流程，便于读者理解
推荐课程 GAMES101，文章后面用到的一些图片出自该课件

图0 是光栅化的一个简易图，其中光栅化主要完成以下两个功能：

将几何图元（三角形/多边形）投影到屏幕上
将投影之后的图元分解成片段

下文开始举例说明光栅化过程，为了更简单的说明光栅化，我们选用相对简单的模型，在三维空间中存在两个三角形，其中三角形1 三个顶点坐标分别为(-2, 0, -2)、(2, 0, -2)、(0, 2, -2)，三角形2 三个顶点坐标分别为(-1, 0.5, -20)、(2.5, 1, -20)、(3, -1.5, -20)，之所以后面三角形 z 绝对值比较大，是为了后面观察透视投影近大远小的效果。在模型中，除了被观察物体，还需要确认观察点的位置，这里将相机放在位置(0, 0, 0)，观察方向是 z 轴负方向（z-），向上向量为 y 轴正向（y+)。模型如图1所示：

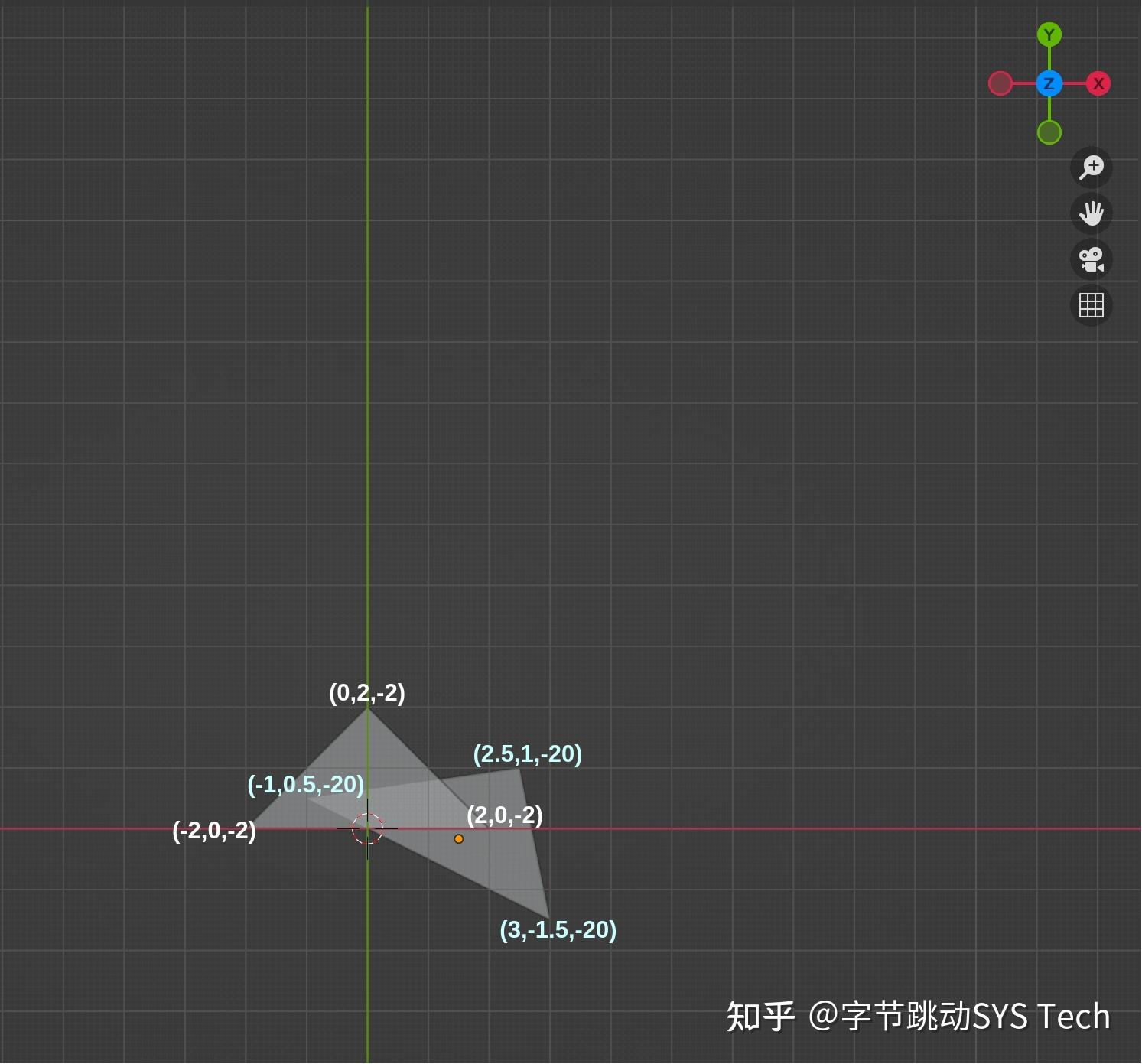
物体和相机的位置已经放好了，那么我们接下来要做的就是要将相机实际看到的内容最终显示到屏幕上。模型是三维的，而最终的成像是二维，所以这其中必然要有投影操作。

先来看一下透视投影和正交投影的效果图：

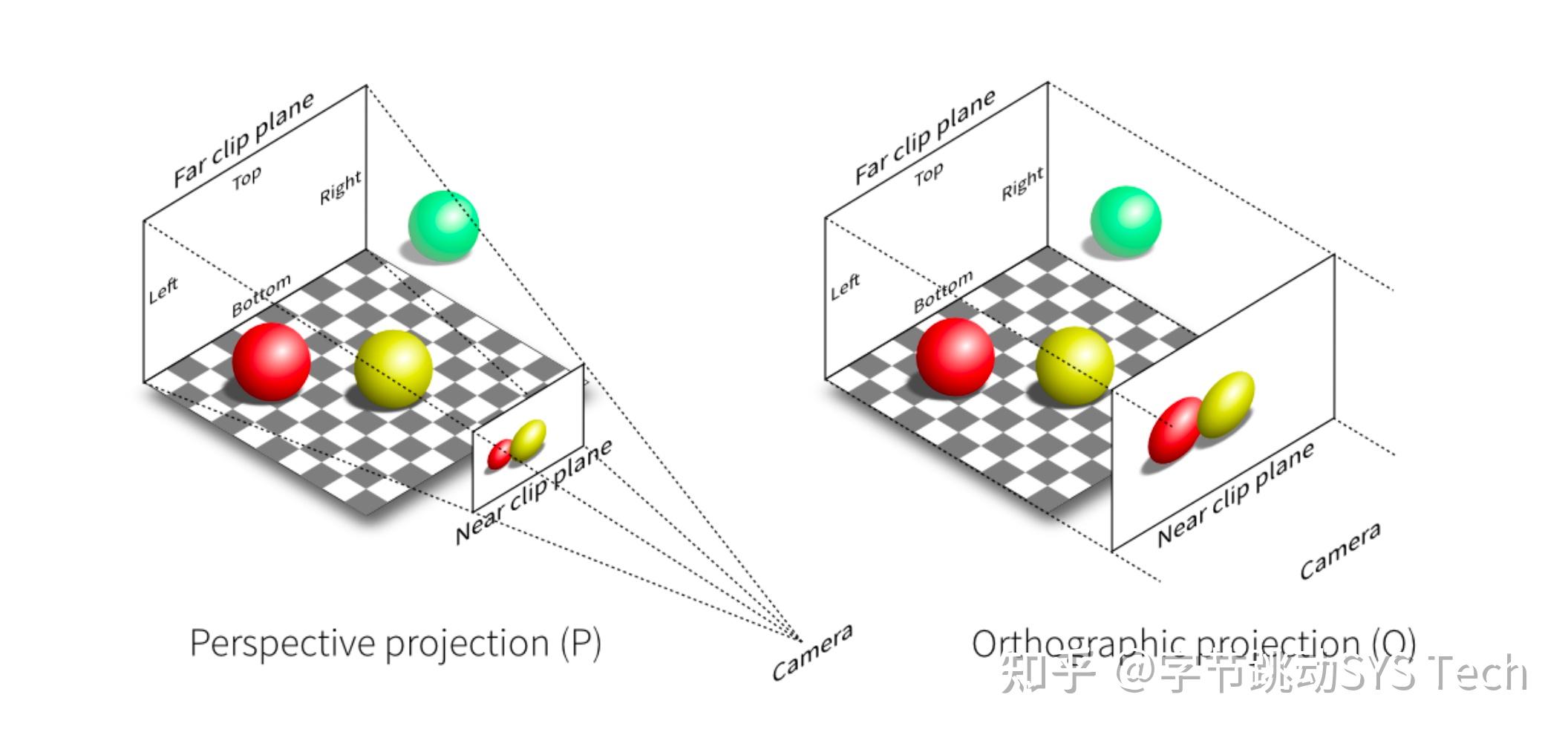
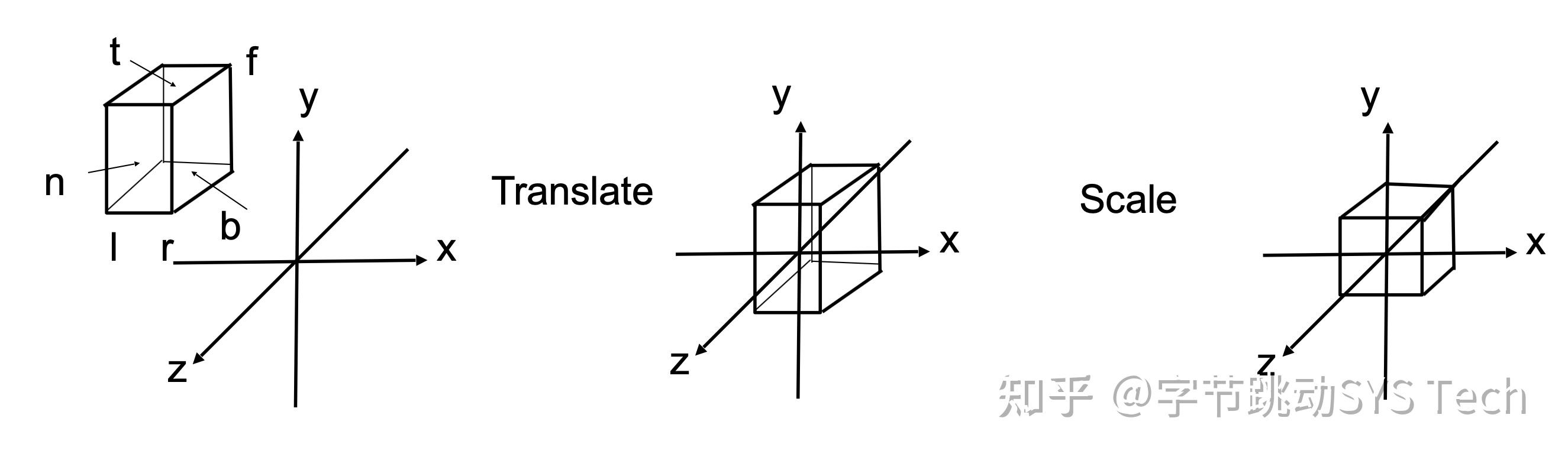
对比正交投影和透视投影效果可以发现，透视投影的结果会有近大远小的效果，而正交投影不会。正交投影中，以平行线投射方式投影，在工程制图等场景应用广泛。透视投影这种近大远小的效果和人眼成像效果基本一致，后面主要针对透视投影讲解。也正是因为这种效果，才有了"道理我都懂，可是为什么鸽子这么大"这个梗。绿色的球在视野之外，会被裁剪掉。透视投影本质就是对一个平截头体及平截头体里的物体（图2左半边虚线内部分，包含红球和黄球）做变换，这时候平截头体会被压成长方体(图3-1)，变换后的物体也包含在这个长方体中，最终长方体标准化生成[-1, 1] ^ 3标准正方体(图3-2)，然后再针对[x, y]平面做投影，投影过程中z轴作为深度覆盖参考。

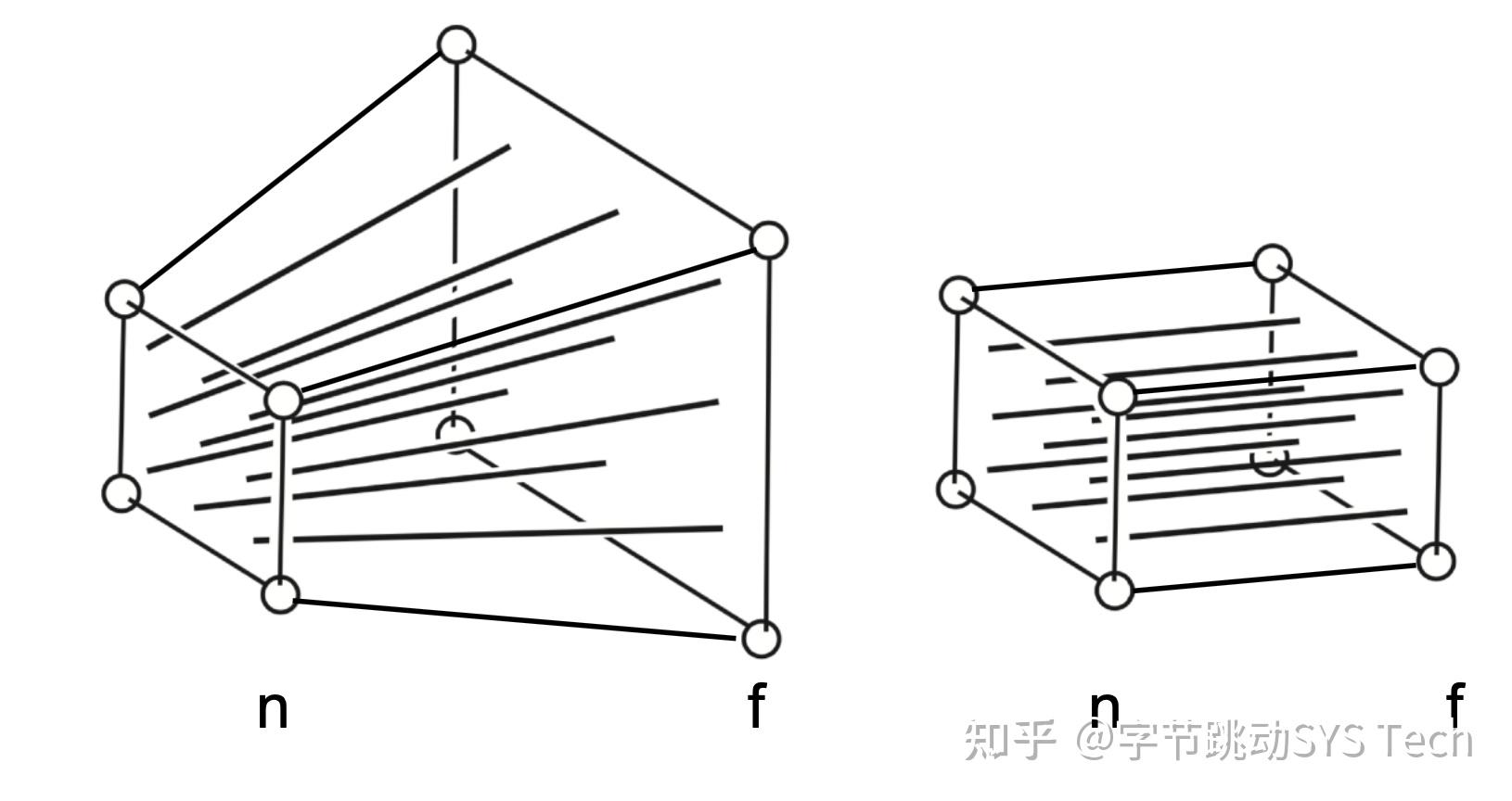
再看下面两个效果图：

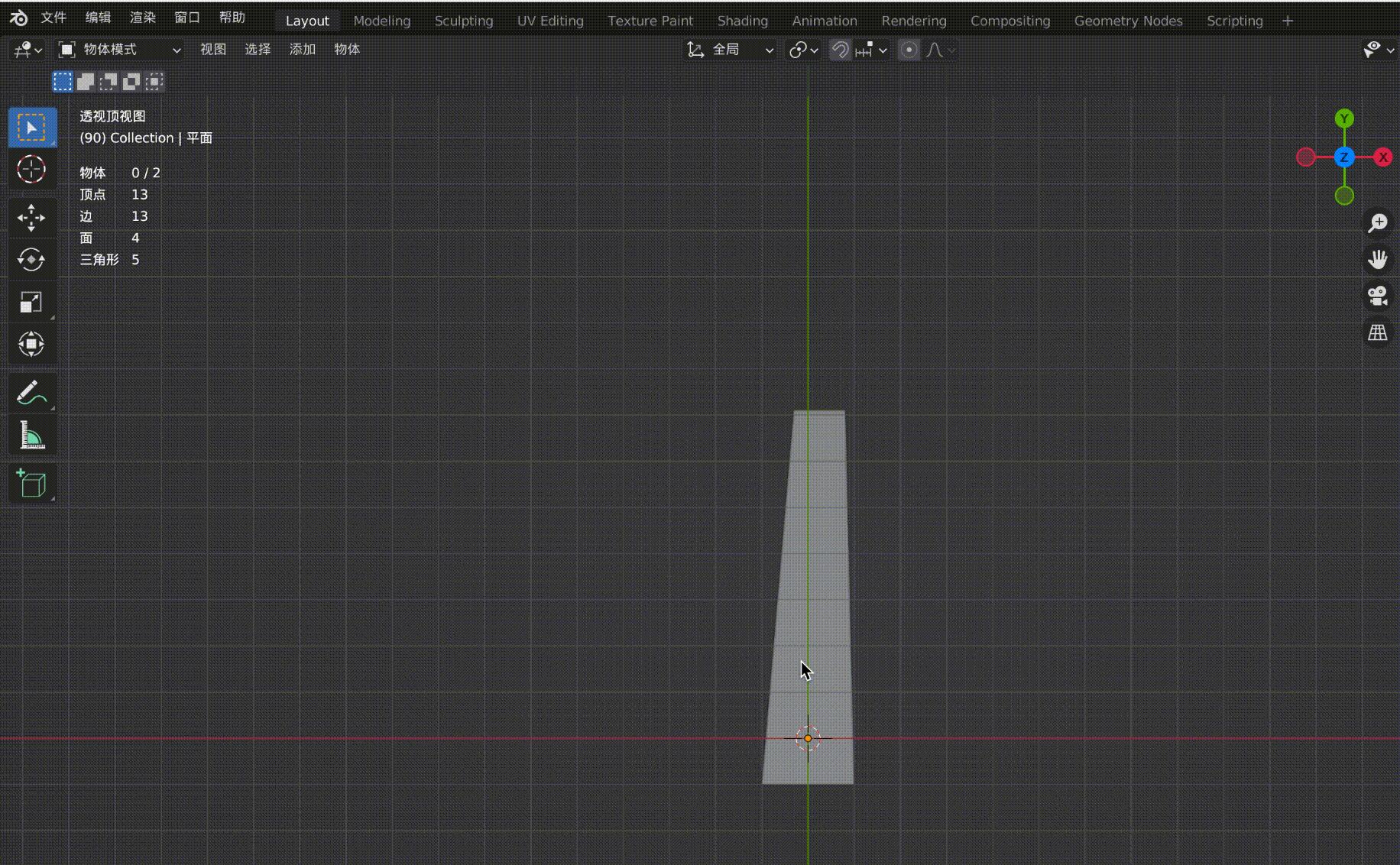
图4-1铁轨是平行的，但在透视投影的作用下，原本的平行线在远处变得相交。图4-2是观察正交视图和透视视图来对比两者区别，同样，在透视投影下，会有近大远小的效果，（图中四个顶点坐标分别为(-1, 10, -20), (1, 10, -20), (-1, -1, 0), (1, -1, 0)，z 轴俯视观察。

关于透视投影部分还有以下几点说明：

这里没有推导透视投影矩阵，而是直接给出了矩阵变换后的效果图，一是希望读者从直观上感受透视投影的效果，二是文章主要内容是光栅化过程的概述，推导不作为重点。如果想了解透视投影的原理，可以学习《GAMES101》或者从《Fundamentals of Computer Graphics》中寻找答案
针对透视投影的效果，最终呈现出来的就是近大远小的视觉效果
无论是正交投影还是透视投影，我们目前做的都是针对几何图形的变换，但是最终的目的是屏幕显示，屏幕显示必然涉及到分辨率和屏幕尺寸。所以，正交投影和透视投影的最后一步都是标准化(图3-2)，最终得到[-1, 1] ^ 3的标准立方体。屏幕上的窗口可以是动态变化的，如：400 x 600，600 x 800等，标准化后通过简单平移 + 缩放即可完成视口变换。

结合我们的模型，对两个三角形做透视投影（图5-1），可以看到两个三角形都在平截头体中，做透视投影后（乘透视矩阵）会先得到标准立方体，然后向[x, y]平面投影（暂时忽略z），得到具有近大远小效果的图（图5-2），图5-2动态比对正交投影和透视投影差别，可以很明显看到透视投影之后，z绝对值大的三角形会变小很多。

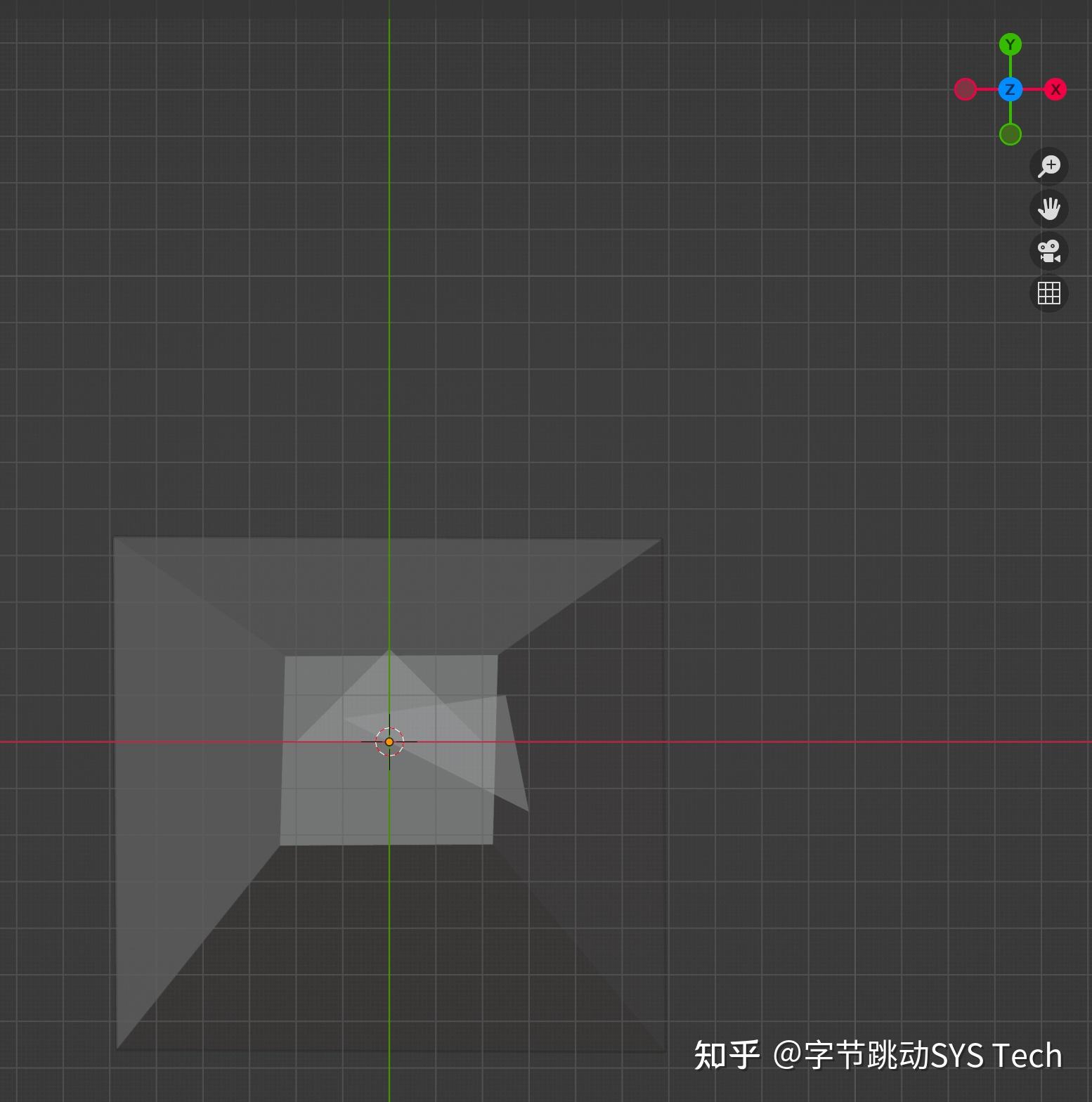
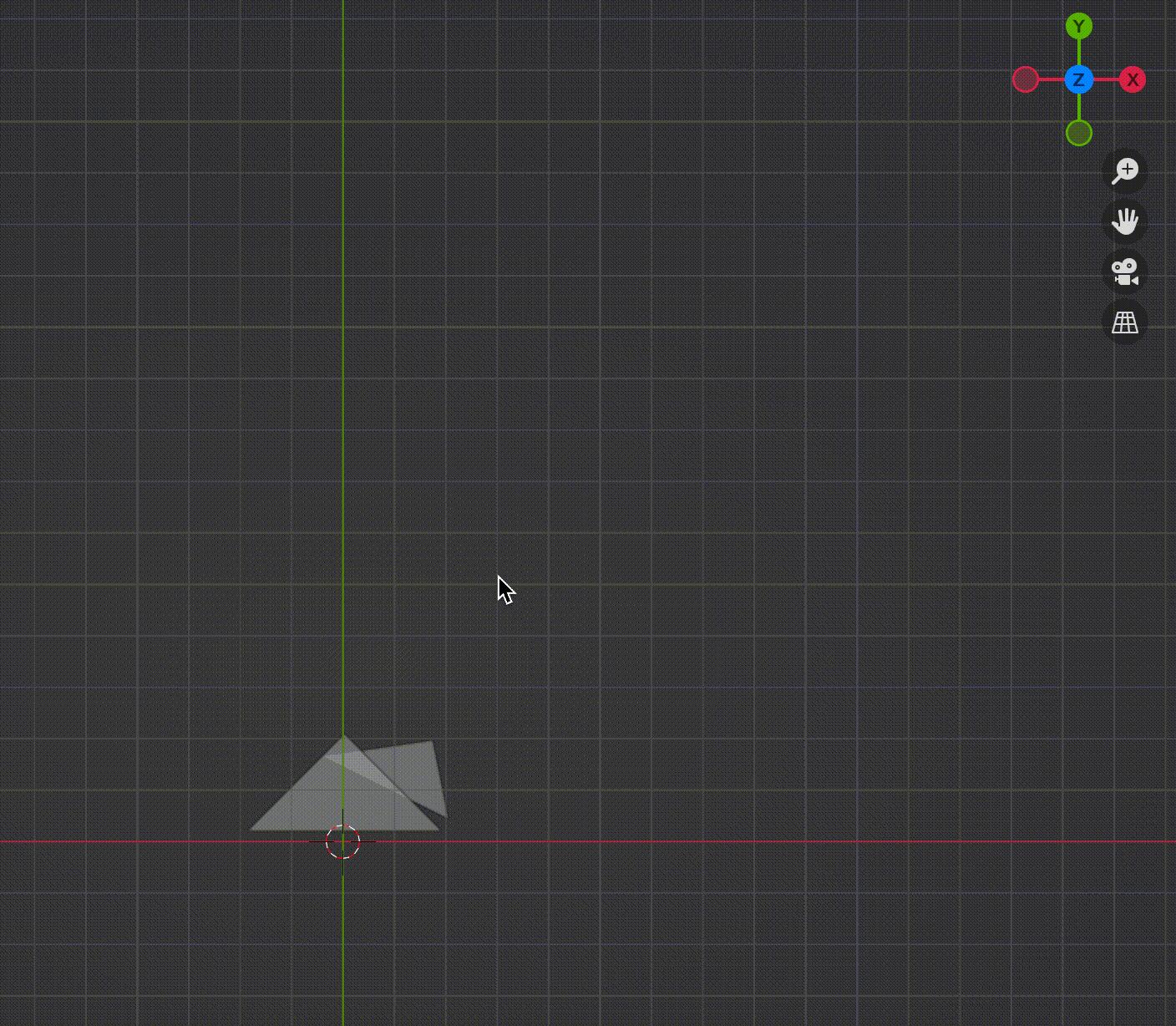
在透视投影之后，得到的是[-1, -1] ^ 3标准立方体，这一小节要讲的是如何将这个标准立方体投影并绘制在屏幕上。具体过程如下图所示。

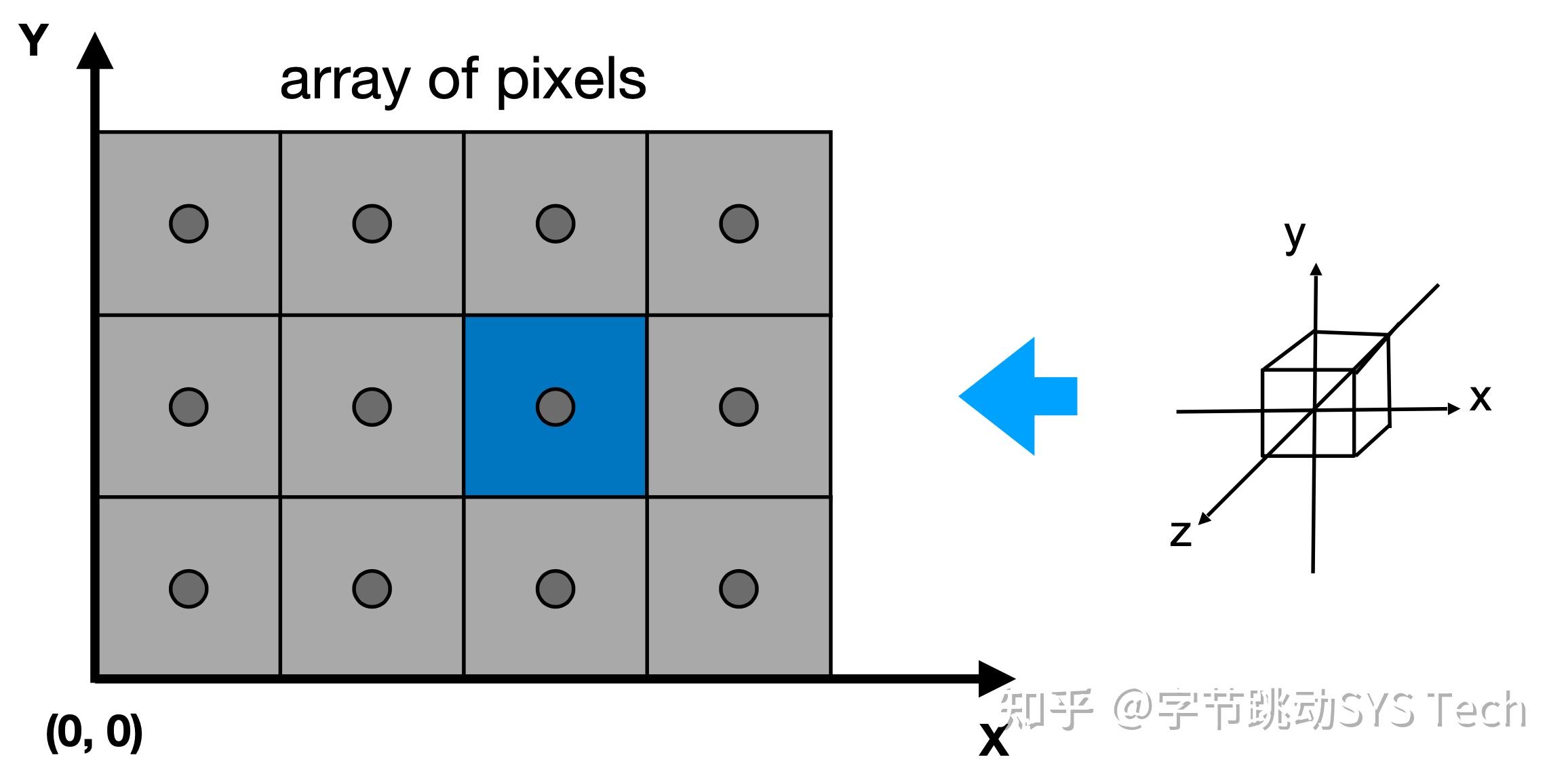
图中有如下两点需要注意：

这里先对屏幕做个简单的抽象，将各个像素抽象为正方形，像素中心即为正方形中心，每个小格子就是一个像素，每个小方格子为 1 * 1，像素位于中心，坐标为(x + 0.5, y+0.5)
上一小节提到了透视投影之后，会标准化成 [-1, 1] ^ 3 的标准化立方体，这时先忽略 z 坐标，根据立方体中各个点的 [x, y] 坐标投在屏幕上。当前的[x, y]是标准化坐标，需要做个简单的平移 + 缩放操作，将 x -> width，y -> height，其中 width、height 代表的屏幕中显示窗口大小，这一步叫做视口变换。

回到我们开始的模型，两个三角形，共有 6 个顶点，这里假设所有的图形都不会被裁剪，我们假设三角形三个顶点在在经历透视投影 --> 标准化 --> 视口变换后的坐标与屏幕坐标关系如下图所示（这里是效果示意图，并不是按照上文模型中的坐标得出）：

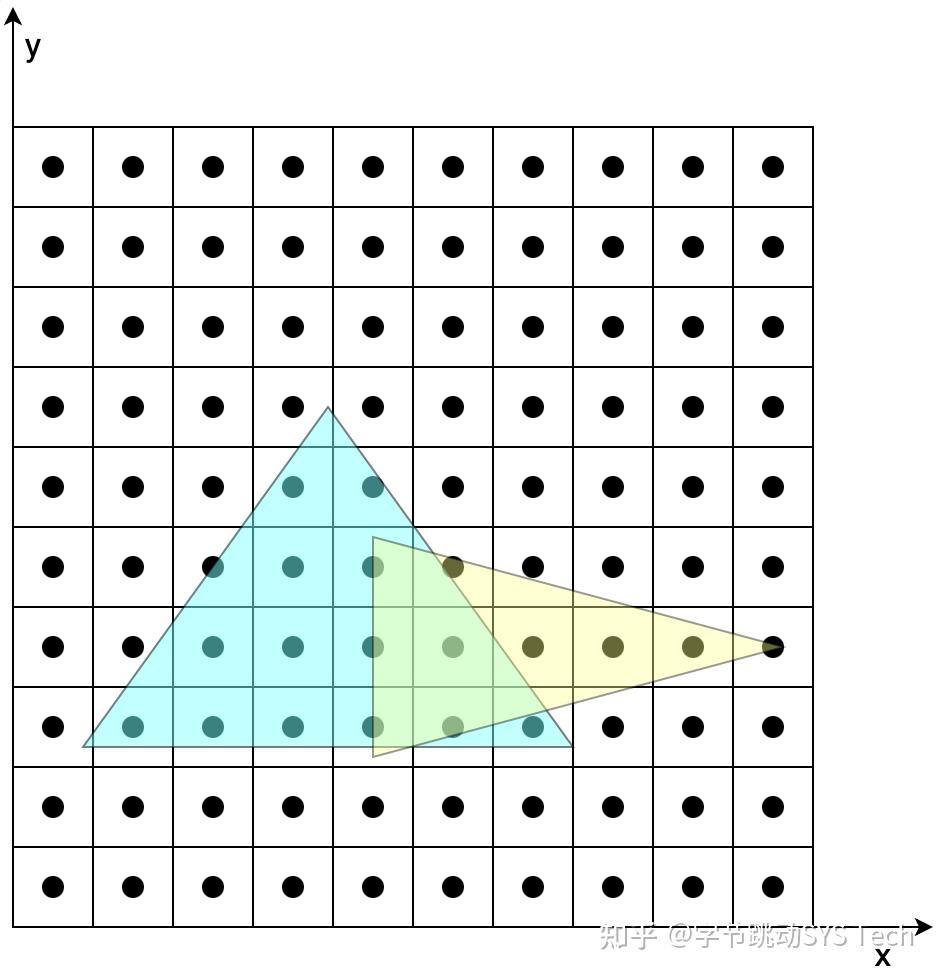
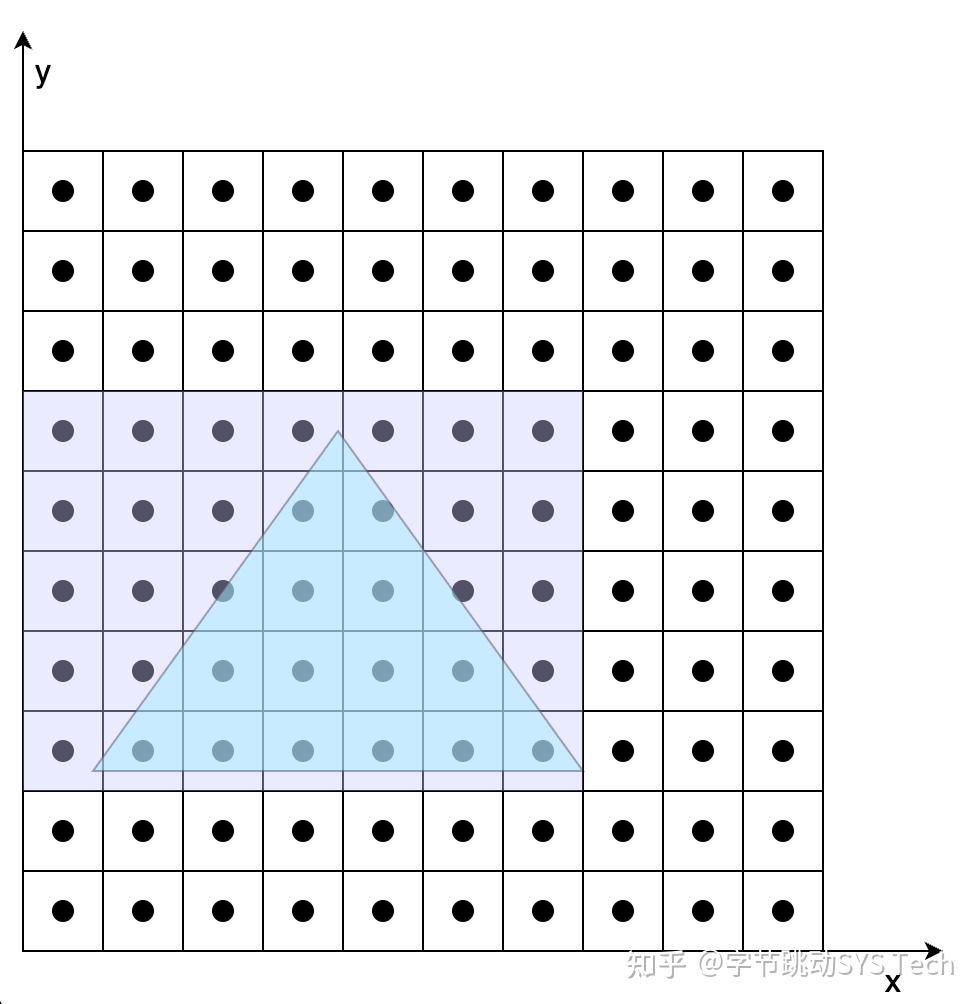
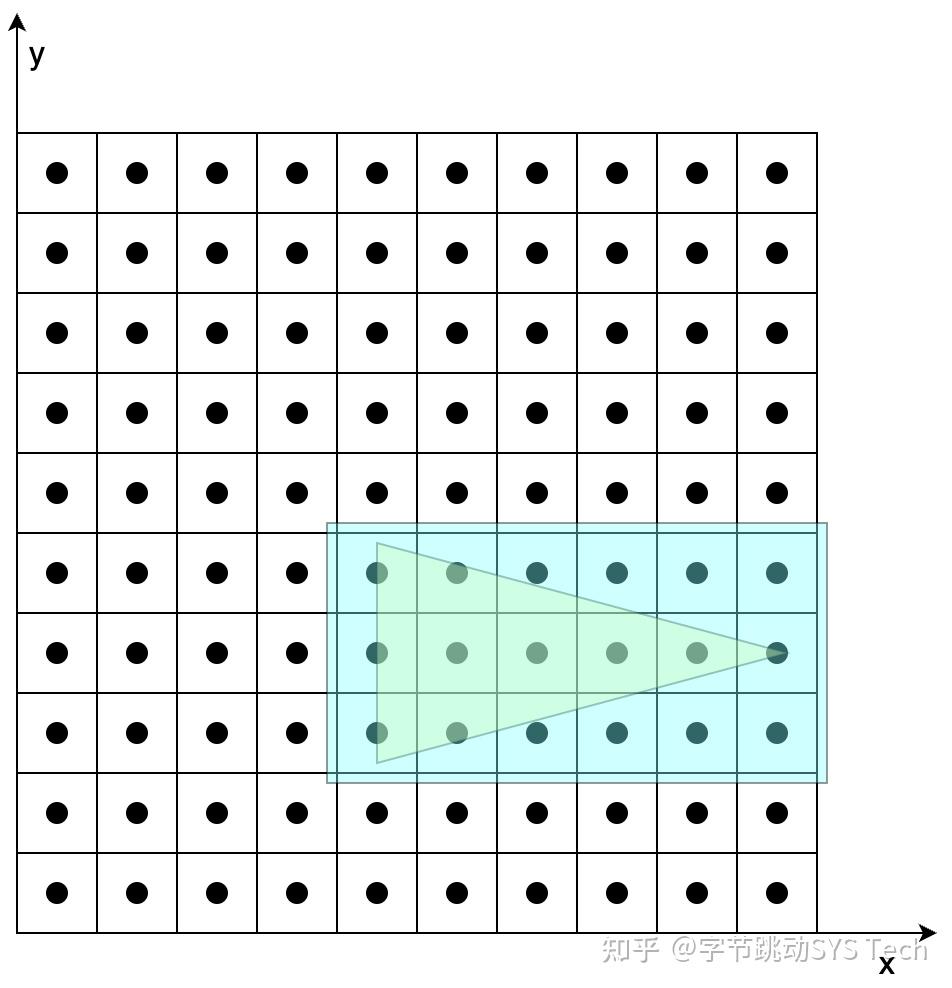
图7-1在不考虑覆盖的情况下，根据两个三角形各自顶点变换后的结果，确定两个三角形的位置。图7-2、7-3是在确定三角形位置后，根据三角形覆盖的像素对其着色。具体步骤如下（以图7-2为例）：

首先根据投影后三个顶点的范围确定一个包围盒，这么做的好处是减少搜索范围
确定了包围盒后，依次判定包围盒中的像素是否在三角形内，这里可以用向量叉乘方法，根据叉乘方向是否同向判定
对于包含在三角形内的像素，对其进行着色。着色过程中，涉及到纹理坐标、法向量等要素的计算，图7-2中我们知道投影之后的三个顶点坐标、纹理坐标、法向量，但是无法获得三角形内任一点的这些数据，这时候就会用到三角形的重心坐标，利用重心坐标通过插值的方法获得三角形内任一点的数据。比如已知三角形三个顶点的纹理坐标(u, v)，想知道三角形内任一点的纹理坐标，就可以通过该点的重心坐标获取，有一点需要切记，这里所说的重心坐标不是投影后的，而是在做透视投影之前的重心坐标，如果要用投影后的重心坐标，需要做修正。对于三角形内法向量计算也是相同道理

不过上面的方法仍然存在两个问题：

图7-2、7-3考虑的都只针对自身三角形的光栅化，对于两个三角形的重叠部分没有考虑，后面讲的深度缓冲会解决这个问题
在判定像素与三角形位置关系时，我们判定的是小方格中心点与三角形关系，即使中心点不在三角形内，像素的小方格子仍然会被三角形覆盖，那么小格子是标记为不亮、还是按照被覆盖的面积来着色，这块如果处理的不好很容易出现锯齿，这里就需要反走样技术，这里不再阐述

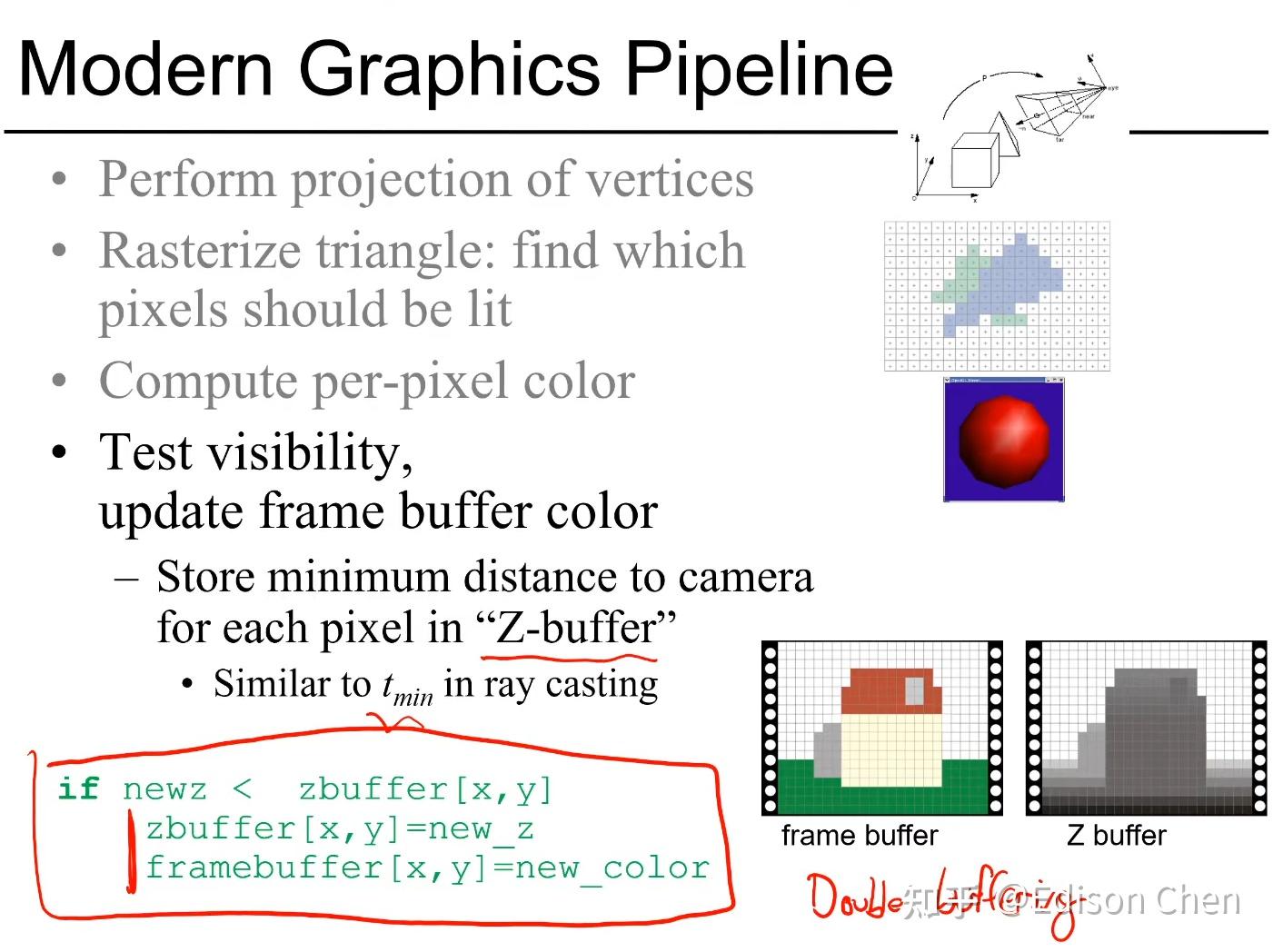
在透视投影之后得到一个标准正方体，在向 x、y 确定平面投影时会遇到这样的情况，对于两个不同顶点，x、y 相同，z 不同，这时候就要借助深度缓冲方法。不考虑透明效果，上述两个顶点，谁距离摄像机近，后面的就会被遮挡。具体方法如下。

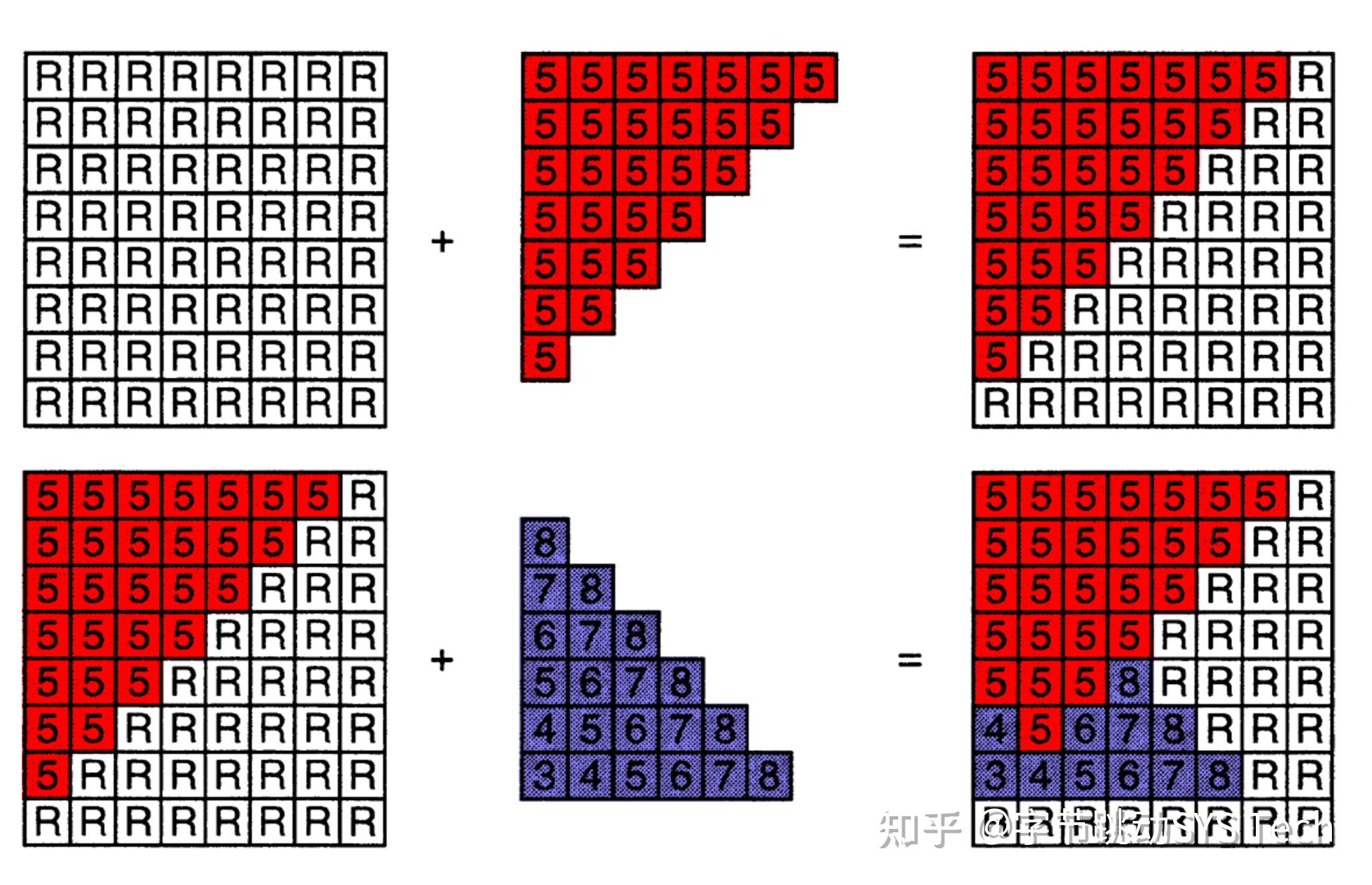
在光栅化过程中，被着色的像素会记录当前点在空间中距离摄像机深度，如果再次被着色的时候，会与之前记录的深度值做比对，如果新的值距离摄像机更近，那么会覆盖掉旧的颜色，否则仍然用旧的颜色。这样就解决了点的覆盖问题，上文仅仅是方法上的阐述，还有很多优化空间，比如我们可以提前深度值的判定，对于被覆盖的点省掉不必要的着色操作。图8-2是实例模型执行深度缓冲后的投影结果。

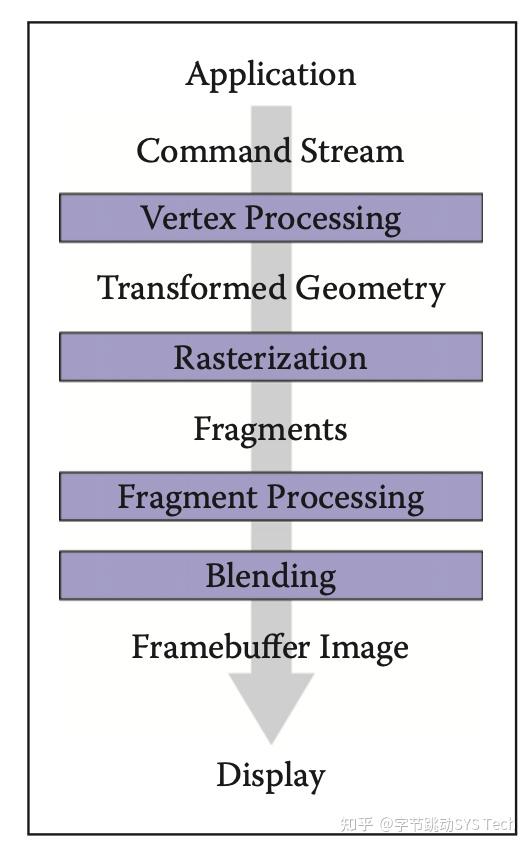
上图是图形管线的主要过程，对照上文例子中的简单模型阐述各个环节工作：

Vertex Processing: 顶点处理，对空间中顶点进行变换，针对我们例子中简化的两个三角形模型，透视投影包含在顶点变换中
Rasterization: 光栅化操作，对于我们这个例子就是对两个三角形做透视投影 --> 然后向[x, y]平面做投影 --> 视口变换，然后判定投影后的三角形内包含了多少像素
Fragment Processing: 像素着色，例子中就是针对投影后两个三角形内的像素进行着色，这里与光照、纹理映射相关，对于三角形任一点的纹理坐标、法向量可以通过三角形顶点的这些信息及三角形重心坐标（透视投影前）计算得到
Blending: 混合上屏，将最终混合结果填充到图形缓冲区，进而刷到屏幕

金三银四的季节，字节跳动STE团队诚邀您的加入！团队长期招聘，北京、上海、深圳、杭州、US、UK 均设岗位，以下为近期的招聘职位信息，有意向者可直接扫描海报二维码投递简历，期待与你早日相遇，在字节共赴星辰大海！若有问题可咨询小助手微信：sys_tech，岗位多多，快来砸简历吧！

光线追踪和光栅化都是很简单的概念。

常见的光线追踪就是从观察者角度发射一条射线到屏幕上像素，之后穿越过这个像素直到击中场景中的物体，击中后就根据物体的属性确定射线是否发生反射、折射或者被吸收掉（这种方式被称为反向光线追踪，其实还有从场景光源发射射线的正向光线追踪、场景物体发射射线等多种光线追踪方式，但是反向光线追踪一般被认为是最适合图形渲染的）。

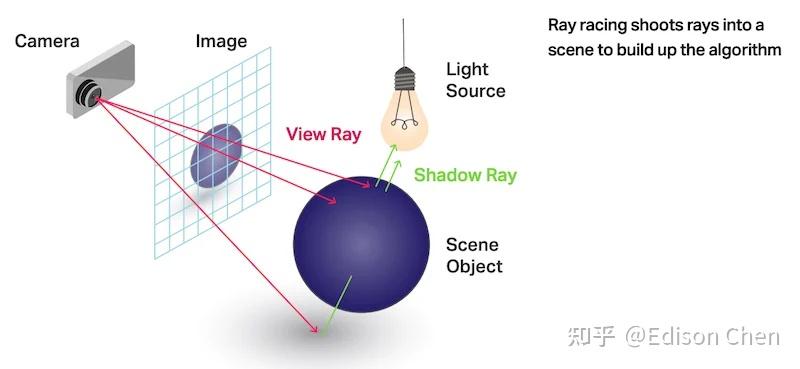
光栅化就是用光栅设置引擎查找出场景中每个三角形在屏幕空间上的位置，然后对这些像素进行计算。

光线追踪的难点在于遍历大量三角形造成计算、带宽需求极大。

这是一个 6 万片的拼图，光线追踪的主要优化方式是尽快从规模 1000 倍于这个拼图的场景中找到被击中的三角形

而光栅化的难点是难以获取屏幕空间之外的物体在画面中的呈现（例如倒影等）。

光线追踪目前的主要优化方式就是使用加速体尽快查找出被击中的三角形，然后配合 DLSS 等空间和时间超采样实现更低的实际渲染负荷。

光栅化也可以实现类似于光线追踪的效果，但是代价是各种兼容性或者性能问题。

以目前的情况看，完全实时光线追踪渲染已经初步实现，而光栅化渲染能做的改进已经不多，所以 GPU 厂商今后主要投放研发资源将会是光线追踪相关的加速技术，而光栅化能做的改进主要是游戏开发商去弄。

光栅在GPU中最主要的就是前端的GeometryProcessorUnit(分配IndexBuffer给每个GPC/SE)。以及每个SM/SE中的VertexAttributeFetchUnit(负责根据前端分来的Indices去Fetch顶点数据)，与Culling Unit/Transform Unit。最后就是最重要的RasterizerUnit与RenderOutputUnit，前者负责处理Transform后的三角形光栅化，后者处理FragmentShader结果的OutputMerge(MSAA/Blend/ZTest)。这几个硬件共同分担图形流水线的工作，既IA->VS->Clip->Viewport->RS->FS->OM的流水线流程。

Primitive Processing : 6 tri(draw) and 12 tri(culling)

Frontend Rasterizer : 192 pix

Backend Rasterizer(ROPs) : 192 pix

Texel Rate : 384 sample

4090:

Primitive Processing : 12 tri(draw) and 24 tri(culling)

Frontend Rasterizer : 192 pix

Backend Rasterizer(ROPs) : 192 pix

Texel Rate : 576 sample

可以看到除了光栅与混合，其他的内容4090都7900XTX的1.5倍到2倍，当然4090是有阉割的，所以并不能达到上面的满血成绩，但也差不了很多就是了，剩下就是频率导致的差异了。

顺便提一句，如今传统光栅已经越来越多限制了，比如4090经常遇到后端强大的浮点单元被前端PD卡住的情况，这样后端的光栅再快也没法超过这个限制浮点就更着一起等了。于是乎计算光栅诞生了，3A在十年前就已经开始尝试ManualVertexFetch，这样压力就全部来到了内存IO上，这也是为什么MeshShader能加速的主要原因之一。再加上如今网格越来越精细导致三角形越来越多也越来越小，传统光栅器与剔除器会有很大限制，各家也都开始用Compute提前做Culling以缓解压力。如7900每周期每ComputeBlock可以给一个Tiangle光栅32个pix，如果三角形小于32个pix就很难让光栅器达到满吞吐，Nv的解决方法是使用TBIMR将tri给Binning在一起让光栅器吞吐量满载(AMD叫BSDR不过从来没启用过)，这也是为什么绿厂优化的游戏喜欢用密集三角形暴力打击按摩店。更软件的解决方案则是Nanite这类GPUDriven，将Primitive抽象成Cluster/Meshlet去保证每像素的三角形占用。

至于3DMark里的测试谁更能反映光栅性能，个人认为MeshShader的那个测试比起WLE或者SW更有说服力，里面有2个对比测试，一个是传统的实现一个是基于计算流程的实现(MeshShader)，没有各种华丽的后期特效等，直接反应硬件的光栅管线的吞吐效率与速度。

是的，你说的是对的!

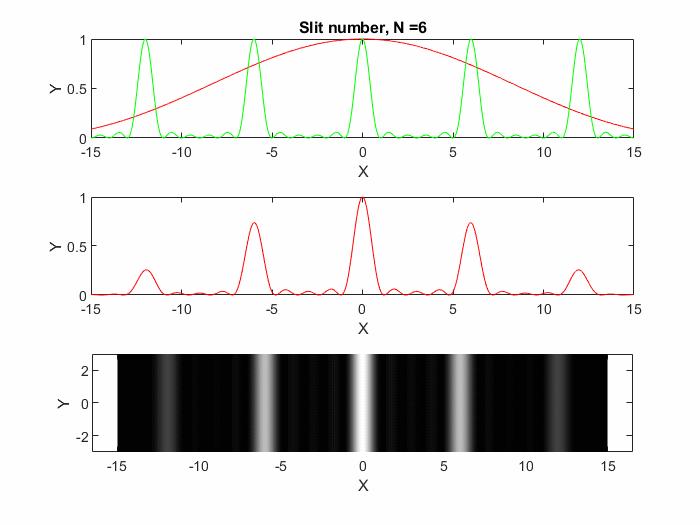
可以参考以下答案，只不过公式中的干涉因子需要更改为多缝干涉因子， $(\frac{sin\frac{N\delta}{2}}{sin\frac{\delta}{2}})^2$ 。理解起来是类似的，就是你说的单缝衍射与多缝干涉的总效果，可以看下图衍射图案随狭缝数量的变化情况。

双缝干涉实验中，缝宽是如何影响条纹形成的？

这里稍微详细展开说一下：

这里默认了解菲涅尔-基尔霍夫衍射公式 $U(P)=-\frac{iA}{2\lambda}\iint_A\frac{\mathrm{exp}[ik(r+s)]}{rs}[cos(\boldsymbol{n},\boldsymbol{r})-cos(\boldsymbol{n},\boldsymbol{s})]d\sigma, \tag{equ. 1}$ 不了解可以参考第七版的《光学原理》^[1]，以上公式的推导可以参考下图，这是书中的原图。

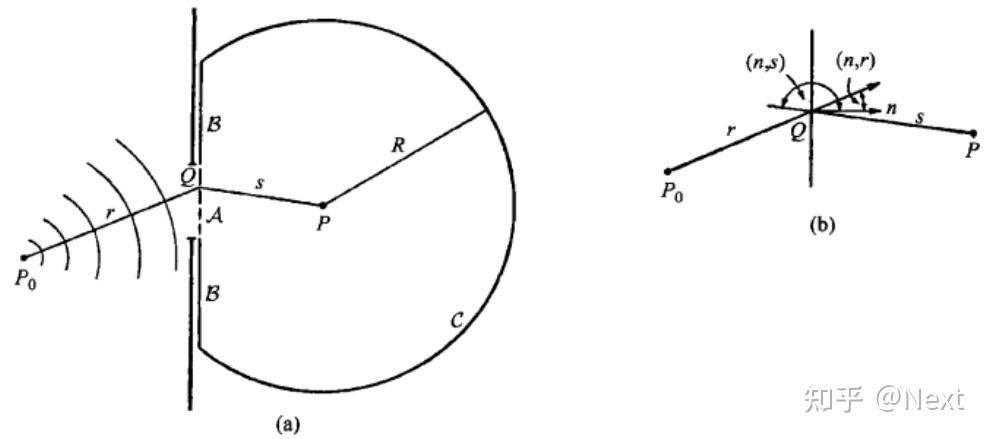
这个公式中的 $[cos(\boldsymbol{n},\boldsymbol{r})-cos(\boldsymbol{n},\boldsymbol{s})]/2$ 在很多教科书中被成为“倾斜因子”， $K(\theta)$ 。对这个公式可以多留意一些，在实际应用中往往考虑孔的大小、光源到孔的距离、孔到观察屏的距离三者之间的相对大小关系做一些近似处理；理解这个对衍射的认识也会更深，可以简化模型做一些实际工程相关的计算；也会发现有些纯“理想”求解很复杂，但是实际问题往往只需要简化的结果（有时则反之）。

有了以上菲涅尔-基尔霍夫衍射公式，便可以计算一些衍射现象，比如矩孔、圆孔、光栅等，在计算之前先说一下两类衍射：菲涅尔衍射与夫琅禾费衍射。

考虑光源到衍射屏以及衍射屏到观察屏的距离 $r,s$ 远大于衍射屏的孔径（参考Fig. 2），那么可以认为：

equ. 1中的 $K(\theta)=[cos(\boldsymbol{n},\boldsymbol{r})-cos(\boldsymbol{n},\boldsymbol{s})]/2\approx1$ （当 $r,s$ 较大时，它们与衍射屏、观察屏法向量基本可认为在一条直线上，注意向量的方向，计算余弦的正负）。
$s\approx z'$

根据以上两点近似，可以将equ. 1简化为 $U(P)=-\frac{i}{\lambda z'}\iint_A\frac{A\mathrm{exp}(ikr)}{r}\mathrm{exp}(iks)d\sigma, \tag{equ. 2}$

令 $U_0=\frac{A\mathrm{exp}(ikr)}{r}$ 为衍射屏孔径后的复振幅，则 $U(P)=-\frac{i}{\lambda z'}\iint_AU_0\mathrm{exp}(iks)d\sigma,$ （这里还是要提醒一下， $\frac{A\mathrm{exp}(iks)}{s}$ 中，分母可以直接使用 $z'$ 代替，但是分子上的却不可以，因为相对来讲， $k=2\pi/\lambda$ 是一个很大的量）。

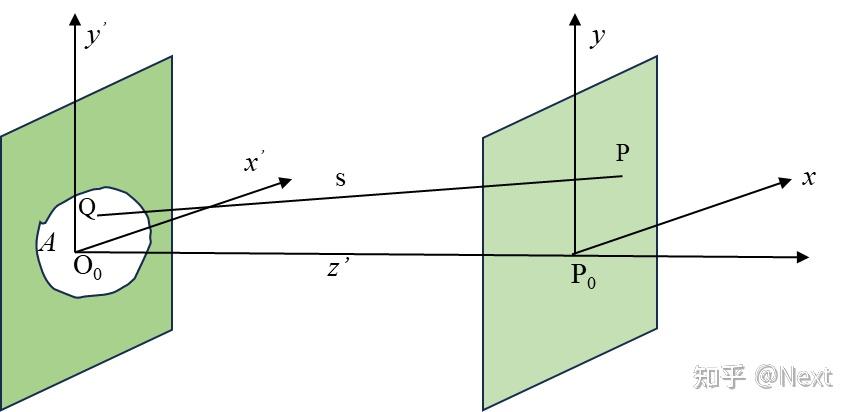
由Fig. 2可知 $s=\sqrt{z'^{2}+\left(x-x'\right)^{2}+\left(y-y'\right)^{2}}$ ，对该式进行幂级数展开，可以得到 $s=z'\Bigg\{1+\frac{1}{2}\Bigg[\frac{(x-x')^2+(y-y')^2}{z'^2}\Bigg]-\frac{1}{8}\Bigg[\frac{(x-x')^2+(y-y')^2}{z'^2}\Bigg]^2+\cdots\Bigg\}, \tag{equ. 3}$ 是菲涅尔衍射还是夫琅禾费衍射衍射的核心就是“研究equ. 3的近似条件”。观察幂级数展开的结果equ. 3, 孔径的大小、观察屏到孔径的距离以及探测图案的大小等都影响了如何对该是进行近似处理。一般认为某些项的存在对 $ks$ 的作用远小于 $\pi$ ^[2] ，那么这些项便可以忽略掉。当 $z'$ 足够大时，导致第三项以后的可以忽略，那么equ. 3近似为 $s=z'+\frac{x^{2}+y^{2}}{2z'}-\frac{xx'+yy'}{z'}+\frac{x'^{2}+y'^{2}}{2z'}, \tag{equ. 4}$ equ. 4就是菲涅尔近似的条件，满足该区域的 $s$ 范围就是菲涅尔衍射区。此时，得到菲涅尔衍射积分公式为 $\boxed {{U}=\frac{\exp\left(\mathrm{i}kz’\right)}{\mathrm{i}\lambda z'}\iint U_0\exp\left\{\frac{\mathrm{i}k}{2z'}\Big[(x-x')^{2}+(y-y')^{2}\Big]\right\}\mathrm{d}x'\mathrm{d}y'} \tag{equ. 5}$ 当观察屏距离更远的地方，随着传播距离的不断扩大，衍射的“光线”也会越散，即观察衍射图案的尺度也越大，这时孔径的大小相对于传播距离已经小到可以忽略了。这时，equ. 4可以进一步近似（这一步的处理是针对公式equ. 5，可以理解夫琅禾费衍射是菲涅尔衍射的一种，实际实验中很难在这个距离下实验，一般使用透镜），近似掉最后一项，变成 $s\approx z'+\frac{x^2+y^2}{2z'}-\frac{xx'+yy'}{z'}, \tag{equ. 6}$ equ. 5就是夫琅禾费衍射的近似条件。进而，得到夫琅禾费衍射积分公式为 $\boxed{U(P)=\frac{\exp\left(\mathrm{i}kz'\right)}{\mathrm{i}\lambda z'}\mathrm{exp}\left[\frac{\mathrm{i}k}{2z'}(x^{2}+y^{2})\right]\iint U_0\exp\left[-\mathrm{i}k\left(\frac{x}{ z'}x'+\frac{y}{z'}y'\right)\right]\mathrm{d}x'\mathrm{d}y'}\tag{equ. 7}$ 利用夫琅禾费衍射积分公式看一下单缝衍射情况，单缝夫琅禾费衍射的光路图可以如Fig. 4搭建。（实验上实际找到满足夫琅禾费衍射衍射条件是很难的，往往借助一个透镜，在透镜焦面观察衍射图案与实际无透镜在观察屏看见的衍射图案基本是一致的，只不过图案大小会有一定的比例缩放，这部分可以参考光学教材^[2]）。

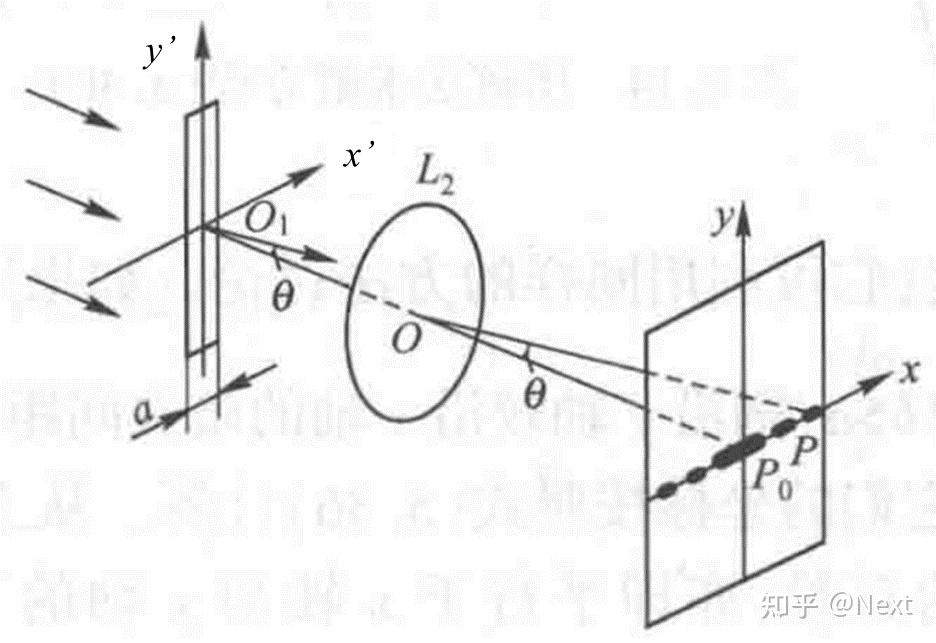
为了简单，只看一条切线上的光强分布，令 $y=0$ ，针对夫琅禾费衍射积分公式，将 $z'$ 替换为透镜的焦距 $f$ 。这里默认平面波均匀照射到狭缝，透光处的复振幅均匀且为1，即 $U_0=1$ 。至此，可以得到单缝夫琅禾费衍射积分公式为 $U(P)=\frac{\exp\left(\mathrm{i}kf\right)}{\mathrm{i}\lambda f}\mathrm{exp}\left[\frac{\mathrm{i}kx^{2}}{2f}\right]\int_{\frac{-a}{2}}^{\frac{a}{2}} \exp\left[-\mathrm{i}k\left(\frac{x}{ f}x'\right)\right]\mathrm{d}x',\tag{equ. 8}$ 对该公式积分，得到单缝衍射 $P$ 处的复振幅分布为 $U(P)=a\frac{\exp\left(\mathrm{i}kf\right)}{\mathrm{i}\lambda f}\exp\biggl[ik\biggl(\frac{x^2}{2f}\biggr)\biggr]\frac{\sin\frac{kxa/f}2}{\frac{kxa/f}2},\tag{equ. 9}$ 令 $x=0$ ,得到 $P_0$ 处的复振幅 $U(P_0)=a\frac{\exp\left(\mathrm{i}kf\right)}{\mathrm{i}\lambda f}$ ，光强 $I(P)=U(P)[U(P)]^*$ ，可以将 $P$ 点的光强写为 $\boxed{ I(P)=I_0\biggl(\frac{\sin\frac{kxa/f}2}{\frac{kxa/f}2}\biggr)^2}\tag{equ. 10}$ 其中， $I0=U(P_0)^2$ 为 $P_0$ 处的光强，以上是单缝衍射 $x$ 方向光强分布的结果。

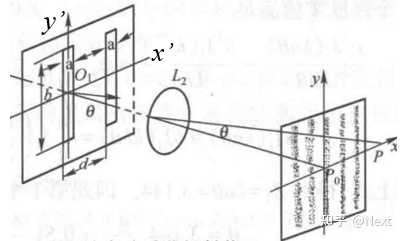
多缝衍射的复振幅可以就看做不同缝衍射复振幅的叠加，以双缝为例， $P$ 点的复振幅可以表示为 $U(P)=\frac{\exp\left(\mathrm{i}kf\right)}{\mathrm{i}\lambda f}\mathrm{exp}\left[\frac{\mathrm{i}k}{2f}(x^{2})\right]\int_{\frac{-a}{2}}^{\frac{a}{2}} \exp\left[-\mathrm{i}k\left(\frac{x}{ f}x'\right)\right]\mathrm{d}x'\int_{d+\frac{-a}{2}}^{d+\frac{a}{2}} \exp\left[-\mathrm{i}k\left(\frac{x}{ f}x'\right)\right]\mathrm{d}x',\tag{equ. 11}$ 求解equ. 11得到 $\begin{align} U(P)&=a\frac{\exp\left(\mathrm{i}kf\right)}{\mathrm{i}\lambda f}\exp\biggl[ik\biggl(\frac{x^2}{2f}\biggr)\biggr]\biggl(\frac{\sin\frac{kxa/f}2}{\frac{kxa/f}2}+\frac{\sin\frac{kxa/f}2}{\frac{kxa/f}2}\mathrm{exp}(-\mathrm{i}kxd/f)\biggr) \\&=a\frac{\exp\left(\mathrm{i}kf\right)}{\mathrm{i}\lambda f}\exp\biggl[ik\biggl(\frac{x^2}{2f}\biggr)\biggr]\frac{\sin\frac{kxa/f}2}{\frac{kxa/f}2}(1+\mathrm{exp}(ikxd/f))\tag{equ. 12}, \end{align}$ $I(P)=U(P)[U(P)]^*$ ，可以得到双缝衍射 $P$ 点的光强（equ. 12 $\Rightarrow$ equ. 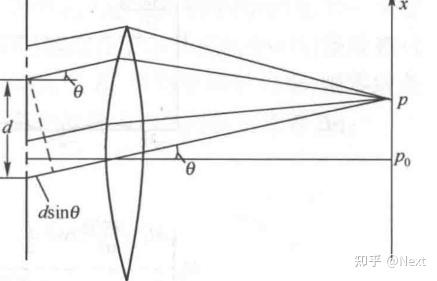13用了欧拉公式和二倍角公式）为 $\boxed{I(P)=4I_0\biggl(\frac{sin\frac{kxa/f}{2}}{\frac{kxa/f}{2}}\biggr)^2cos^2(kxd/2f)}\tag{equ. 13}$

其中双缝之间的位相差 $kxd/f\approx\frac{2\pi}{\lambda}dsin\theta$ ，一般教科书都将其定义为 $\delta$ ，这个对于理解光栅方程非常重要！

得到双缝衍射光强的分布后，可以了解其复振幅为两个单缝复振幅的叠加，那么多缝也是同样的原理，这样便可以得到多缝衍射 $P$ 处的复振幅为 $\begin{align} U(P)&=\sum_{k=1}^N U_0\frac{sin\frac{kxa/f}{2}}{\frac{kxa/f}{2}}\mathrm{exp}[i(k-1)\delta]\\ &= U_0\frac{sin\frac{kxa/f}{2}}{\frac{kxa/f}{2}}\frac{1-\mathrm{exp}(iN\delta)}{1-\mathrm{exp}(i\delta)} \tag{equ.14}\\&=U_0\frac{sin\frac{kxa/f}{2}}{\frac{kxa/f}{2}}\frac{sin\frac{N\delta}{2}}{sin\frac{\delta}{2}}\mathrm{exp}[i(N-1)\delta/2] ,\end{align}$

(equ. 14的获得可以利用级数展开 $\sum_{k=0}^{n} x^k=\frac{x^{n+1}-1}{x-1}，$ 之后“凑成”以上样子即可)。利用 $I(P)=U(P)*U(P)^*$ 得到 $\boxed{I(P)=I_0\biggl(\frac{sin\frac{kxa/f}{2}}{\frac{kxa/f}{2}}\biggr)^2\biggl(\frac{sin\frac{N\delta}{2}}{sin\frac{\delta}{2}}\biggr)^2}\tag{15}$ 以上得到的equ. 15便是多缝衍射光强分布，有了它就可以理解光栅的衍射。理解光栅的衍射主要是分析相邻单元在不同角度入射下带来的相位差（注意反射、透射光栅相位差的计算），这样很更容易理解光栅方程。光栅也可以看成多缝的衍射（但实际的光栅计算只需要计算一个单元加上周期性边界条件），现在再来看一下本文开始的Fig. 1；Fig. 1（为了看着方便，图中的强度做了归一化处理）中最上端图中红色表征单缝“衍射因子”，红线为多缝的“干涉因子，”中间图的红色曲线为多缝衍射的实际光强分布。看这幅图还是可以看出不少规律的，比如谱线位置或者衍射方向与狭缝数量、单缝衍射因子无关，随着狭缝数量的增多，谱线越加细而亮，这些可以理解光栅的分辨本领^[3]，这里就不多啰嗦了。

如果把光谱信息比作世间万物自带的密码，光栅就是人类用于“解码”的“芯片”。日前，中国科学院长春光机所成功研发了制造这种高端“解码芯片”的母机，打破我国在该领域受制于人的局面，并达到国际领先水平。

11月11日，国家重大科研装备研制项目“大型高精度衍射光栅刻划系统的研制”在中科院长春光机所通过验收。验收专家组表示，该项成果填补了国内空白，也将扭转我国光谱仪器行业“有器无心”的状况。

项目负责人唐玉国研究员介绍，光栅是一种具有纳米精度周期性微结构的精密光学元件，除了在各类光谱仪中担当“芯片”角色外，还在天文学、激光器、光通讯、信息存储、新能源等诸多领域中具有重要应用。虽然在生活中很难直接看到光栅的身影，但它遍及农轻重、海陆空、吃穿用等各行各业，实实在在影响着人们的生活。

唐玉国告诉记者，光栅面积大，可获得高集光率和分辨本领；精度高，可获得更好的信噪比。但是，同时将光栅“做大”和“做精”属于世界性难题。随着科技不断发展，大面积高精度中阶梯光栅已经成为制约我国相关领域技术发展的短板，尽快研制此类光栅也是各光栅强国之间竞争的焦点。

来源:新华网

大型高精度衍射光栅刻划系统

400mm×500mm中阶梯光栅

对于三角形内的任意一点P

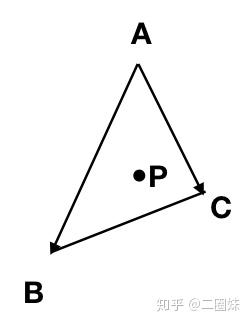
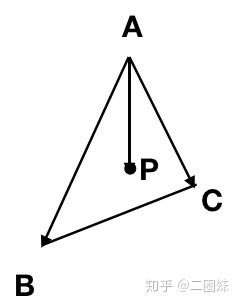
其实学过向量的就能想到, $\overrightarrow{AP}、\overrightarrow{AB}、\overrightarrow{AC}$ 线性相关。

可以写成:

$\overrightarrow{AP} =u\overrightarrow{AB} + v\overrightarrow{AC} \\$

这个式子我们可以拆开：

$A - P = u(A - B) + v(A - C)\\$

得到：

$P = (1 - u - v)A + uB + vC\\$

这也是P的表示，其中 $0 \le u, v \le 1$ . 来取特殊一点的 u，v 可以得到 A, B, C.

这个式子长的很像 AB 上任意一点D的计算：

$D = A + t(B - A), 0 \le t \le 1\\$

也就是线性插值

$D = (1 - t)A + tB, 0 \le t \le 1 \\$

当然也可以把ABC看成坐标系，始于A点，基为： $\overrightarrow{AB}$ 和 $\overrightarrow{AC}$ 。所以这个叫做重心坐标系（barycentric，bary- 重的）也能得到式子：

$\overrightarrow{AP} =u\overrightarrow{AB} + v\overrightarrow{AC}\\$

继续写：

$u\overrightarrow{AB} + v\overrightarrow{AC} + \overrightarrow{PA} = 0\\$

考虑二维三角形，拆一拆：

$u\overrightarrow{AB}_x + v\overrightarrow{AC}_x + \overrightarrow{PA}_x = 0\\$

$u\overrightarrow{AB}_y + v\overrightarrow{AC}_y + \overrightarrow{PA}_y = 0 \\$

甚至我们还可以把它写成矩阵形式：

$\begin{bmatrix} u & v & 1 \end{bmatrix} \begin{bmatrix} \overrightarrow{AB}_x \\ \overrightarrow{AC}_x \\ \overrightarrow{PA}_x \end{bmatrix} = 0 \\$

$\begin{bmatrix} u & v & 1 \end{bmatrix} \begin{bmatrix} \overrightarrow{AB}_y \\ \overrightarrow{AC}_y \\ \overrightarrow{PA}_y \end{bmatrix} = 0 \\$

实际上我们都可以看做是我们在寻找向量 (u, v, 1) 同时垂直于向量 $(\overrightarrow{AB}_x, \overrightarrow{AC}_x,\overrightarrow{PA}_x)$ 和向量 $(\overrightarrow{AB}_y, \overrightarrow{AC}_y,\overrightarrow{PA}_y)$ 。这不就是叉乘么？

同时这给了我们一个有了P点，求 u 和 v 的思路。

xvector = (B_x - A_x, C_x - A_x, A_x - P_x) yvector = (B_y - A_y, C_y - A_y, A_y - P_y) u = xvector x yvector # 因为我们讨论的是二维的三角形，如果 u 的 z 分量不等于1则说明P点不在三角形内

然后我们来代码阶段，因为我们的计算中涉及到浮点数，可能u的z分量不会一定等于1.0,

令 u 的三个分量是 (a, b, c),我们代入原式子：

$a\overrightarrow{AB} + b\overrightarrow{AC} + c\overrightarrow{PA} = 0\\$

$P = (1 - a/c - b/c)A + a/cB + b/cC, c \ne 0\\$

看C++代码：

Vec3f barycentric(Vec2f A, Vec2f B, Vec2f C, Vec2f P) { Vec3f s[2]; for (int i=2; i--; ) { s[i][0] = C[i]-A[i]; s[i][1] = B[i]-A[i]; s[i][2] = A[i]-P[i]; } Vec3f u = cross(s[0], s[1]); if (std::abs(u[2])>1e-2) // dont forget that u[2] is integer. If it is zero then triangle ABC is degenerate  return Vec3f(1.f-(u.x+u.y)/u.z, u.y/u.z, u.x/u.z); return Vec3f(-1,1,1); // in this case generate negative coordinates, it will be thrown away by the rasterizator }

整个Python的：

def barycentric(A, B, C, P): """  A, B, C, P: Vector3, points  return u: Vector3, barycentric coordinate of P  """ s1 = Vector3(B.x - A.x, C.x - A.x, A.x - P.x) s2 = Vector3(B.y - A.y, C.y - A.y, A.y - P.y) u = s1.cross(s2) if abs(u.z) > EPSILON: # means this works, we have the P inside triangle return Vector3(1-(u.x+u.y)/u.z, u.x/u.z, u.y/u.z) return Vector3(-1,1,1)

重心坐标在CG中的应用可以有以下：

填充三角形

之前我也想过这个问题，因为我们生成图像，归根结底是在于画像素点，那么如果我们要填充一个三角形，对于一个一个的像素点，我们只需要放到上述函数里面去，就可以判断P是否在三角形内，如果在三角形内，我们就去画它。这样填一个三角形的算法可以就是O(image.width * image.height),我们甚至可以进一步降低复杂度，对于一个三角形来说，我们可以由它的bounding box, 只需要检测它的bounding box里面的点，然后就可以用来填充。

z-buffer

其实这里也不止于 z-buffer,我们已经把P点表示成了A，B，C的线性组合形式，那么对于P点的z，我们也可以这样来看，我们把P点z值也可以看成A，B，C的线性组合，其实不仅仅是P点的z，对于P点的任意性质，只要是我们觉得可以用线性组合来看的，我们都可以用这个坐标系统。

任何矩阵都可以分解为旋转、缩放、旋转三个相乘的矩阵（查阅线性代数）：

$M = R_1scale(\delta_1,\delta_2,\delta_3)R_2\\$

它的逆很容易求出（旋转矩阵为正交阵，它的逆就是它的转置）:

$M = R_2^Tscale(1/\delta_1,1/\delta_2,1/\delta_3)R_1^T\\$

用几何的方式来看，我们平移变换就是把它移动 $(T_x, T_y, T_z)$ ，那么逆就是把它反向移，也就是 $(-T_x, -T_y, -T_z)$ :

$T = \begin{pmatrix} 1 & 0 & 0 & T_x \\ 0 & 1 & 0 & T_y\\ 0 & 0 & 1 & T_z\\ 0 & 0 & 0 & 1 \end{pmatrix} \\$

逆:

$T^{-1} = \begin{pmatrix} 1 & 0 & 0 & -T_x \\ 0 & 1 & 0 & -T_y\\ 0 & 0 & 1 & -T_z\\ 0 & 0 & 0 & 1 \end{pmatrix} \\$

同样用几何的方式来看，缩放放大 $(S_x, S_y, S_z)$ ,所以我们缩小回去，也就是 $(1/S_x, 1/S_y, 1/S_z)$ :

$S = \begin{pmatrix} S_x & 0 & 0 & 0 \\ 0 & S_y & 0 & 0 \\ 0 & 0 & S_z & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \\$

逆:

$S^{-1} = \begin{pmatrix} 1/S_x & 0 & 0 & 0 \\ 0 & 1/S_y & 0 & 0 \\ 0 & 0 & 1/S_z & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \\$

旋转矩阵有特殊的性质，它是一个正交矩阵，它的逆刚好是它的转置：

$R = \begin{pmatrix} A & B & C & 0 \\ D & E & F & 0\\ G & H & I & 0\\ 0 & 0 & 0 & 1 \end{pmatrix} \\$

逆就是它的转置：

$R^{-1} = \begin{pmatrix} A & D & G & 0 \\ B & E & H & 0\\ C & F & I & 0\\ 0 & 0 & 0 & 1 \end{pmatrix} \\$

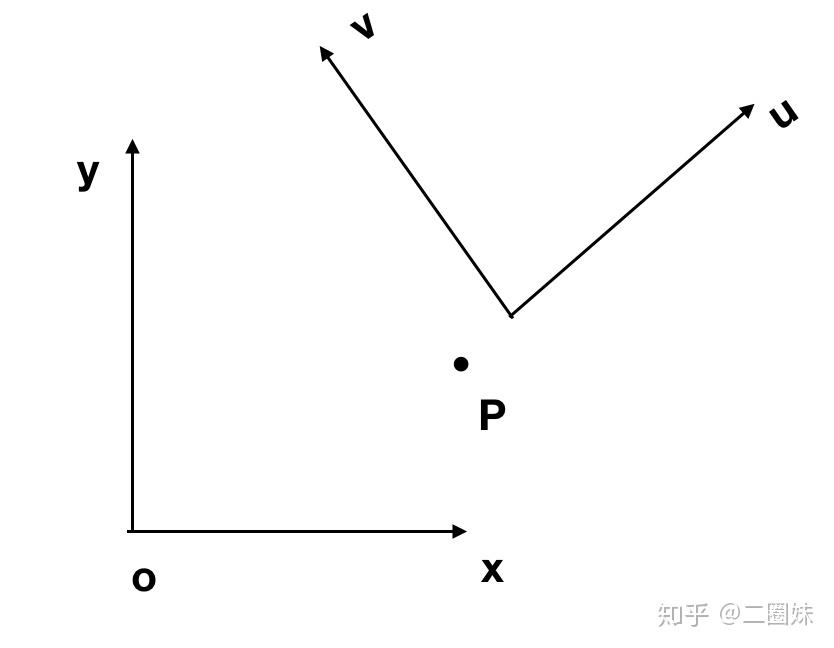
坐标变换的意思是，比如我们看一个点P，它在xy系统中的表示是 $(x_P, y_P)$ ,它在uv系统中的坐标是 $(u_p, v_p)$ , uv 在xy坐标系中是 $(x_u,y_u),(x_v,y_v)$ ，因为在它本身坐标系中是(1,0)和(0,1).

$\begin{pmatrix} x_p \\ y_p \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & x_e\\ 0 & 1 & y_e \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x_u & x_v & 0\\ y_u & u_v & 0\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} u_p \\ v_p \\ 1 \end{pmatrix} \\$

逆变换：

$\begin{pmatrix} u_p \\ v_p \\ 1 \end{pmatrix} = \begin{pmatrix} x_u & y_u & 0\\ x_v & y_v & 0\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & -x_e\\ 0 & 1 & -y_e \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x_p \\ y_p \\ 1 \end{pmatrix} \\$

三维坐标系也是一样，同时这也给出了我们坐标变换的公式：

$\begin{pmatrix} x_p \\ y_p \\ z_p \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 & x_e\\ 0 & 1 & 0 & y_e \\ 0 & 0 & 1 & z_e \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x_u & x_v & x_w & 0 \\ y_u & y_v & y_w & 0 \\ z_u & z_v & z_w & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} u_p \\ v_p \\ w_p \\ 1 \end{pmatrix} \\$

逆变换：

$\begin{pmatrix} u_p \\ v_p \\ w_p \\ 1 \end{pmatrix} = \begin{pmatrix} x_u & y_u & z_u & 0 \\ x_v & y_v & z_v & 0 \\ x_w & y_w & z_w & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & -x_e\\ 0 & 1 & 0 & -y_e \\ 0 & 0 & 1 & -z_e \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x_p \\ y_p \\ z_p \\ 1 \end{pmatrix} \\$

这就是坐标变换，让我们可以把一个点从一个坐标系变到另一个坐标系。

变换矩阵经常需要把 [a,A] x [b, B] 矩形范围变换到 [c, C] x [d, D]。我们可以采取以下的操作：

平移(a,b)移动到原点
缩放矩形，达到目标矩形的大小
原点移动到 (c,d)

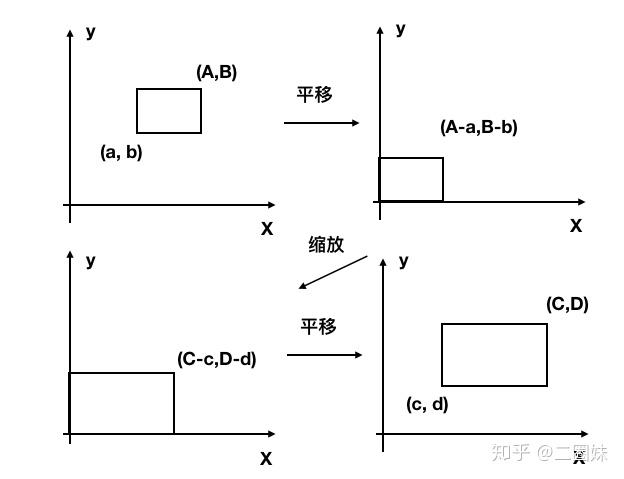
$\begin{align} window &= translate(c,d) scale(\frac{C-c}{A-a}, \frac{D-d}{B-b}) translate(-a,-b) \\ &= \begin{pmatrix} 1 & 0 & c\\ 0 & 1 & d\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} \frac{C-c}{A-a} & 0 & 0\\ 0 & \frac{D-d}{B-b} & 0\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & -a\\ 0 & 1 & -b\\ 0 & 0 & 1 \end{pmatrix} \\ &= \begin{pmatrix} \frac{C-c}{A-a} & 0 & \frac{cA-Ca}{A-a}\\ 0 & \frac{D-d}{B-b} & \frac{dB-Db}{B-b}\\ 0 & 0 & 1 \end{pmatrix} \end{align} \\$

思考方式是通用的，然后这种思考方式感觉去做别的变换也都是可以‘拿来主义’。

OpenGL本身没有摄像机(Camera)的概念，但我们可以通过把场景中的所有物体往相反方向移动的方式来模拟出摄像机，产生一种我们在移动的感觉，而不是场景在移动。

lookat矩阵是由这些东西来定义的：摄像头位置，它看向的方向，以及向上的up方向。由于“OpenGL中我们知道摄像机指向z轴负方向”，所以给图如下：

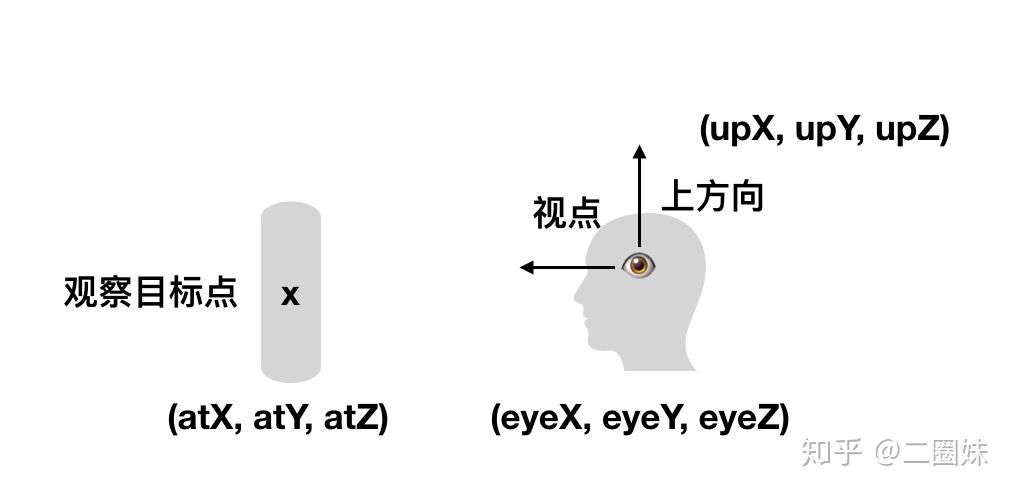
那么我们知道实际上坐标系的方向是这样的，我们用(eye - center)就能得到z轴的方向，然后我们定义一个向上的方向 $up(0, 1, 0)$ ,我们可以用 $up \times z$ - 向上的方向叉乘z得到x方向，再用 $z \times x$ - z方向叉乘x得到y.

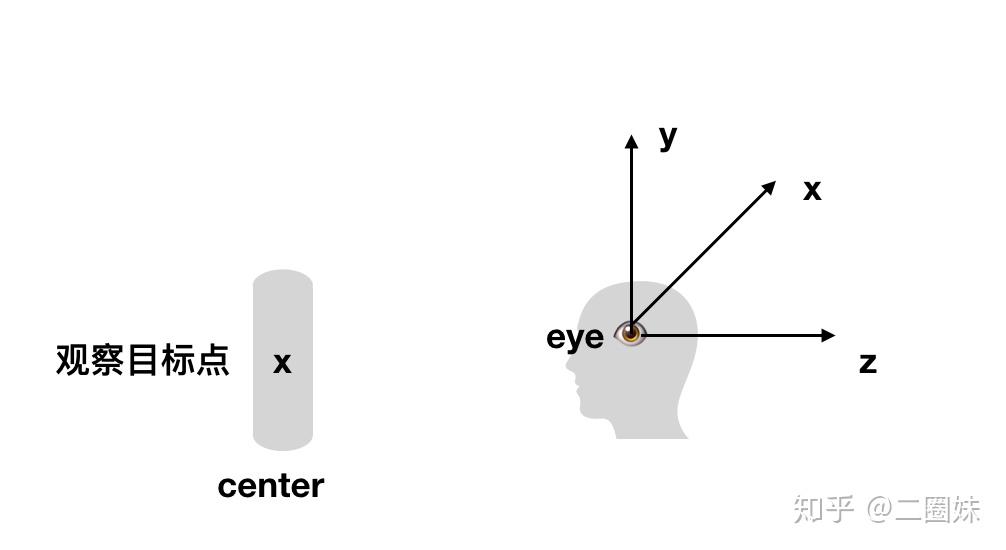
也可以参考这个图：

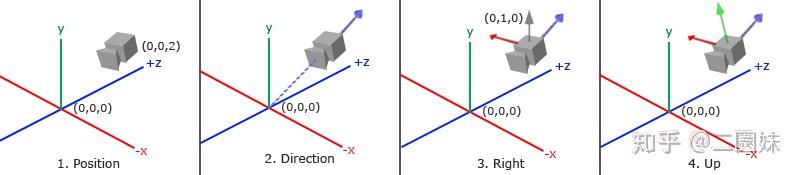
再根据之前的坐标变换知识，于是我们可以得到lookat矩阵：

$lookat = \begin{pmatrix} R_x & R_y & R_z & 0 \\ U_x & U_y & U_z & 0 \\ D_x & D_y & D_z & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & -P_x\\ 0 & 1 & 0 & -P_y \\ 0 & 0 & 1 & -P_z \\ 0 & 0 & 0 & 1 \end{pmatrix} \\$

R - 右向量，也就是相机坐标系x在世界坐标系中的表示
U - 上向量，也就是相机坐标系y在世界坐标系中的表示
D - 方向向量，也就是相机坐标系z在世界坐标系中的表示
P - 相机在世界坐标系中位置

我感觉也可以这样理解，Rotation、Translation其实是相机在世界坐标系中的变换：

$M_{camera} = M_{Translation} * M_{Rotation}\\$

其实我们用它来看物体也就是它这个变换的逆变换：

$M_{camera}^{-1}= M_{Rotation}^{-1} * M_{Translation}^{-1} \\$

而相机的旋转矩阵的逆是它的转置，平移矩阵的逆也可以在就是把它移回去，这样也跟上面的lookat矩阵一样。写个代码：

void lookat(Vec3f eye, Vec3f center, Vec3f up) { Vec3f z = (eye-center).normalize(); Vec3f x = cross(up,z).normalize(); Vec3f y = cross(z,x).normalize(); Matrix Minv = Matrix::identity(); Matrix Tr = Matrix::identity(); for (int i=0; i<3; i++) { Minv[0][i] = x[i]; Minv[1][i] = y[i]; Minv[2][i] = z[i]; Tr[i][3] = -center[i]; } ModelView = Minv*Tr; }

我们再来求另一个常见矩阵，我们现在有模型都在[-1,1]*[-1,1]*[-1,1]正方体中，我们想把它映射到位置[x,x+w]*[y,y+h]*[0,d]中，我们的操作是：

平移：先把[-1,1]*[-1,1]*[-1,1]平移到[0,2]*[0,2]*[0,2]
缩放：[0,2]*[0,2]*[0,2]缩放到[0,1]*[0,1]*[0,1]
缩放：[0,1]*[0,1]*[0,1]缩放到[0,w]*[0,h]*[0,d]
平移：[0,w]*[0,h]*[0,d]移动到[x,x+w]*[y,y+h]*[0,d]

就跟窗口变换十分类似，我们可以来求得这个变换的矩阵：

$\begin{pmatrix} 1 & 0 & 0 & x\\ 0 & 1 & 0 & y \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} w & 0 & 0 & 0\\ 0 & h & 0 & 0 \\ 0 & 0 & d & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1/2 & 0 & 0 & 0\\ 0 & 1/2 & 0 & 0 \\ 0 & 0 & 1/2 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 1\\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 1 \end{pmatrix} \\$

计算得：

$\begin{pmatrix} w/2 & 0 & 0 & x + w/2\\ 0 & h/2 & 0 & y + h/2 \\ 0 & 0 & d/2 & d/2 \\ 0 & 0 & 0 & 1 \end{pmatrix}\\$

这个矩阵是OpenGL中的Viewport矩阵。

投影有两种：

正交：

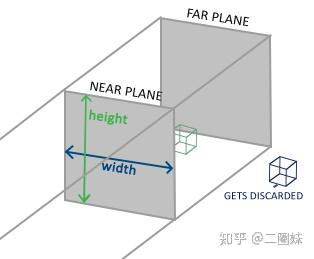
透视：

我们都知道透视法则-近大远小，就像上图，平行的铁路公路在我们的眼睛里也是会在远处相交的。

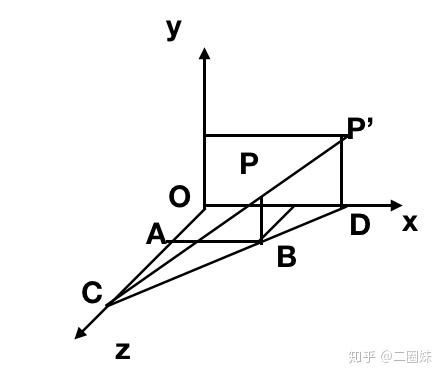
如果我们要将P点投影到 z=0 平面上的 P' 点，camera放在C点(0, 0, c)，很容易可以按照比例算出 |AB|/|AC| = |OD|/|OC| 可知： x/(c-z) = x'/c，可知：

$x' = \frac{x}{1-z/c} \\$

$y' = \frac{y}{1-z/c}\\$

所以我们也可以得到投影矩阵:

$\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & -1/c & 1 \end{pmatrix}\\$

参考:

摄像机
坐标系统
glViewport
Perspective projection

我们现在先复习一下，我们经过了画点、画线，填三角形之后已经能画出来一些东西了，现在我们有好几条路可以走，那就是

光（上帝说“要有光”）
纹理（不然就填白色和随机颜色么？）
数学（之前做的所有事情就是简单的把x,y对应的画到图像上来）

这里我们做的事就是简单的给我们的模型一点‘方向光’，注意我这里说了一专有名词‘方向光’，所以还会有别光（暂且不表）。方向光就是类似太阳光一样的，我们只考虑它的方向：

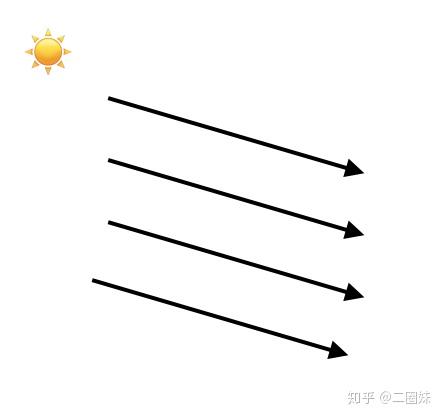
对于一束光，我们到达物体表面的能量实际上是：

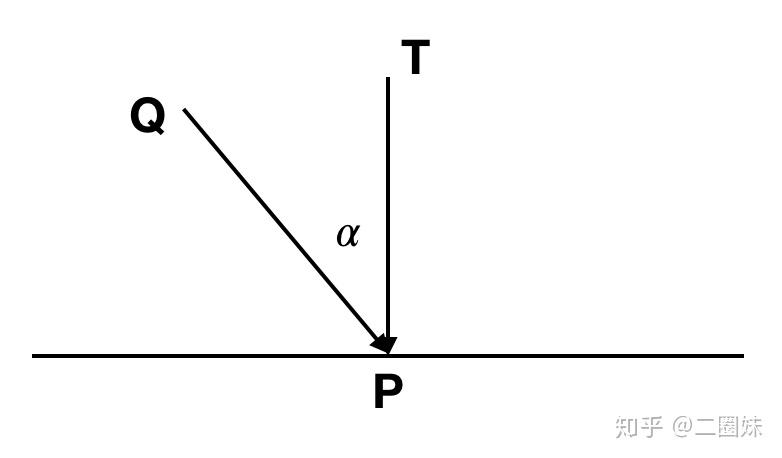
它的强度 Icosα， α是物体光与物体的法向量的夹角。

如果我们用 $\overrightarrow{L}$ 表示光的方向， $\overrightarrow{N}$ 指向物体光照处'向内的'法向量，那么

$cos\alpha = \frac{\overrightarrow{L} \cdot \overrightarrow{N}}{|\overrightarrow{L}| \cdot |\overrightarrow{N}|} \\$

这里我们就必须要考虑一些数学问题了，物体我们放在这，然后有光的方向:

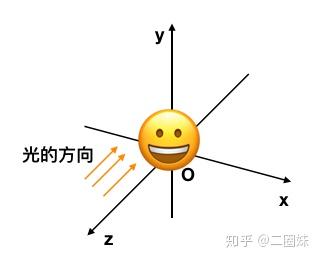
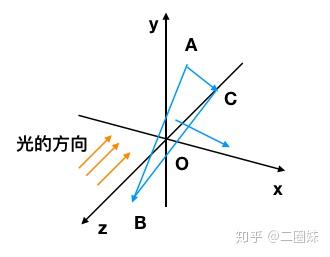
那么'朝内的'法向量可以这样得到 $\overrightarrow{AC} \times \overrightarrow{AB}$ ，然后正交化：

这里我们先做很多简化操作：

光的方向是 Vec3f light(0, 0, -1), 强度就是1
假设每个三角形收到光照的强度相同，都是 Icosα
三角形法向量 $\overrightarrow{AC} \times \overrightarrow{AB}$
当然我们还要知道 cosα 大于0才有意义，我们不可能减去光o(╯□╰)o

核心代码：

Vec3f norm = cross(world_coords[2] - world_coords[0], world_coords[1] - world_coords[0]); norm.normalize(); float intensity = light*norm; if (intensity > 0) { triangle(screen_coords, image, TGAColor(intensity*255,intensity*255,intensity*255,255)); }

看效果：

妈妈他是凸嘴。我们换一个光的方向。

更吓人了。。。。他嘴巴怎么长后面了。。

simplelight

compile & run：

$ g++ -std=c++11 main.cpp tgaimage.cpp model.cpp -o main $ https://www.zhihu.com/topic/main

造成这个问题的原因很简单，我们就是一股脑的把三角形画出来了，没有考虑三角形的先后顺序，正如画画一样，我们应该先画远处的东西，如果近处有什么东西把它给覆盖了，我们就不会看到远处的东西，这里我们就是画三角形的时候没有考虑先后顺序。那么这个问题要怎么解决呢？

这里我们先继续回顾一下三角形重心坐标：

$P = (1 - a/c - b/c)A + a/cB + b/cC, c \ne 0\\$

这里其实有一个很cool的点，就是我们把P表示成三角形三个顶点的线性组合，再回忆一下线性插值，其实对于P点的任何性质，我们都可以利用类似线性插值，把它变成三个顶点的组合：

$P_z = (1 - a/c - b/c)A_z + a/cB_z + b/cC_z, c \ne 0 \\$

所以这里就给了我们提示，对于任意一点P，我们算出它的z值，如果z值更靠近我们，那么我们就用它来替换已经画上的点，否则我们则不更新P点。

同样我们也只用考虑画布上的所有的点的P值，可以用一个二维的数组来表示，不过我们这里偷懒，就用一维的数组，因为画布上的(x,y)点可以写成(x + y *width)，可以这样来转换:

int idx = x + y*width; int x = idx % width; int y = idx / width;

同时注意我们在把物体坐标系做映射时，需要保留z值，所以一些计算我们最好就用float.同时我们也需要注意在转换坐标系的时候我们需要注意还是需要把 x 和 y 变成int，否则有些地方会因为浮点数的原因for loop不会覆盖所有的像素，会有黑色部分产生：

Vec3f world2screen(Vec3f v) { // 注意这里我们还是保留了int这个操作，因为我们的画像素的for loop要用到这个x和y  // 如果都是浮点数，那么for loop有些可能无法顺利进行  // 我们再加上0.5来四舍五入  return Vec3f(int((v.x+1.)*width/2.+.5), int((v.y+1.)*height/2.+.5), v.z); }

第二个需要注意的点是我们物体的位置和朝向，这里我们把z-buffer初始化为负无穷大，然后如果P.z更大意味更靠近我们。

void triangle(Vec3f *pts, float *zbuffer, TGAImage &image, TGAColor color) { Vec2f bboxmin(std::numeric_limits<float>::max(),std::numeric_limits<float>::max()); Vec2f bboxmax(std::numeric_limits<float>::min(),std::numeric_limits<float>::min()); Vec2f clamp(image.get_width()-1, image.get_height()-1); for (int i = 0; i < 3; i++) { for (int j = 0; j < 2; j++) { bboxmin[j] = std::max(0.f, std::min(bboxmin[j], pts[i][j])); bboxmax[j] = std::min(clamp[j], std::max(bboxmax[j], pts[i][j])); } } Vec3f P; for (P.x = bboxmin.x; P.x <= bboxmax.x; P.x++) { for (P.y = bboxmin.y; P.y <= bboxmax.y; P.y++) { Vec3f bc_screen = barycentric(pts[0], pts[1], pts[2], P); if (bc_screen.x < 0 || bc_screen.y < 0 || bc_screen.z < 0 ) continue; P.z = 0; for (int i=0; i<3; i++) P.z += pts[i][2]*bc_screen[i]; if (zbuffer[int(P.x+P.y*width)] < P.z) { image.set(P.x, P.y, color); zbuffer[int(P.x+P.y*width)] = P.z; } } } }

看结果:

KrisYu/tinyrender

直线与三角形相交，首先三角形是在平面上，直线与平面的交点比较容易求得。

平面公式：

$\overrightarrow{N} \cdot P + D = 0 \\$

直线可以写成：

$Q = A + t(B - A), 0 \le t \le 1\\$

代入：

$\overrightarrow{N} \cdot (A + t(B - A)) + D = 0 \\$

$t = \frac{-D - \overrightarrow{N} \cdot A}{ \overrightarrow{N} \cdot (B - A)}\\$

当我们计算出来 t 之后，再代回原公式得到交点P：

$P = A + t(B - A)\\$

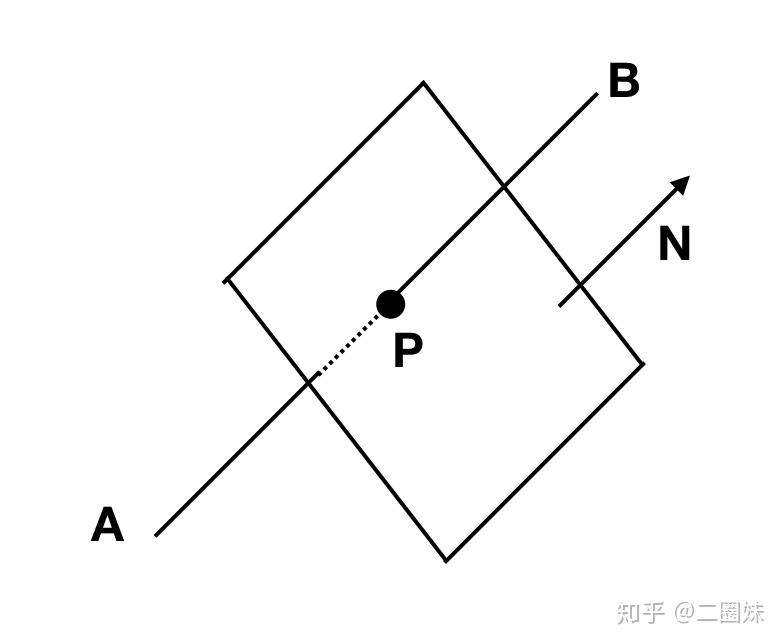
这里有一点点危险的地方 $\overrightarrow{N} \cdot (B - A)$ 可能为0，这个时候就意味着 N 和 AB 垂直，那么直线与平面平行，它与平面没有交点。

当直线与平面相交之后，我们需要判断交点是否在三角形内，之前在二维平面上，我们用过这样的办法：判断 $P_0P$ 和三角形边 $P_0P_1$ 的法向量的 n 的点乘是否小于0来看P点是否位于三角形边的‘左侧’。

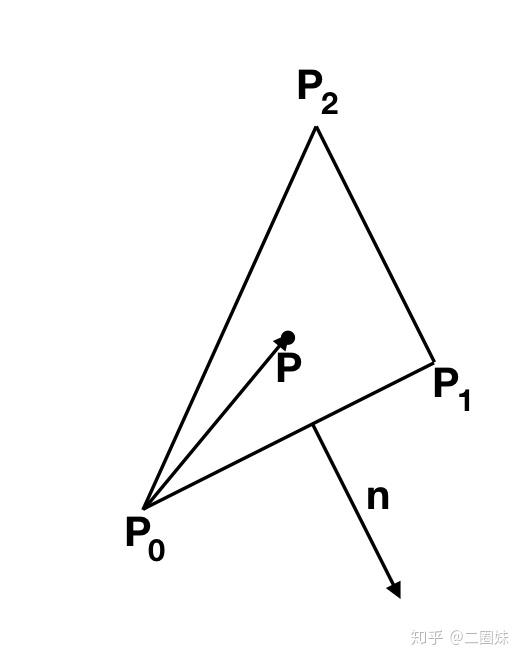
实际上这个思路也可以推广到三维：

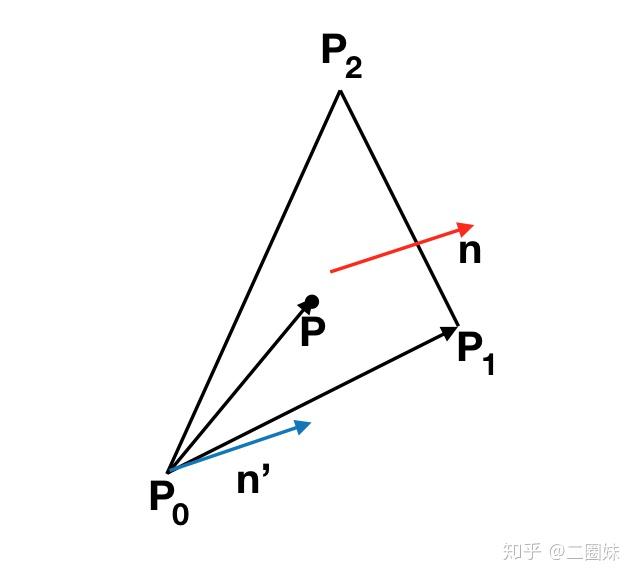
n 是三角形的normal，也是平面的normal是 $P_0P_1 \times P_0P_2$ 结果。如果P点在三角形内侧，那么 $P_0P_1 \times P_0P$ 的向量 n' 会方向相同，也就是它们的点乘会大于0.

查看另外两边，也会有类似的效果，所以三角形和射线相交可以这样写：

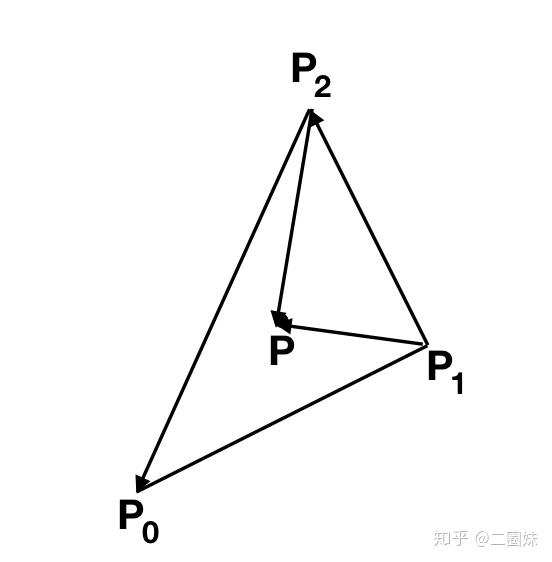
bool ray_triangle_intersect(const Vec3f A, const Vec3f B, const Vec3f p0, const Vec3f p1, const Vec3f p2){ // 1. find the p point  Vec3f n = cross(p1 - p0, p2 - p0); float d = -n*p1; Vec3f AB = B - A; if (fabsf(n*AB) < epsilon) return false; float t = (-d - n*A )/(n * AB); // t < 0 means opposite direction of AB  if (t < 0 ) return false; Vec3f p = A + AB*t; if (cross(p1-p0, p-p0) * n < 0 ) return false; if (cross(p2-p1, p-p1) * n < 0 ) return false; if (cross(p0-p2,p-p2) * n < 0 ) return false; return true; }

当然我们交点P也是直接求出来了。

重心坐标系我之前也写过 → 三角形重心坐标

$P = wA + uB + vC \\ 0 \le w, u, v \le 1 \\ w + u + v = 1$

实际上重心坐标系也叫面积坐标，如果三角形面积为1的话，那么P点分割的三角形有以下性质：

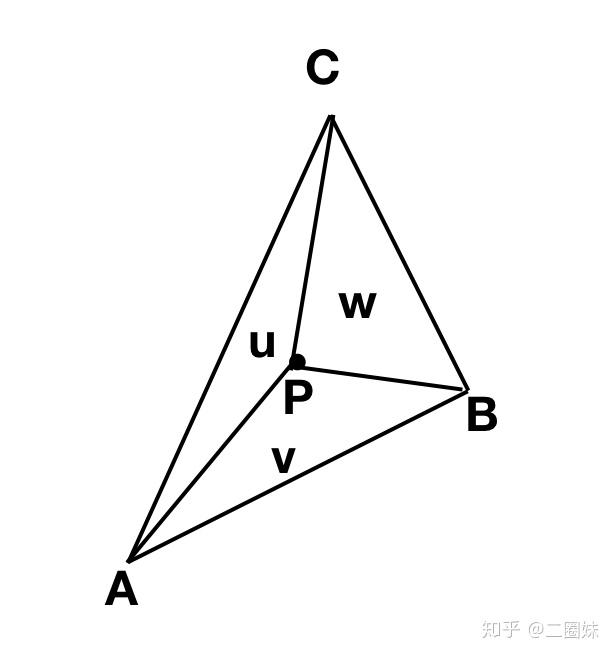
如果想验证也很简单：

$S_{ABC} = |AB \times AC| \\ S_{ABP} = |AB \times AP| = |AB \times (uAB + v AC)| = v |AB \times AC|\\$

所以这给我们提供了一个比较简单的重心坐标系的算法，再结合算法一,我们可以很容易的算出 u, v.

// AB: ray, p0p1p2: triangle bool bary_centric_coordinate(const Vec3f A, const Vec3f B, const Vec3f p0, const Vec3f p1, const Vec3f p2, float &u, float &v){ // 1. find the p point, same as above  Vec3f n = cross(p1 - p0, p2 - p0); float area = n.norm(); float d = -n*p1; Vec3f AB = B - A; if (fabsf(n*AB) < epsilon) return false; float t = (-d - n*A )/(n * AB); if (t < 0 ) return false; Vec3f p = A + AB*t; // 2. find u,v  Vec3f uvector, vvector; if (cross(p2-p1, p-p1) * n < 0 ) return false; if ((vvector = cross(p1-p0,p-p0)) * n < 0) return false; if ((uvector = cross(p0-p2,p-p2)) * n < 0) return false; u = uvector.norm()/area; v = vvector.norm()/area; return true; }

实际上代码跟算法一很多部分都是一致的，只是这里我们加了计算 u, v 而已。

Möller-Trumbore算法我感觉和重心坐标系差不多，只是加入了更多线性代数的优化？三角形依旧是 ABC，假设光线源点为O，方向为D，有相交点满足：

$O + tD = A + u(B-A) + v(C-A) \\ O - A = -tD + u(B-A) + v(C-A)$

矩阵形式：

$\begin{bmatrix} -D & (B-A) & (C-A) \end{bmatrix}\begin{bmatrix} t \\ u \\ v \end{bmatrix} = O - A \\$

利用Cramer's rule，可知：

$\begin{bmatrix} t \\ u \\ v \end{bmatrix} = \frac{1}{\begin{bmatrix}|-D & E_1 & E_2|\end{bmatrix}}\begin{bmatrix} |T & E_1 & E_2| \\ |-D & T & E_2| \\ |-D & E_1 & T| \end{bmatrix} \\$

其中 T = O - A, E1 = B - A, E2 = C - A.

又线性代数中行列式的性质：

$|ABC| = -(A \times C) \cdot B = -(C \times B) \cdot A\\$

继续：

$\begin{bmatrix} t \\ u \\ v \end{bmatrix} = \frac{1}{(D \times E_2) \cdot E_1}\begin{bmatrix} (T \times E_1) \cdot E_2 \\ (D \times E_2) \cdot T \\ (T \times E_1) \cdot D \end{bmatrix} = \frac{1}{ P \cdot E_1}\begin{bmatrix} Q \cdot E_2 \\ P \cdot T \\ Q \cdot D \end{bmatrix}\\$

其中 $P = (D \times E_2), Q = (T \times E_1)$ .

所以整个计算就是我们无需再去计算三角形平面的一些性质，取而代之我们用以上式子就可以计算出 t, u, v.

// OD: ray, p0p1p2: triangle bool ray_triangle_intersect_mt(const Vec3f O, const Vec3f D, const Vec3f p0, const Vec3f p1, const Vec3f p2, float &t, float &u, float &v){ Vec3f e1 = p1-p0; Vec3f e2 = p2-p0; Vec3f pvec = cross(D, e2); float det = e1*pvec; if (det < epsilon) return false; Vec3f tvec = O - p0; u = tvec*pvec*(1./det); if (u < 0 || u > 1) return false; Vec3f qvec = cross(tvec, e1); v = D*qvec*(1./det); if (v < 0 || u + v > 1) return false; t = e2*qvec*(1./det); return t > epsilon; }

直线与三角形相交是如此重要，是因为有了这些算法，在‘光线追踪’中，我们可以放model来玩，同时在 ‘光栅化’中，利用三角形的重心坐标来做各种插值也算光栅化的基石之一。

代码：

KrisYu/miscellaneous

参考：

Fast, minimum storage ray-triangle intersection.

Ray Tracing: Rendering a Triangle

上一篇： zd03 3(2)

下一篇：爬虫数据抓取软件

版权声明：
本文来源网络，所有图片文章版权属于原作者，如有侵权，联系删除。

本文网址：https://www.mushiming.com/mjsbk/5729.html

相关文章：