说明:算法源自教材。本文相当于对教材做的一个笔记
首先:动态规划能够成立的前提是:原问题具备重叠子问题和最优子结构的性质
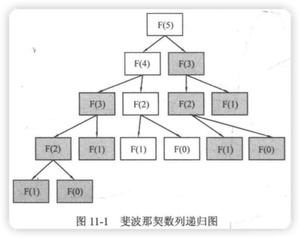
重叠子问题:存在子问题会被重复计算多次。以经典的斐波拉契数列F(n)=F(n - 1)+F(n - 2)为例:求解f5原问题时,子问题f2被重复求解了3次。
最优子结构:子问题相互独立且子问题的最优解可以推出原问题的最优解(局部最优可以推出全局最优:f1,f2的解可以推出f3的解,且f1不会影响f2)。举一个生活中的例子,引用自
比如说,假设你考试,每门科目的成绩都是互相独立的。你的原问题是考出最高的总成绩,那么你的子问题就是要把语文考到最高,数学考到最高…… 为了每门课考到最高,你要把每门课相应的选择题分数拿到最高,填空题分数拿到最高…… 当然,最终就是你每门课都是满分,这就是最高的总成绩。
得到了正确的结果:最高的总成绩就是总分。因为这个过程符合最优子结构,“每门科目考到最高”这些子问题是互相独立,互不干扰的。
但是,如果加一个条件:你的语文成绩和数学成绩会互相制约,数学分数高,语文分数就会降低,反之亦然。这样的话,显然你能考到的最高总成绩就达不到总分了,按刚才那个思路就会得到错误的结果。因为子问题并不独立,语文数学成绩无法同时最优,所以最优子结构被破坏。
动态规划算法:
动态规划就是一个填表的过程。该表记录了已解决的子问题的答案。求解下一个子问题时会用到上一个子问题的答案。{比如01背包问题:假如有1个背包,背包容量是10,有5个物品,编号为1,2,3,4,5,他们都有各自的重量和价格。要求在不超过背包容量的情况下,使背包装载物品的价值最大。现将问题拆分为五个子问题。
1.背容=10,从1号物品中找出该问题的解
2.背容=10,从1号,2号物品中找出该问题的解
3.背容=10,从1号,2号,3号物品中找出该问题的解
4.背容=10,从1号,2号,3号,4号物品中找出该问题的解
5.背容=10,从1号,2号,3号,4号,5号物品中找出该问题的解
}
思路:
我们可以将1,2,3,4,5子问题的答案都存入一张表中。因为求解2子问题,需要用到1子问题的答案(2的每一步方案要与1的每一步方案比较,如何2的该步方案优于1所对应的方案。则将2的这步方案标为可行。如果不优于1的,或者不满足问题的约束条件,则舍弃该方案。继续沿用该步所对应的1的方案作为该步的方案)。求解3子问题,需要用到2子问题的答案,一直递推到求解5子问题,需要用到4子问题的答案。而5子问题就是原问题。5子问题的答案就是最终原问题的解。
解法:
以01背包问题为例,作讲解。给出问题参数:
运行的最终结果是张二维表:(f[i][j],i就是n,j就是c)
填表相关说明:
1.程序是一行一行的进行填表的。f[0][0,1,2,3,4.....]......f[5][0,1,2,3,4....] (程序初始化的过程就是将第0行的所有数填为0,这是符合现实情况的。它表明当前背包没有装物品,当前背包的价值是0)
2.拿f[3][8]=11来说明填表的过程。f[3]表明i=3(当前子问题有3个物品可选,分别是1,2,3号物品),f[3][*]的值就是第3个子问题的解。我要选的3号物品的重量是6,它的价值是5,所以我会找到它的前6列的上一行所对应的背包的价值(f[2][2])+5(当前要选的3号物品的价值)=11,值为11>f[2][8]=9,代表我选了1,3的方案要优于选1,2的这种方案,所以我将11填入到表格【如果f[2][2]+5<9,则将9填入表格】-------------------这里需要说明一下f[2][8]=9的含义:2子问题的一个解是{1,2}选择1,2号物品所对应的背包价值为9。------恰巧我们在解决3子问题时{1,2,3}需要计算比较这几种方案,选1,2号物品{1,2}>>>>背价=?,背包价格是多少,{1,3}>>>>背价=?,{1,2,3}>>>>背价=?而{1,2}>>背包价格在2子问题中已给出,因此我们可以在3子问题中直接用。为何不考虑{2,3}呢?就是拿2号和3号组队放入背包?因为在2子问题中已经记载了:【如果要单选一个背包的话,选择1号获得的价值要比2号获得的价值大----我们追溯到f[2][2]=6是整么来的,背包容量是2的时候,[1,2]号物品只能有一个放入背包,放入1,背包的价值是6,f[1][2]=6的计算是在1子问题中已经求解出来的,2子问题可以直接用该值,而不用再重复计算。放入2号,背值是3,3<6,所以沿用上一个子问题的解作为该步的答案,所以f[2][2]是6,而不是3,所以它相当于定义说:下一个子问题在求解的过程中,如果遇到只能从2号和1号物品中选择一个物品装入背包时,请选择1号物品】
3.其实将上述的描述写成代码,就是两层for循环(遍历n,再嵌套遍历c),加上两个判断(1.当前子问题的可行的一个方案与上一个子问题的对应的可行方案谁最优。2.连续变量j的值是否达到了跳跃点的值,达到了才更新当前背包的价值):代码如下
如何进一步优化算法:
上述算法有两个明显的缺点:
其一是算法要求所给物品的重量w[i]是整数.
其次,当背包容量很大时,算法需要的计算时间较多,当c>2^n,算法需要n*2^n这么多的计算时间.
优化思路:
仔细观察,发现该二维表的值,是关于物品背包当前背包容量的阶梯状函数,并且它是一个阶梯状,单调不减函数,所以我们可以通过构造跳跃点集的方式来优化算法。其相关说明如下:
程序运行的数据流图如下:
最后放一下优化后的算法的代码实现:
补充:
(2) 分治与动态规划——重叠子问题
相同点:
将问题分解成子问题,然后合并子问题的解得到原问题的解。
不同点:
分治法解决的问题不拥有重叠子问题,解决的问题不一定是最优化问题;
动态规划解决的问题拥有重叠子问题,解决的问题一定是最优化问题。
(2) 贪心与动态规划——最优子结构
相同点
都要求原问题必须拥有最优子结构。
不同点
贪心的计算方式类似于”自顶向下“,但是并不等待所有子问题求解完毕后再选择使用哪一个,而是通过一种策略直接选择一个子问题去求解,没被选择的子问题就不会再去求解了。
动态规划的计算方式有”自顶向下“和”自底向上“两种,都是从边界开始向上得到目标问题的解。也就是说,它总是会考虑所有子问题,并选择继承能得到最优结果的那个,对暂时没有被继承的子问题,由于重叠子问题的存在,后期可能会再次考虑它们,因此还有机会成为全局最优的一部分,不需要放弃。
如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样,但它们具有相同的填表格式
后记:
算法的时间复杂度分析: 优化前:O(nc) 优化后:O(min{nc,2^n})
上述问题不知道我描述清楚否,记录的是否有误。欢迎在评论区留言。我们一起学算法
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/5416.html
