参考来源:和感谢
1.代码随想录 (programmercarl.com)
2.【图-最小生成树-Prim(普里姆)算法和Kruskal(克鲁斯卡尔)算法】https://www.bilibili.com/video/BV1wG411z79G?vd_source=0ddb24a0baa69b0b871ab50f7
3.【图-最短路径-Dijkstra(迪杰斯特拉)算法】https://www.bilibili.com/video/BV1uT4y1p7Jy?vd_source=0ddb24a0baa69b0b871ab50f7
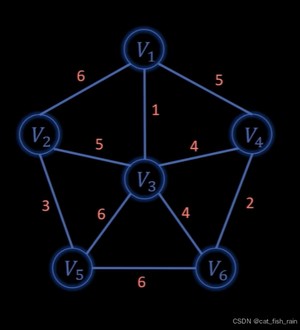
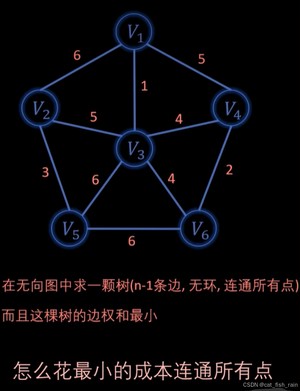
最小生成树是所有节点的最小连通子图, 即:以最小的成本(边的权值)将图中所有节点链接到一起。图中有n个节点,那么一定可以用 n - 1 条边将所有节点连接到一起。那么如何选择 这 n-1 条边 就是 最小生成树算法的任务所在。
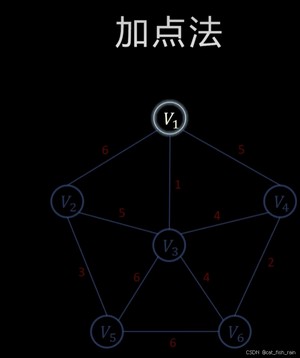
1.随便初始化一条边,因为需要所有的结点都需要连接,任何节点都可以。一般默认index=0的结点。
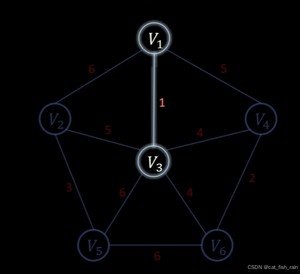
2.找到非生成树(已经连接的部分)到生成树(已经连接部分)最小权重的边,进行连接。
3.更新生成树和非生成树的 距离,并进行连接,重复以上过程。直至全部连接完毕。
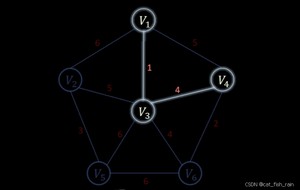
prim算法 是从节点的角度 采用贪心的策略 每次寻找距离 最小生成树最近的节点 并加入到最小生成树中。
prim算法核心就是三步:
- 第一步,选距离生成树最近节点
- 第二步,最近节点加入生成树
- 第三步,更新非生成树节点到生成树的距离(即更新minDist数组)
题目:
在世界的某个区域,有一些分散的神秘岛屿,每个岛屿上都有一种珍稀的资源或者宝藏。国王打算在这些岛屿上建公路,方便运输。
不同岛屿之间,路途距离不同,国王希望你可以规划建公路的方案,如何可以以最短的总公路距离将 所有岛屿联通起来。
给定一张地图,其中包括了所有的岛屿,以及它们之间的距离。以最小化公路建设长度,确保可以链接到所有岛屿。
输入描述:
第一行包含两个整数V 和 E,V代表顶点数,E代表边数 。顶点编号是从1到V。例如:V=2,一个有两个顶点,分别是1和2。
接下来共有 E 行,每行三个整数 v1,v2 和 val,v1 和 v2 为边的起点和终点,val代表边的权值。
输出描述:
输出联通所有岛屿的最小路径总距离
示例:
输出
输出示例:
6
代码:
给出一个有向图,一个起点,一个终点,问起点到终点的最短路径。
接下来,我们来详细讲解最短路算法中的 dijkstra 算法。
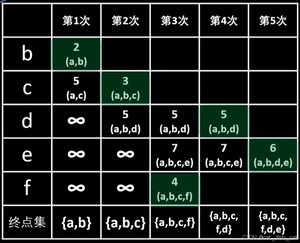
dijkstra算法:在有权图(权值非负数)中求从起点到其他节点的最短路径算法。
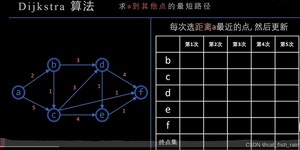
ijkstra 算法 同样是贪心的思路,不断寻找距离 源点最近的没有访问过的节点。
这里我也给出 dijkstra三部曲:
- 第一步,选源点到哪个节点近且该节点未被访问过
- 第二步,该最近节点被标记访问过
- 第三步,更新非访问节点到源点的距离(即更新minDist数组)
题目
小明是一位科学家,他需要参加一场重要的国际科学大会,以展示自己的最新研究成果。
小明的起点是第一个车站,终点是最后一个车站。然而,途中的各个车站之间的道路状况、交通拥堵程度以及可能的自然因素(如天气变化)等不同,这些因素都会影响每条路径的通行时间。
小明希望能选择一条花费时间最少的路线,以确保他能够尽快到达目的地。
【输入描述】
第一行包含两个正整数,第一个正整数 N 表示一共有 N 个公共汽车站,第二个正整数 M 表示有 M 条公路。
接下来为 M 行,每行包括三个整数,S、E 和 V,代表了从 S 车站可以单向直达 E 车站,并且需要花费 V 单位的时间。
【输出描述】
输出一个整数,代表小明从起点到终点所花费的最小时间。
输入示例
输出示例:12
代码实现。
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/4403.html
