了解图像增强的目的及意义,加深对图像增强的感性认知
1. 掌握直接灰度变换的图像增强方法
2. 掌握灰度直方图的概念及其计算方法
3. 掌握直方图均衡化合直方图规定化得计算过程
- 利用临域平均法,临域加权平均法,中值滤波对图像进行滤波处理
- 掌握彩色图像的滤波处理
- 利用梯度方法对图像进行锐化处理
- 结合图像的平滑和锐化增强图像
对二维的傅立叶变换有一定的认识,了解图像中傅立叶变换的意义 。
图像增强的方法是通过一定手段对原图像附加一些信息或变换数据,有选择地突出图像中感兴趣的特征或者抑制(掩盖)图像中某些不需要的特征,使图像与视觉响应特性相匹配。
三. 实验内容及结果分析。图像增强是从像素到像素的操作,是以预定的方式改变图像的灰度直方图。有时又称为对比度增强,灰度变换。点运算不可能改变图像内的空间关系,输出像素的灰度值由输入像素的值决定。其作用:对比度增强:扩展感兴趣特征的对比度。
首先,解释下什么是对比度:通俗的讲,就是明暗的对比程度,通常表现了图像画质的清晰程度,实际上,对比度反映了一幅图像中明暗区域最亮的白和最暗的黑之间不同亮度层级的测量,即指一幅图像灰度反差的大小,差异范围越大代表对比越大,差异范围越小代表对比
越小,好的对比率120:1就可容易地显示生动、丰富的色彩,当对比率高达300:1时,便可支持各阶的颜色。但对比率遭受和亮度相同的困境,现今尚无一套有效又公正的标准来
衡量对比率,所以最好的辨识方式还是依靠使用者眼睛。
直方图均衡化处理的“中心思想”是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布。直方图均衡化就是对图像进行非线性拉伸,重新分配图像像素值,使一定灰度范围内的像素数量大致相同。直方图均衡化就是把给定图像的直方图分布改变成“均匀”分布直方图分布。缺点:
1)变换后图像的灰度级减少,某些细节消失;
2)某些图像,如直方图有高峰,经处理后对比度不自然的过分增强。
直方图均衡化是图像处理领域中利用图像直方图对对比度进行调整的方法。
这种方法通常用来增加许多图像的局部对比度,尤其是当图像的有用数据的对比度相当接近的时候。通过这种方法,亮度可以更好地在直方图上分布。这样就可以用于增强局部的对比度而不影响整体的对比度,直方图均衡化通过有效地扩展常用的亮度来实现这种功能。
这种方法对于背景和前景都太亮或者太暗的图像非常有用,这种方法尤其是可以带来X光图像中更好的骨骼结构显示以及曝光过度或者曝光不足照片中更好的细节。这种方法的一个主要优势是它是一个相当直观的技术并且是可逆操作,如果已知均衡化函数,那么就可以恢复原始的直方图,并且计算量也不大。这种方法的一个缺点是它对处理的数据不加选择,它可能会增加背景杂讯的对比度并且降低有用信号的对比度。
直方图均衡化的基本思想是把原始图的直方图变换为均匀分布的形式,这样就增加了象素灰度值的动态范围从而可达到增强图像整体对比度的效果。
设r和s人别表示原图像灰度级和经过直方图均衡化后的图像灰度级。为便于讨论,对r和s进行归一化,使 对于一幅给定的图像归一化后灰度级分布在 范围内。对[0, 1]区间内的任何一个值进行如下变换:
该变换应该满足条件
1)对于
,有
2)在
区间内设r的概率密度为
,s的概率密度可由
求出
假设变换函数为
式中:w是积分变量,而
就是r的累积分布函数。
离散形式的直方图均衡化
设一幅图像的像元数为n,公有m个灰度级,
代表灰度级为r的像元的数目,则第k个灰度级出现的概率可表示为:
变换函数 改写为:
均衡化后的图像灰度值可直接由原图像的直方图算出。
在实际应用中,希望能够有目的地增强某个灰度区间的图像, 即能够人为地修正直方图的形状, 使之与期望的形状相匹配,这就是直方图规定化的基本思想。换句话说,希望可以人为地改变直方图形状,使之成为某个特定的形状,直方图规定化就是针对上述要求提出来的一种增强技术,它可以按照预先设定的某个形状来调整图像的直方图。直方图规定化是在运用均衡化原理的基础上,通过建立原始图像和期望图像之间的关系,选择地控制直方图,使原始图像的直方图变成规定的形状,从而弥补了直方图均衡不具备交互作用的特性。
直方图规定化步骤:
1. 其增强原理是先对原始的直方图均衡化:S = T(r)
2. 找到一种映射有原来的直方图映射到新的目的直方图。
3. 将规定化的直方图进行均衡化。v = G(z)
3. 由于都是均衡化,故令 S = v,则:z = G-1(v) = G-1[T(r)]
图像平滑是指用于突出图像的宽大区域、低频成分、主干部分或抑制图像噪声和干扰高频成分,使图像亮度平缓渐变,减小突变梯度,改善图像质量的图像处理方法。图像平滑的方法包括:插值方法,线性平滑方法,卷积法等等。这样的处理方法根据图像噪声的不同进行平滑,比如椒盐噪声,就采用线性平滑方法!
均值滤波器(averaging filter)是消除噪声的最简单的方法。原理:使用某像素周围mxn像素范围内的平均值来置换该像素值。通过使图像模糊,达到看不到细小噪声的目的。不良反应:使用这种方法,在噪声被消除的同时,目标图像也变模糊了。
在图像增强过程中,通常利用各类图像平滑算法消除噪声,图像的常见噪声主要有加性噪声、乘性噪声和量化噪声等。一般来说,图像的能量主要集中在其低频部分,噪声所在的频段主要在高频段,同时图像边缘信息也主要集中在其高频部分。这将导致原始图像在平滑处理之后,图像边缘和图像轮廓模糊的情况出现。为了减少这类不利效果的影响,就需要利用图像锐化技术,使图像的边缘变得清晰。图像锐化处理的目的是为了使图像的边缘、轮廓线以及图像的细节变得清晰,经过平滑的图像变得模糊的根本原因是因为图像受到了平均或积分运算,因此可以对其进行逆运算(如微分运算)就可以使图像变得清晰。微分运算是求信号的变化率,由傅立叶变换的微分性质可知,微分运算具有较强高频分量作用。从频率域来考虑,图像模糊的实质是因为其高频分量被衰减,因此可以用高通滤波器来使图像清晰。但要注意能够进行锐化处理的图像必须有较高的性噪比,否则锐化后图像性噪比反而更低,从而使得噪声增加的比信号还要多,因此一般是先去除或减轻噪声后再进行锐化处理。
2.4 图像锐化的几种方式
1) 水平竖直直梯度
2) Robert 梯度
3) Sobel 算子
4) 二阶梯度
在图像处理中,一阶微分是通过梯度算法来实现的,对于一幅图像用函数f(x,y)表示,定义在f(x,y)在点(x,y)处的梯度是一个矢量,定义为:
梯度的方向在函数f(x,y)最大变化率的方向上,梯度的幅度G[f(x,y)]可以由以下公式算出:
由上式可知:梯度的数值就是f(x,y)在其最大变化率方向上的单位距离所增加的量。对于数字图像而言,微分可用差分来近似。因此上式可以写成:
这种方法就是上面的水平竖直梯度法。
彩色图像平滑处理和灰度图像的平滑处理类似,差别在于彩色图像需要对各个通道依次进行平滑操作,使得每一个通道对应的图像都经过平滑处理,时间复杂度要远比灰度图像的高。还有就是彩色图像的噪声和灰度图的噪声有所差别,有时候需要区别的对待。
傅里叶提出任何周期函数都可以表示为不同频率的正弦和/或余弦和的形式,每个正弦和/或余弦乘以不同的系数(傅里叶级数)。图像的频率是表征图像中灰度变化剧烈程度的指标,是灰度在平面空间上的梯度.在噪声点和图像边缘处的频率为高频。
傅立叶变换在实际中有非常明显的物理意义,设f是一个能量有限的模拟信号,则其傅立叶变换就表示f的谱。从纯粹的数学意义上看,傅立叶变换是将一个函数转换为一系列周期函数来处理的。从物理效果看,傅立叶变换是将图像从空间域转换到频率域,其逆变换是将图像从频率域转换到空间域。换句话说,傅立叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数,傅立叶逆变换是将图像的频率分布函数变换为灰度分布函数.
傅立叶变换以前,图像(未压缩的位图)是由对在连续空间(现实空间)上的采样得到一系列点的集合,我们习惯用一个二维矩阵表示空间上各点,则图像可由z=f(x,y)来表示。由于空间是三维的,图像是二维的,因此空间中物体在另一个维度上的关系就由梯度来表示,这样我们可以通过观察图像得知物体在三维空间中的对应关系。为什么要提梯度?因为实际上对图像进行二维傅立叶变换得到频谱图,就是图像梯度的分布图,当然频谱图上的各点与图像上各点并不存在一一对应的关系,即使在不移频的情况下也是没有。傅立叶频谱图上我们看到的明暗不一的亮点,实际上图像上某一点与邻域点差异的强弱,即梯度的大小,也即该点的频率的大小(可以这么理解,图像中的低频部分指低梯度的点,高频部分相反)。一般来讲,梯度大则该点的亮度强,否则该点亮度弱。这样通过观察傅立叶变换后的频谱图,也叫功率图,我们首先就可以看出,图像的能量分布,如果频谱图中暗的点数更多,那么实际图像是比较柔和的(因为各点与邻域差异都不大,梯度相对较小),反之,如果频谱图中亮的点数多,那么实际图像一定是尖锐的,边界分明且边界两边像素差异较大的。对频谱移频到原点以后,可以看出图像的频率分布是以原点为圆心,对称分布的。将频谱移频到圆心除了可以清晰地看出图像频率分布以外,还有一个好处,它可以分离出有周期性规律的干扰信号,比如正弦干扰,一副带有正弦干扰,移频到原点的频谱图上可以看出除了中心以外还存在以某一点为中心,对称分布的亮点集合,这个集合就是干扰噪音产生的,这时可以很直观的通过在该位置放置带阻滤波器消除干扰。
图像是两个参数的函数,通过一组正交函数的线性组合可以将其分解,而傅里叶就是通过谐波函数来分解的。而对于离散傅里叶变换,傅里叶变换的条件是存在的。
傅里叶变换进行图像处理有几个特点
1. 直流成分F(0,0)等于图像的平均值;
2. 能量频谱|F(u,v)|^2完全对称于原点;其中F=PfQ, f表示原图,P和Q都是对称的实正交矩阵,这个公式表示傅里叶变换就是个正交矩阵的正交变换
3.图像f平移(a,b)后,F只有exp[-2pij(au/M+bv/M)]的相位变化,能量频谱不发生变化。
4. 图像f自乘平均等于能量频谱的总和,f的分散等于能量频谱中除直流成分后的总和。
5.图像f(x,y)和g(x,y)的卷积h(x,y)=f(x,y)*g(x,y)的傅里叶变换H(u,v)等于f(x,y)和g(x,y)各自的傅里叶变换的乘积。
图像中的每个点通过傅里叶变换都成了谐波函数的组合,也就有了频率,这个频率则是在这一点上所有产生这个灰度的频率之和,也就是说傅里叶变换可以将这些频率分开来。当想除去图像背景时,只要去掉背景的频率就可以了。
通常在进行傅里叶变换之前用(-1)^(x+y)乘以输入的图像函数,这样就可以将傅里叶变换的原点F(0,0)移到(M/2,N/2)上。
每个F(u,v)项包含了被指数修正的f(x,y)的所有值,因而一般不可能建立图像特定分量和其变换之间的联系。然而,一般文献通常会有关于傅里叶变换的频率分量和图像空间特征之间联系的阐述。变换最慢的频率成分(u=v=0)对应一幅图像的平均灰度级。当从变换的原点移开时,低频对应着图像的慢变换分量,较高的频率开始对应图像中变化越来越快的灰度级。这些事物体的边缘和由灰度级的突发改变(如噪声)标志的图像成分。
从文件中读取一幅图像,转换成灰度图,将其进行均衡化处理,最后对比原始灰度图和均衡化后的结果。
下面的函数是我自己写的均衡化操作函数
核心函数:
这个函数是自己编写的一个将原始图像进行直方图均衡化的函数。

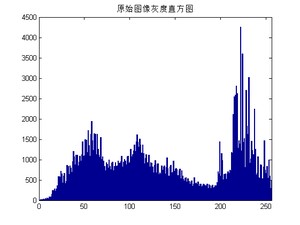

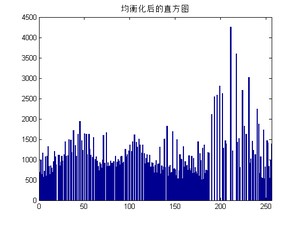
从均衡化后的结果可以看出来,图像的对比度略有提升,对应的直方图的分布也相对均匀。但缺点是某些像素值是没有的,也就是灰度值少了一些。
直方图规定化是给出一个映射使直方图按所需映射要求进行变换, 测试程序的代码如下所示:
“`
1. I = imread(‘123.jpg’);
2. I = rgb2gray(I);
3. hgram=0:255;
4. J = histeq(I,hgram);
5. figure(),imshow(I),title(‘原始图像’);
6. figure(), imshow(J),title(‘直方图规定化后图像’);
7. figure(), imhist(I),title(‘原始图像直方图’);
8. figure(), imhist(J),title(‘规定化后图像直方图’);
““
效果如下图所示

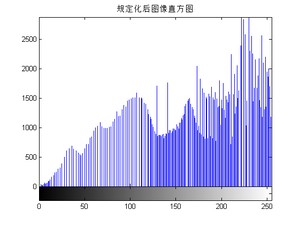
邻域均值滤波效果如下:



从上述三幅图像中我们可以看出利用均值滤波函数进行去除高斯噪声是有一定效果的,图2.2和图2.3 都明显有去噪效果。此外,3×3模板和5×5模板效果也会略有差异,从图中看出5×5模板明显失去了一些图像细节。
中值滤波效果如下


通过两幅图片的对比我们可以看出来,中值滤波对于椒盐噪声的去除效果非常明显,经过中值滤波操作,像基本不会有椒盐噪声的存在。
水平数值一阶梯度上面原理已经说过,下面列出我写的代码,输入参数pic为待处理的图像矩阵,varargin表示可选的阈值参数,得到的梯度值大于这个值则梯度值赋为255,否则赋为0,这样可以更清楚地对图像的边缘进行表现。
用一阶的水平竖直梯度进行图像锐化的效果如下图所示


从图中的对比中我们发现图像中具有明显边界的区域很明显地被识别出来,即在图像中轮廓的边界往往蕴含着梯度信息。
Robert梯度旨在寻找不仅仅水平和竖直两个方向的梯度,所以Robert表示为斜向的梯度。下面是我写的关于Robert梯度计算的函数RobertGradient(pic, varargin),同样的,pic表示原始图像矩阵,varargin表示可选的阈值参数,默认为40,当得到的梯度模大于40,对应的像素点的值为255,否则为0。
Robert梯度的算法效果如下:

Sobel算子根据像素点上下、左右邻点灰度加权差,在边缘处达到极值这一现象检测边缘。对噪声具有平滑作用,提供较为精确的边缘方向信息,边缘定位精度不够高。当对精度要求不是很高时,是一种较为常用的边缘检测方法。下面是我写的Sobel算子进行锐化的函数。
Sobel的算法效果如下图所示:

Sobel边缘检测的结果能用线条较好地描述图像,源图像中对比度较高的区域在结果图中体现为高灰度的像素,简单地说就是对源图像进行了“描边”操作。在进行图像细化时,最直接的思路就是对线条宽度进行缩减,然而图像中的线条往往是不规则的,这使得直接对线条进行处理的方法很难实现。
从上面三种图像锐化操作的结果对比中我们可以看出水平竖直梯度和Robert梯度的锐化效果近似,但对比于Sobel算子,他们在细节上有很明显的缺失。Sobel感觉上图像的边缘信息不仅仅被提取出来而且进一步被细化。
图像的傅立叶变换
图像的傅立叶变换,原始图像由N行N列构成,N必须是基2的,把这个N*N个包含图像的点称为实部,另外还需要N*N个点称为虚部,因为FFT是基于复数的。计算图像傅立叶变换的过程很简单:首先对每一行做一维FFT,然后对每一列做一维FFT。具体来说,先对第0行的N个点做FFT(实部有值,虚部为0),将FFT输出的实部放回原来第0行的实部,FFT输出的虚部放回第0行的虚部,这样计算完全部行之后,图像的实部和虚部包含的是中间数据,然后用相同的办法进行列方向上的FFT变换,这样N*N的图像经过FFT得到一个N*N的频谱。
实验内容分析
下面我们进行在频域进行图像压缩的实验,实验方法是将图像进行二维的傅立叶变换,然后在频域矩阵中去掉某些频率的值这样使得原本的图像失去一些对应频率的基向量,从而达到数据压缩的效果。这里我们在频域中利用图像像素乘法的思想对频域图像进行压缩,让ROI区域以外的幅度值变为0,ROI部分的区域值不变,最后进行反傅立叶变化,实现图像的压缩变换。这种压缩变换往往是不可逆的,所以并不属于无失真压缩方法。本实验中ROI的选取是以图像中心做为圆心,以指定数值为半径做的圆作为实验中的ROI。
实验的代码
实验结果
首先原始图像是一只可爱的猫咪如下图:

将上述图像进行傅立叶变换得到


上图分别表示傅立叶变换后图像的实部和傅立叶变换后的虚部。
下面将通过选取不同的ROI区域对原图像进行压缩变换,最后对比结果。


从结果图中可以看出图像经过这样的压缩变换后仅仅能大致看清事物的轮廓,其他细节部分已经完全分辨不出。通过上述实验我们实践了通过傅立叶变换进行压缩变换的原理,并且认识到傅立叶变换在信号及图像处理中具有重要意义。
已经做过四次实验报告了,看着自己写的一些完成一些图像处理的基础算法还是有一点小成就感呢,似乎有点小激动,不过最大的感慨就是,知识和实践相结合是一件非常美妙的事,实践能帮助增强对知识本身的理解,知识推动者实践的热情。无论学习也好,科研也罢,尽自己最大的努力去争取,去探索,我相信我们成功的概率一定会越来越大的。
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/4232.html
