树状数组 线段树



@

树状数组(Binary Indexed Tree(B.I.T), Fenwick Tree)是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有元素之和，但是每次只能修改一个元素的值;经过简单修改可以在log(n)的复杂度下进行范围修改，但是这时只能查询其中一个元素的值(如果加入多个辅助数组则可以实现区间修改与区间查询)。

树状数组，重点在于它是树状的 （这不废话吗）
大家都知道二叉树吧，贴一张二叉树的图给大家理解一下（自己画的有点丑）

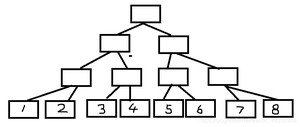
我们把它变形一下...

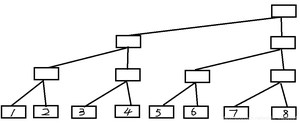
现在定义每一列的顶端结点C[]数组

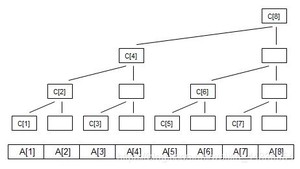
ps.最后一个图不是我画的

C[i]代表子树的叶子结点的权值之和， 这里以求和举例

如图可以知道

C[1]=A[1];

C[2]=A[1]+A[2];

C[3]=A[3];

C[4]=A[1]+A[2]+A[3]+A[4];

C[5]=A[5];

C[6]=A[5]+A[6];

C[7]=A[7];

将C[]数组的结点序号转化为二进制

1=(001) C[1]=A[1];

2=(010) C[2]=A[1]+A[2];

3=(011) C[3]=A[3];

4=(100) C[4]=A[1]+A[2]+A[3]+A[4];

5=(101) C[5]=A[5];

6=(110) C[6]=A[5]+A[6];

7=(111) C[7]=A[7];

8=(1000) C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

对照式子可以发现 C[i]=A[i-2^ k+1]+A[i-2^k+2]+......A[i];
（k为i的二进制中从最低位到高位连续零的长度）例如i=8时，k=3;

可以自行带入验证;

现在引入lowbit(x)

lowbit(x) 其实就是取出x的最低位1 换言之 lowbit(x)=2^k k的含义与上面相同 理解一下

前两个普通数组能够O(1)时间复杂度完成，后两个普通数组需要O(n)时间复杂度完成，而树状数组最大只需要O(logn)，这也正是树状数组的快捷之处。

代码实现

0.lowbit操作

版权声明：

本文来源网络，所有图片文章版权属于原作者，如有侵权，联系删除。

本文网址：https://www.mushiming.com/mjsbk/3894.html