01背包问题动态规划详解



比如现在有四个物品，要把这四个物品放入一个容量为8的背包之中，然后现在要求这个背包最大能够放入价值为多少的物品？

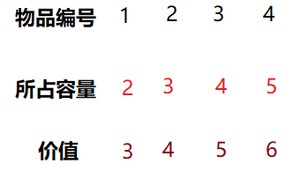
接下来第一件事就是列表，不要问为什么，就是这个方法，这张表是至底向上，从左到右生成的。

首先第一行第一列

因为背包容量为0无法放入物品所以第一列的最大价值就全为0；
物体编号为0意味着放入前0个物品，也就是不放入物品，所以第一行的最大价值就全为0

填写第一行

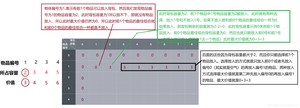
填写第二行

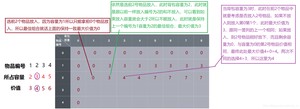
以此类推写完全部
拿最后一个举例看看背包内价值最大的情况下，背包内装了哪些物品

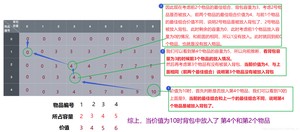
解法归纳：
一、如果装不下当前物品
那么前n个物品的最佳组合和前n-1个物品的最佳组合是一样的。

二、如果装得下当前物品
假设1：
装当前物品，在给当前物品预留了相应空间的情况下，前n-1个物品的最佳组合加上当前的价值就是总价值

假设2：
不装当前物品，那么前n个物品的最佳组合和前n-1个物品的最佳组合是一样的。
选取假设1和假设2中的较大的价值，为当前的最佳组合的价值。

如果你看懂了以上的所有的流程，那现在下面这个式子就可以理解了。
01背包的状态转换方程 f[i,j] = Max{ f[i-1,j-Wi]+Pi( j >= Wi ), f[i-1,j] }

f[i,j]表示在前i件物品中选择若干件放在承重为 j 的背包中，可以取得的最大价值。
Pi表示第i件物品的价值。

回溯：
从表的右下角开始回溯，如果发现前n个物品最佳组合的价值和前n-1个物品最佳组合的价值一样，说明第n个物品没有被装入，否则第n个物品被装入

版权声明：

本文来源网络，所有图片文章版权属于原作者，如有侵权，联系删除。

本文网址：https://www.mushiming.com/mjsbk/3766.html