C语言是一种很奇妙的语言,它既有高级语言的特点,又有低级语言的特点,支持位运算让它更方便于硬件编程。
一、左移运算符(<<)
左移运算就是将一个二进制位的操作数按指定位数整体向左移位,移出位被丢弃(是否丢弃也不一定,得看接收结果的数据类型范围),右边的空位一律补0。

语法:x << n,其中 x 是要移动的数字,n 是要移动的位数。
关联的数学公式:位左移结果 = 要移动的数字 * 2的n次方(n 是要移动的位数)。该公式不是总有效啊!
1、正数左移举例:
完整代码在后面。
这里我们用char类型,因为它范围是1个字节,8bit位,方便查看结果。
char ch = 10; // 00001010
// 左移1位
char r1 = ch << 1; // 00010100
printf("10 << 1 = %d ", r1); // 20 (10*2的1次方)
结果如下:
// 左移2位
char r2 = ch << 2; // 00
printf("10 << 2 = %d ", r2); // 40 (10*2的2次方)
// 左移3位
char r3 = ch << 3; // 0
printf("10 << 3 = %d ", r3); // 80 (10*2的3次方)
==== 下面是重点 ====
左移4位-->关键地方到了,因为左移4位后最左边是1了,也就是说符号位为1,可能变负数了。
char r4 = ch << 4; // ,转换为十进制为 -32,但真的是-32吗?
printf("10 << 4 = %d ", r4);
结果如下:
答案是-96,正数左移真的有可能变成负数了,但为什么不是-32呢。
因为数值在内存中存储的是补码,正数的原码、反码、补码是一样的。负数的补码=原码取反+1。
我们对内存中的数左移时实际上都是对补码进行左移,实际取值时还要转换为原码的。
,符号位是1,负数,取原码时要先减去1,再取反才行。
- 1
-----------------
取反 -> -96
原码、反码、补码不懂的可以看我以前写的文章。
10 << 4 一定是负数吗?看下面代码
short r44 = ch << 4;
printf("10 << 4 = %d ", r44); // 160 (10*2的4次方)
怎么样,没变负数吧,也就是说左边移动的4位并没有被舍弃,这是因为我们用short类型来接收的,该类型为2个字节,你左移8位都能完整接收,更何况仅仅是左移4位了,因此不会舍弃。
完整代码如下:
2、负数左移举例:
注意:负数在内存中存储的是补码,对补码进行左移,再换算成原码才是我们要的结果。挺闹心的啊!但没办法,这不是我们能决定的。
char ch = -10; // 原码 --> 补码 (负数要看补码啊!!!!!!!!!)
// 左移1位
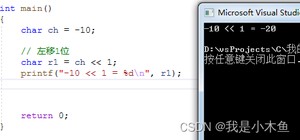
char r1 = ch << 1; // 补码 --> 原码
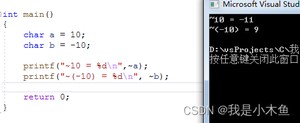
printf("-10 << 1 = %d ", r1); // -20 (-10*2的1次方)
结果如下:
// 左移2位
char r2 = ch << 2; // 补码 --> 原码
printf("-10 << 2 = %d ", r2); // -40 (-10*2的2次方)
// 左移3位
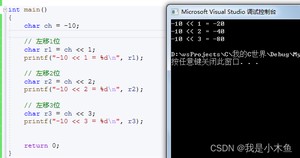
char r3 = ch << 3; // 补码 --> 原码
printf("-10 << 3 = %d ", r3); // -80 (-10*2的3次方)
结果如下:
======== 重点又到了 ========
左移4位-->关键地方又到了,因为左移4位后最左边是0了,也就是说符号位为0,可能变正数了。
char r4 = ch << 4; // 补码 0 --> 原码 0
printf("-10 << 4 = %d ", r4); // 96 (数学公式不好用了)
结果如下:
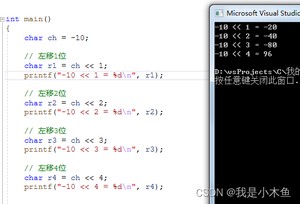
-10 << 4 一定是正数吗?看下面代码
short r44 = ch << 4;
printf("-10 << 4 = %d ", r44); // -160 (-10*2的4次方)
结果如下:
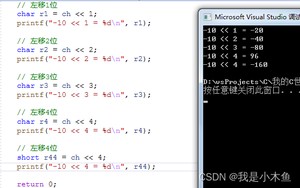
怎么样,没变正数吧,也就是说左边移动的4位并没有被舍弃,这是因为我们用short类型来接收的,该类型为2个字节,你左移8位都能完整接收,因此不会舍弃。
完整代码如下:
总结:左移运算时正数可能会变负数,负数也可能会变正数,左移的位数也未必舍弃,就看你用什么类型接收它,这个要注意啊。
二、右移运算符(>>)
右移运算就是将一个二进制位的操作数按指定位数整体向右移位,移出位被丢弃,左边的空位补符号位(还有一种情况是无论正负数都补0,这种情况不考虑,我们基本用不到)。
语法:x >> n,其中 x 是要移动的数字,n 是要移动的位数。
关联的数学公式:位右移结果 = 要移动的数字 / 2的n次方(n 是要移动的位数)。
1、正数右移举例:
// 这里我们用char类型,因为它范围是1个字节,8bit位,方便查看结果。
char ch = 10; // 00001010
// 右移1位
char r1 = ch >> 1; // 00000101
printf("10 >> 1 = %d ", r1); // 5 (10/2的1次方)
// 右移2位
char r2 = ch >> 2; // 00000010
printf("10 >> 2 = %d ", r2); // 2 (10/2的2次方,这里小数丢失精度了)
// 右移3位
char r3 = ch >> 3; // 00000001
printf("10 >> 3 = %d ", r3); // 1 (10/2的3次方)
// 右移4位
char r4 = ch >> 4; // 00000000
printf("10 >> 4 = %d ", r4); // 0
// 哪怕是我们用2个字节的short来接收结果也是一样的。
// 右移4位
short r44 = ch >> 4; // 00000000
printf("10 >> 4 = %d ", r44); // 0
结果如下:
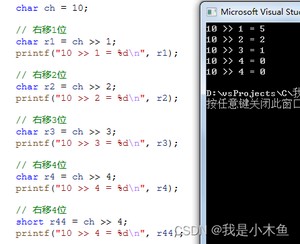
完整代码
2、负数右移举例:
// 注意:负数在内存中存储的是补码,对补码进行右移,再换算成原码才是我们要的结果。挺闹心的啊!但没办法,这不是我们能决定的。
char ch = -10; // 原码 --> 补码 (负数要看补码啊!!!!!!!!!)
// 右移1位
char r1 = ch >> 1; // 补码 --> 原码
printf("-10 >> 1 = %d ", r1); // -5 (-10/2的1次方)
// 右移2位
char r2 = ch >> 2; // 补码 --> 原码
printf("-10 >> 2 = %d ", r2); // -3 (-10/2的2次方)
// 右移3位
char r3 = ch >> 3; // 补码 --> 原码
printf("-10 >> 3 = %d ", r3); // -2 (-10/2的3次方)
// 右移4位
char r4 = ch >> 4; // 补码 --> 原码
printf("-10 >> 4 = %d ", r4); // -1 (-10/2的4次方)
// 右移4位(强转),不论正负数,右移时前面一律补0
char r44 = (unsigned char)ch >> 4; // 补码 =>转化为无符号类型,再右移4位,由于是无符号类型,前面补0 => 00001111
printf("(unsigned char)-10 >> 4 = %d ", r44); // 15
负数无论右移多少次,-1也就是到头了啊!
short a = -1207;
printf("-1207 >> 100 = %d ", -1207 >> 100); // -1
结果如下:
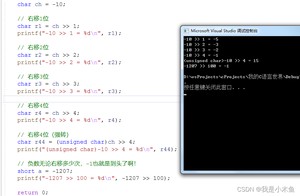
完整代码:
三、与运算符(&)
在编程中我们经常用到与运算符(&&),比如下面的代码:
if (1==1 && 2==2)
{
printf("这里用到与运算符,二者都为真才是真,否则为假! ");
}
这个与运算符(&&)是针对字节而言的,要是针对bit位而言与运算符就是(&)了。
与(&)是用来比较2个bit位的,二进制码只有0与1,我们认为0是假,1是真。只有全是真才是真,否则都为假。因此我们得到以下结论:
0 & 0 = 0;
0 & 1 = 0;
1 & 0 = 0;
1 & 1 = 1;
举个简单例子:
10 & 3 = ?
00001010 -> 10
& 00000011 -> 3
--------------------
00000010 -> 2
代码如下:
结果如下:

那么与(&)到底有什么用呢?
我们可以把二进制中的0与1当作电灯的开关(0-关灯,1-开灯),1个字节中的8bit当作8个开关,与(&)可以控制指定位置的开关为0,即关灯,其他位置不变。这点在电路上非常有用。
认识关羽吗?想要关灯(设置该bit位为0)吗?请用羽(与&),关二爷保佑你!
比如说:
二进制 0 1 0 0 1 1 0 1 -> 77(4D)
我想让其第1、4、5位置为0(从右往左数),其它位置不变,只要让77(4D)和数-26(E6)【该数的1、4、5为0,其他位置位1】做与运算即可。
0 1 0 0 1 1 0 1 -> 77 -> 4D
& 1 1 1 0 0 1 1 0 -> -26 -> E6 【,这里用一个字节来演示,最高位为1,则该数是负数,是补码,需要转变为原码才行。但如果我们用16进制E6来表示该数则不需要考虑负数的事,因此很多代码都是用16进制来进行与运算的。】
-------------------------------------------
0 1 0 0 0 1 0 0 -> 68 -> 44
结果如下:
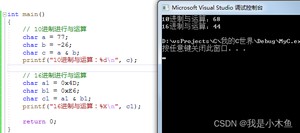
任何一个数与0做与(&)运算,结果一定是0。
四、或运算符(|)
在编程中我们经常用到或运算符(||),比如下面的代码:
if(1==1 || 2==3)
{
printf("这里用到或运算符,二者只要有一个为真结果就是真,否则为假! ");
}
这个或运算符(||)是针对字节而言的,要是针对bit位而言或运算符就是(|)了。
或(|)是用来比较2个bit位的,二进制码只有0或1,我们认为0是假,1是真。二者只要有一个为真结果就是真,否则为假!因此我们得到以下结论:
0 | 0 = 0;
0 | 1 = 1;
1 | 0 = 1;
1 | 1 = 1;
举个简单例子:
10 | 3 = ?
00001010 -> 10
| 00000011 -> 3
--------------------
00001011 -> 11
结果如下:
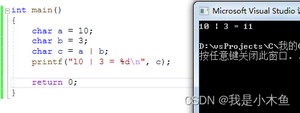
那么或(|)到底有什么用呢?
我们可以把二进制中的0或1当作电灯的开关(0-关灯,1-开灯),1个字节中的8bit当作8个开关,或(|)可以控制指定位置的开关为1,即开灯,其他位置不变。这点在电路上非常有用。
比如说:
二进制 0 1 0 0 1 1 0 1 -> 77(4D)
我想让其第2、6、8位置为1(从右往左数),其它位置不变,只要让77(4D)和数-94(A2)【该数的2、6、8为1,其他位置位0】做或运算即可。
0 1 0 0 1 1 0 1 -> 77 -> 4D
| 1 0 1 0 0 0 1 0 -> -94 -> A2 【,这里用一个字节来演示,最高位为1,则该数是负数,是补码,需要转变为原码才行。但如果我们用16进制来A2表示该数则不需要考虑负数的事,因此很多代码都是用16进制来进行或运算的。】
----------------------------------
1 1 1 0 1 1 1 1 -> -17 -> EF 【是负数的补码,转换为原码是-17】
代码如下:
结果如下:
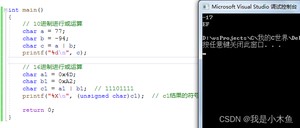
这里特意将符号位数字改为1,就是为了能练习一下负数的处理方式,否则用unsigned char变量会看起来更简单明了一些。
任何一个数与0做或(|)运算,结果一定是那个数。
五、异或运算符(^)
异或运算就是将二进制的两个操作数的每一位进行比较,如果相同结果为0,如果不同结果为1。它主要是看2个操作数是否有差异。就好像我们常玩的消消乐游戏,把一样的图案消掉,结果为0,不一样保留,结果就为1。
我们可以得出下面的结论:
0 ^ 0 = 0; // 一样,消消乐了
0 ^ 1 = 1; // 不一样,消不掉
1 ^ 0 = 1; // 不一样,消不掉
1 ^ 1 = 0; // 一样,消消乐了
举个简单例子:
10 ^ 3 = ?
00001010 -> 10
^ 00000011 -> 3
--------------------
00001001 -> 9
结果如下:
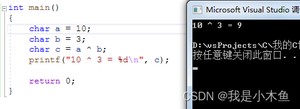
就是这么简单。
异或运算有一些很有意思的规律:
1) a ^ a = 0; // 自身异或,哪有差异性啊
2) a ^ 0 = a;
3) a ^ b ^ c = a ^ c ^ b = a ^ (b ^ c); // 乘法交换律与结合律啊
这里我们得出 a ^ b ^ a = a ^ a ^ b = 0 ^ b = b,该规律可以用于加密算法中。
举一些关于异或的小例子:
1、可以使用异或来交换两个变量的值(不允许创建第3个临时变量来帮忙)。
结果如下:
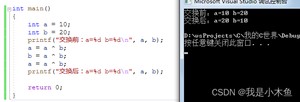
解析一下上面的代码,这里用a1,b1代表新的值;a,b代表原始值。
a = a ^ b; // 这里左边的a值已经改变了,我们称之为a1,b值未做改变。即 a1 = a ^ b;
b = a ^ b; // 这里代码相当于 b = a1 ^ b = a ^ b ^ b = a; b的值也改变了,我们称之为b1,此时存储的是a的原始值10,即 b1 = a。
a = a ^ b; // 这里代码相当于 a = a1 ^ b1 = a ^ b ^ a = b; a此时存储的是b的原始值20.
有点绕吧,哈哈!
2、利用异或加解密
结果如下:
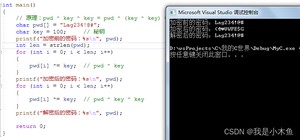
六、取反运算符(~)
取反很简单,就是二进制中的0变1,1变0。
~10 = ? // 10的取反是多少?
00001010 -> 10
~
--------------------
-> -11 --> 由于符号位是1,负数,这里是补码,得转换为原码才行。
~(-10) = ? // -10的取反是多少?
-> -10 这里存储的是-10的补码,原码是
~
--------------------
00001001 -> 9
结果如下:
常见综合案例
1、计算一个二进制数里有几个1?
我们用char类型举例,1个字节,方便查看结果。
显示结果:
代码解析:
for (int i = 0; i < 8; i++)
{
char a = (val >> i) & 1;
if (a == 1) { num++; }
arr[i] = a;
}
以-23举例,二进制是,因为是负数,所以内存中存储的是补码(原码取反+1),二进制的位运算没有遍历功能,因此我们将该二进制依次向右移1位,然后和1进行与(&)运算,将其前面的位都置为0,结果就是第1位上的值了,共右移8次即可。
>> 0
得到
& 00000001
-----------------------
00000001 --->这就是第1位上的值。
二进制就是这么遍历的。
2、消失的数字
代码解析:
这是关于异或的一道典型题,解题的原理是利用
0 ^ a = a // 0与任何数异或结果都是任何数
a ^ b ^ a = b // a ^ b ^ a = a ^ a ^ b = b,乘法的交换律
int arr[9] = {9,4,7,1,6,5,2,3,0};
int x = 0;
for (int i = 0; i < 9; i++)
{
x = x ^ arr[i] ^ i;
}
x ^= 9;
x = x ^ arr[i] ^ i; // 这个是重点也是难点
我们先不要每次循序都计算x的值,把式子都保留在一起最后计算,每次循环后积累的式子结果如下:
x = 0 ^ 9 ^ 0 ^ 4 ^ 1 ^ 7 ^ 2 ^ 1 ^ 3 ^ 6 ^ 4 ^ 5 ^ 5 ^ 2 ^ 6 ^ 3 ^ 7 ^ 0 ^ 8 ^ 9 // 补充x ^= 9;因为数组只有9个数,差1个。
上面是数组的9次循环再补充 ^= 9的式子展开结果。每次循环用不用颜色标记一下能看得清楚些。
异或就是消消乐,把相同的消掉,结果就是
x = 0 ^ 8 = 8 // OK
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/2805.html
