目录
⚽1.什么是二叉排序树
🏐2.构建二叉排序树
🏀3.二叉排序树的查找操作
🥎4.二叉排序树的删除
🎱5.完整代码

我们可以看出:
- 只要左子树为空,就把小于父节点的数插入作为左子树
- 只要右子树为空,就把大于父节点的数插入作为右子树
- 如果不为空,就一直往下去搜索,直到找到合适的插入位置了解了如何构建后,我们不禁要问,这有啥用呀?感觉没啥特别的地方呢?别急!我们马上揭晓!
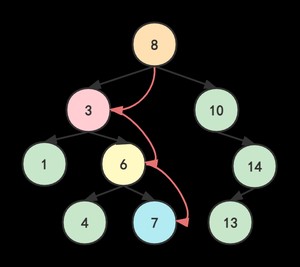
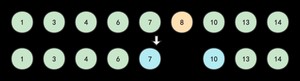
我们对这棵二叉树进行中序遍历,看看会发生什么?你自己试一试!
没错,这棵二叉树中序遍历结果为:
根据以上思路,我们其实就可以写出代码了,构建的过程其实就是插入的过程:
显然,它的效率会比在无序数组中挨着查找快多了吧!我们直接上代码。
那么删除就稍微比查找与插入复杂一点,因为需要分类讨论了。
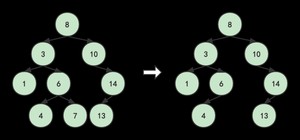
1.被删除结点为叶子结点
直接从二叉排序中删除即可,不会影响到其他结点。例如删去7:
那么删除就稍微比查找与插入复杂一点,因为需要分类讨论了。
1.被删除结点为叶子结点
直接从二叉排序中删除即可,不会影响到其他结点。例如删去7:
2.被删除结点D仅有一个孩子果只有左孩子,没有右孩子,那么只需要把要删除结点的左孩子连接到要删除结点的父亲结点,然后删除D结点;
- 如果只有右孩子,没有左孩子,那么只要将要删除结点D的右孩子连接到要删除结点D的父亲结点,然后删除D结点。
以D=14为例:它没有右孩子,只有左孩子。(先把10指向14的右指针移动,去指向13,然后再删除14)
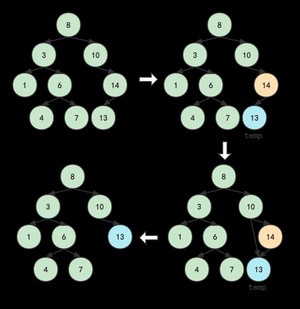
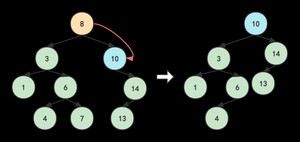
再以D=10为例,它没有左孩子,只有右孩子。(先把8指向10的右指针移动,去指向14,然后再删除10)
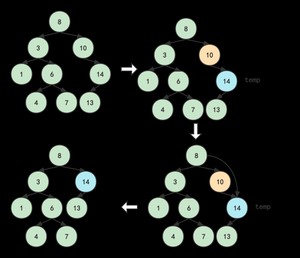
3.被删除结点左右孩子都在
这种情况就要复杂很多了。但没有关系,依然会讲的很清楚。
我们先假设删除根节点8,看看会发生什么?
我们的目标依然是要保证删除结点8后,再次中序遍历它,仍不改变其升序的排列方式。 那么我们只有用7或者10来替换8原来的位置。
我们先看7来顶替位置
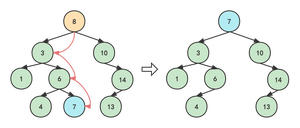
此时7从叶子结点“升迁”到了根节点(只是刚好要删除的结点为根节点,如果删除3,就替换3的位置)
我们再看10来顶替位置
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/2314.html