目录
转载请注明出处:bestsort.cn
树状数组基础
单点更新:
区间查询:
高级操作
求逆序对
操作
原理
求区间最大值
区间修改+单点查询
查询
修改
区间修改+区间查询
查询
修改
二维树状数组
单点修改+区间查询
区间修改 + 单点查询
区间修改 + 区间查询
树状数组是一个查询和修改复杂度都为log(n)的数据结构。主要用于数组的单点修改&&区间求和.
另外一个拥有类似功能的是线段树.
具体区别和联系如下:
1.两者在复杂度上同级, 但是树状数组的常数明显优于线段树, 其编程复杂度也远小于线段树.
2.树状数组的作用被线段树完全涵盖, 凡是可以使用树状数组解决的问题, 使用线段树一定可以解决, 但是线段树能够解决的问题树状数组未必能够解决.
3.树状数组的突出特点是其编程的极端简洁性, 使用lowbit技术可以在很短的几步操作中完成树状数组的核心操作,其代码效率远高于线段树。
上面出现了一个新名词:lowbit.其实lowbit(x)就是求x最低位的1;
下面加图进行解释
对于一般的二叉树,我们是这样画的
把位置稍微移动一下,便是树状数组的画法
重头戏来了,bestsort教你一图学会树状数组~(咱也不知道为啥其他博客写那么复杂
需要注意的是,图中的子节点包括自己,比如说8这个节点,里面的值是原始数组中[5,8]的和
标记为灰色的节点实际已被上层覆盖,不占据空间
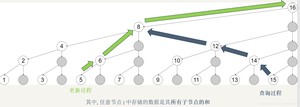
下面是二进制版本,能看到
更新过程是每次加了个二进制的低位1(101+1 ->110, 110 + 10 -> 1000, 1000 + 1000 -> 10000)
查询过程每次就是去掉了二进制中的低位1(1111 - 1 -> 1110, 1110 - 10 -> 1100, 1100 - 100 -> 1000)
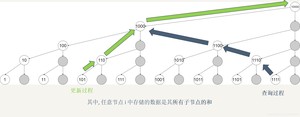
开篇就说了,lowbit(x)是取出x的最低位1;具体操作为
极致简短!!!!现在我们来理解一下这行代码:
我们知道,对于一个数的负数就等于对这个数取反+1
以二进制数11010为例:11010的补码为00101,加1后为00110,两者相与便是最低位的1
其实很好理解,补码和原码必然相反,所以原码有0的部位补码全是1,补码再+1之后由于进位那么最末尾的1和原码
最右边的1一定是同一个位置(当遇到第一个1的时候补码此位为0,由于前面会进一位,所以此位会变为1)
所以我们只需要进行a&(-a)就可以取出最低位的1了
会了lowbit,我们就可以进行区间查询和单点更新了!!!
--------------------------------------------------------------------------------------------
继续看开始给出的图
此时如果我们要更改A[1]
则有以下需要进行同步更新
1(001) C[1]+=A[1]
lowbit(1)=001 1+lowbit(1)=2(010) C[2]+=A[1]
lowbit(2)=010 2+lowbit(2)=4(100) C[4]+=A[1]
lowbit(4)=100 4+lowbit(4)=8(1000) C[8]+=A[1]
换成代码就是:
--------------------------------------------------------------------------------------------
举个例子 i=5
C[4]=A[1]+A[2]+A[3]+A[4];
C[5]=A[5];
可以推出: sum(i = 5) ==> C[4]+C[5];
序号写为二进制: sum(101)=C[(100)]+C[(101)];
第一次101,减去最低位的1就是100;
其实也就是单点更新的逆操作
代码如下:
lowbit会了,区间查询有了,单点更新也有了接下来该做题了
单击传送门移步HDU1166 敌兵布阵
附代码:
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/2261.html
