树壮数组



推荐在 cnblogs 阅读。

作为一个常数小且好写的数据结构，树状数组（Binary Indexed Tree，BIT）是求解数据结构问题的第一选择。

除了众所周知的区间加区间求和，树状数组还能代替常数巨大的线段树做很多事情，例如树状数组二分和维护高维差分。

很多选手对树状数组的了解仅停留在背诵层面，却不知道这短短的两行代码背后的实际含义。深入研究树状数组的结构有助于我们更好地理解和运用树状数组。

• 树状数组可以看做线段树的简化版本，这样的简化使得它只支持前缀（或后缀）查询。因此，用树状数组维护的信息一般需要具有可减性。若信息没有可减性，则要求查询前后缀，或转化为查询前后缀。

考虑最基本的问题：单点加，单点求前缀和。设序列为 。

树状数组的核心思想在于，将一次前缀查询 拆成对 个子区间求和，使得对于所有 ，不同的子区间的总数为 。有的读者会指出：这不是和线段树一个道理吗？没错，但是树状数组做到了不同的子区间的总数恰好为 。

对于任意正整数 ，我们都可以将其拆分为 个 的幂，例如 。

同样的，对于区间 ，我们可以拆成 个子区间，满足每个子区间的长度为 的幂。

考虑 在二进制表示下每一个为 的位 ，设 且 ，我们将 拆分为 。例如，对于 ，将 拆为 。

这样拆分有一个非常好的性质：对于每个右端点 （），在所有不同的子区间中，与之对应的左端点 是唯一的。这是因为，假设存在子区间 ，根据我们的拆分规则， 一定由 加上某个 的幂得到，且一定是 在二进制表示下最低位的 对应的 的幂 （这就是 的定义），记作 ，以下简记为 。因此，。

这说明不同的子区间总数 恰好为 ，同时给予我们方便地维护子区间信息的方式：记录在右端点上。也就是说，用一个长度为 的数组 维护每个子区间的和，其中 表示子区间 的和，即 。

对于查询 ，从 出发不断令 减去 直到 ，经过的所有状态的 值之和即为所求。

接下来一大篇全部是关于修改的。

分析所有包含 的区间的形态。设区间 包含 （），称为 是 的祖先。

考虑 和 在二进制下从高到低第一个不同的位置 。除去 的情况， 一定存在。又因为 ，所以 的第 位为 ， 的第 位 。如果 在低 位（第 位）还有 ，那么 的第 位仍为 ，和 矛盾。因此， 的低 位全部为 ，则 的低 位为 。此时若 在低 位还有 ，则符合 的条件，否则 ，不符合条件。

这是合法的例子（）：

这是不合法的例子：

第一个例子因为 在低 位还有 ，所以 的第 位为 ，；第二个例子因为 在低 位没有 ，所以 。

根据条件，我们可以直接构造所有 的祖先 ：考虑 的某个 位，且存在 位低于该位，将该位变成 ，其低位全部变成 ，就是一个合法的 。相当于直接枚举 。

例如，对于 ，所有合法的 形如（）：

可以很明显地看出，对于 ， 是 的祖先，且相邻的 之间存在递推关系：。两个结论的证明留给读者自行思考。

我们令 表示 的 父节点编号，得到一个树状结构，则 的所有祖先就是 。也就是说，该结构完整地描述了每个位置的所有祖先，如下图（图源）：

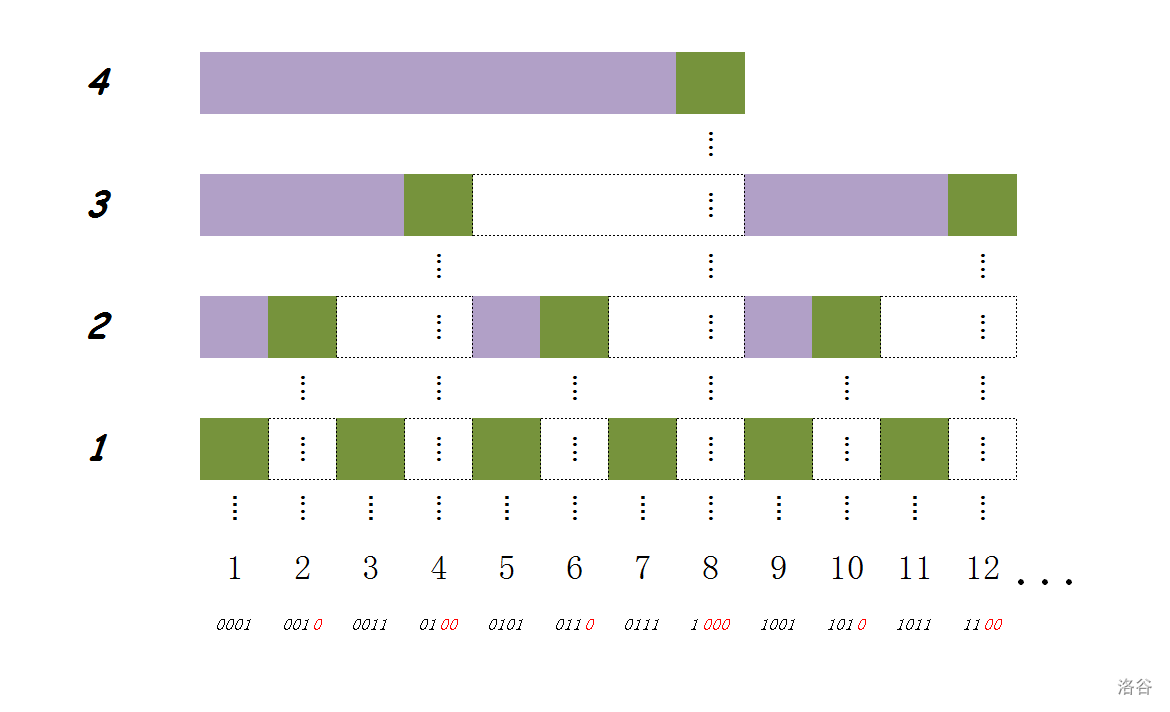
综上，对于修改 ，从 出发不断令 加上 ，更新经过的所有状态即可。

将修改和查询放在一起看，再来一张图加深印象（图源）：

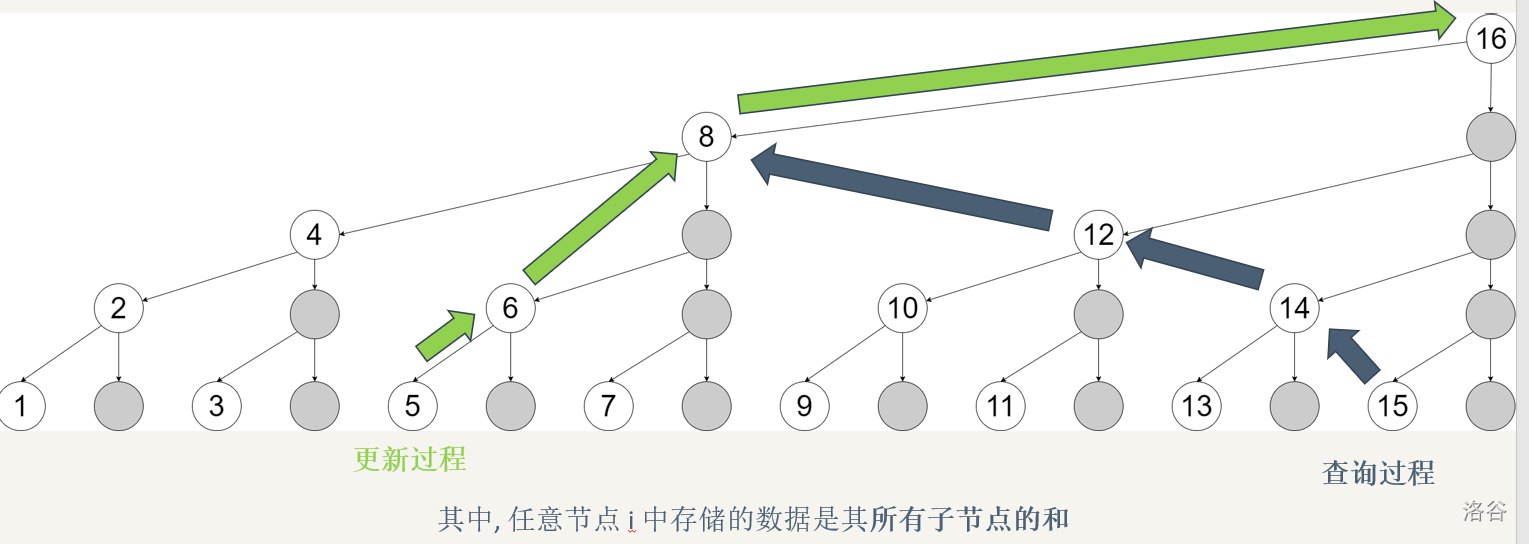
实际上，我们可以将树状数组看成 省略了所有右儿子的线段树。

从另一种角度也可以推导出上述结果：尝试证明所有区间包含或相离。满足条件的区间集合可以建树，求出每个区间的父亲，即包含该区间的长度最小的区间对应右端点编号。具体细节留给感兴趣的读者自行补充。

怎么算呢，总不能再 枚举吧！

用预处理 确实可行，但这样不仅没有技术含量，而且会增大内存访问次数，有愧于树状数组小常数的名号。

计算机用补码存储和表示数值。考虑 （）的补码，它等于 的反码 。设 ，我们发现 的补码在低 位（第 位）都是 ；在第 位和 相同，均为 ；在高于 的位和 相反。

例如，对于二进制数 ，其 值为 ，其反码为 ，相反数的补码为 。又因为正数的补码就是它本身，所以一个数的 值就等于它和它的相反数的按位与，即 。

这样，我们可以顺利成章地写出支持 模板题 操作的树状数组了。

类似线段树二分，树状数组也可以二分。只要理解了树状数组的结构，就很容易理解树状数组二分。

它可以抽象成这样一类问题：存在分割点 ，使得 的位置满足某个限制，而 的位置不满足该限制，求 。注意，树状数组二分是 在整个序列上二分，它不支持从某个位置开始二分，必须将后者转化为前者。

考虑查询最后一个前缀和 的位置，满足序列每个元素非负，则存在分割点 ，使得 的位置的前缀和 ， 的位置的前缀和 ， 即为所求。

树状数组二分的本质是 倍增。设当前位置为 ，对应前缀和为 。从大到小枚举 ，尝试将 加上 ，即检查 是否不大于 。因为 是从大到小枚举的，所以此时 ，因此 ，这说明 。因此，若 且 ，则令 ，再令 ，否则 超出下标范围或 ，不进行任何操作。

最终 一定等于 ，否则过程中 一定会变得更大。

P6619 [省选联考 2020 A/B 卷] 冰火战士

太经典了。

首先将温度离散化，就是求冰系战士能力关于温度的前缀和，与火系战士能力的后缀和在某个温度处较小值的最大值。由于能力都是正整数，所以前缀和单调递增，后缀和单调递减，考虑用树状数组维护冰火战士能力关于温度的前缀和（后缀和等于总和减去前缀和）。

每次查询二分找到最大的 使得 ，以及最大的 使得 且 最小，两者对比取更优解即可。但是满足条件的 是一段后缀（树状数组二分要求满足条件的位置是一段前缀）怎么办？将 平移一位变成 ，求出 之后相当于找最大的 使得 ，这样满足条件的 就是一段前缀了。

时间复杂度 。代码（UOJ 最优解）和 卡常后的代码（UOJ 更优解 & 洛谷最优解 2023.4.7，看看你能不能读懂）。

P4602 [CTSC2018] 混合果汁

整体二分，则问题相当于将所有美味度不小于当前二分值的果汁拎出来，按单价从小到大排序，求买 升的价格。用 BIT 维护每个单价的果汁体积，可以二分出最大单价 使得单价不大于 的果汁体积 小于 ，则买单价不大于 的果汁和 升单价为 的果汁即可（单价为 的果汁一定至少有 升，否则 还可以更大），注意需要先比较一下 和果汁总体积。

注意在每次 之前，需要保证所有美味度小于 的果汁已经加入 BIT，才能保证整体二分的时间复杂度仅与当前二分区间长度相关。

使用 BIT 倍增，时间复杂度 。代码。

P3586 [POI2015] LOG

每次贪心选最大的 个肯定没问题，但没办法直接模拟。

每个数之间顺序无关，一般通过排序寻找性质：对于最大的元素 ，若 说明 必定能贡献 次取数，令 ，考虑剩下来 个数，这是子问题。递归边界是出现 ，这说明 都小于 。问题转化为要求选 次，每次选 （这里的 实际上是询问的 减去 的数的个数）个不同的数，每个数被选择的次数不超过 ，其中 。

证明：看成一个 的表格（左上角标号 ，右下角标号 ），每一行的数互不相同且 的出现次数不超过 ，有如下构造：对于每个 ，有 次填数，每次选择最左边有空位的列的最上面那个位置填入 即可，即填数的轨迹是这样的：。因为轨迹上任意连续 个格子横坐标互不相同，所以满足限制。

判断是否有 即可。具体地，求出 的 的个数 ，以及所有小于 的数的和 ，若 则可行，否则不可行。离散化 + 树状数组二分即可。

时间复杂度 。代码（洛谷最优解 2023.4.8）。

[模拟赛] 集合

维护初始为空的序列 ，支持插入一个数或询问 ，求出最多进行多少次选出 个数并减去 。

，。2s，512MB。

和上一题（P3586）思想差不多，但是稍微难一点。

考虑哪些元素每次必然被选，自然从最大值开始考虑。设最大值为 ，总和为 ，则最多选择 （所有分数下取整）次。若 ，说明 每次必然被选，令 并丢掉 ；若 ，就是上一题的结论，可以选满 次。

将所有数从大到小排序，相当于找到最后一个位置使得 ， 表示后缀和。感性理解，满足条件的位置一定是一段前缀（不存在 使得 每次都被选择了且存在一次没选择 ，否则可以调整）。

证明：变形得 ，即 ，即 。注意到 在 增加 时，值最多减小 （），所以不等号右侧非严格递增。

离散化 + BIT 二分找到最后一个满足条件的位置，则 即为所求。

时间复杂度 。

上面讨论的都是前缀 BIT，前缀表示查询一段前缀。它本质上是 一阶前缀和：在 处的修改对所有 处的查询产生贡献。

对于单点加区间求和，转化为 “单点修改原序列” 对 “某个位置的前缀和” 的贡献：给 加上 相当于给 （）加上 ，即位置 的加 的修改会让所有位置 处的查询加上 。

对于区间加单点查询，转化为 “单点修改差分序列” 对 “原序列的某个位置” 的贡献：给 加上 相当于给 （）加上 ，原理是类似的。

当问题来到高阶前缀和，应当如何去思考？简单，只需要梳理清楚某处修改对某处查询的贡献即可。

对于区间加区间求和，转化为 “单点修改差分序列” 对 “某个位置的前缀和” 的贡献。这是二阶前缀和。

考虑给 加上 ，在 处查询前缀和 。 加了 使得 全部加了 ，所以 加了 。将贡献拆成 和 。我们用两个树状数组 ，分别维护修改值 的一阶前缀和，和修改值 乘以修改位置 的一阶前缀和，那么 处的二阶前缀和就等于修改值在 处的一阶前缀和乘以 ，减去修改值乘以修改位置在 处的一阶前缀和。

换言之，我们考虑 单次修改对单次查询的贡献。对于某种维护方式，只要单次修改对单次查询的答案是对的，那么无论多少次修改，多少次查询，它依然正确。

支持线段树 模板题 操作（区间加，区间求和）的树状数组如下：

对于更高阶前缀和，思路是一致的。

假设 ，用矩阵（行列均从 开始标号）的第 行表示 阶前缀和从 到 的贡献系数序列，则

对组合数较熟悉的同学已经发现，矩阵第 行第 列就是 。推导过程不难，归纳即可。

综上，对于 阶前缀和， 处加 对 处的查询产生的贡献为 。理解方式：考虑贡献路径 ，每一个这样的 都对应 的贡献。换言之，建出这样一张图：对于任意 ， 向 连边，从 恰好走 步到 的方案数就是贡献系数。这是经典问题，相当于在 个空隙放入 个插板，两个插板可以放在不同的空隙；也相当于将 个球装入 个不同的盒子，可以有盒子为空。有方案数 。

为定值， 是关于 和 的多项式。对于所有含 的项，将 提出得到关于 的多项式，设为 。维护所有 （）的 一阶 前缀和，查询时算出 在 处的前缀和 ，则 即为所求。

例如，当 时，。提出 ，展开得到 ，即 。因此：

• 求出 即 在 处的前缀和，乘以 。
• 求出 在 处的前缀和，乘以 。
• 求出 在 处的前缀和，乘以 。

将上述三个结果相加即为所求。

时间复杂度 ，其中 表示前缀和阶数， 表示操作次数， 表示序列长度。

本质上是树状数组套树状数组，用二维数组维护。它可以直接做单点加矩形查询，且矩形两维的左边界都是 。差分一下就可以对任意矩形求和。

对于矩形加矩形求和，即维护二维差分数组的二阶二维前缀和。类似地，考虑 处对二维差分数组的修改对 处查询二维前缀和的贡献。给 加 使得 全部加了 ，所以 加了 。拆开变成 。用四个树状数组分别维护 ，， 和 的一阶二维前缀和即可。

时间复杂度 。

模板题 代码：

交换查询和修改的跳转方式就是后缀 BIT 了。

可以这样思考：在前缀 BIT 中，对于 ，一个 处的更新对 处的查询产生了贡献。类似地，在后缀 BIT 中，一个 处的更新对 处的查询产生了贡献。

不断增大的操作只会影响所有位置不小于 的信息（或和这样的信息有关）， 不断减小的操作只会影响所有位置不大于 的信息（或和这样的信息有关）。

对于可减信息，用前缀后缀 BIT 维护是一样的。后缀 BIT 的用途在于，当信息不可减且询问具有良好性质（询问后缀，或可以转化为询问后缀）时，能够不翻转序列地维护修改和查询，避免因翻转序列产生的大量下标变换使得代码写挂。

第一章

• 补码 —— 百度百科。

版权声明：

本文来源网络，所有图片文章版权属于原作者，如有侵权，联系删除。

本文网址：https://www.mushiming.com/mjsbk/2176.html