本文课件来自香港科技大学，我的母校，感谢ELEC
本节介绍RRT/RRT*的算法：
RRT的基本原理是：
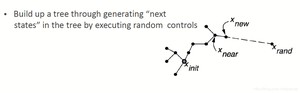
我们首先初始化我们的起点，接下来随机撒点，选出一个x_rand, 在x_near 和 x_rand之间选择一个x_new, 再在原有的已经存在的x中找到离这个点最近的点将这两个点连接起来，同时这个最近的点也会作为x_new的父节点。
RRT算法的伪代码如下：
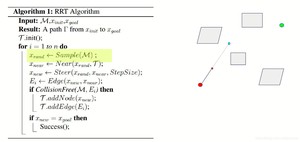
对照着图，再看一次：
首先我们随机生成一个点，x_rand
然后再tree上面找到最近点，作为x_near
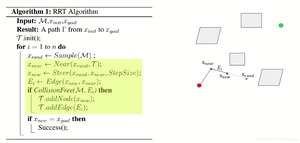
然后取两者中间的点作为x_new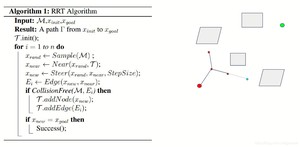
最后，还要做一次collision checking, 看看生成的点是不是和x_near 连接起来后会碰撞障碍物：
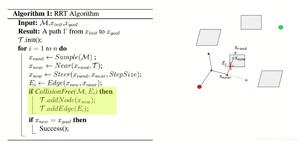
按照这个方法一直搜索，一直打到停止搜索的标准，比如x_new与终点的距离小于某个极小的epsilon。另外一个，在搜索最近的x_near的时候，我们可以使用KD tree来加速搜索：
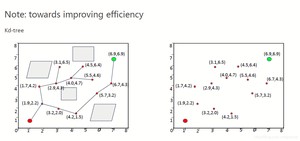
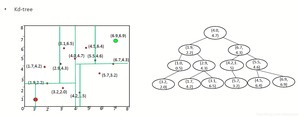
具体看一下(https://blog.csdn.net/junshen1314/article/details/)
接下来我们分析一下RRT的优缺点：
RRT比概率图方法更加有效，但是这依然不是个高效的搜索方法，并且获得的解也不是最优解。
接下里，我们有一些对RRT的优化方法：
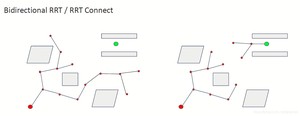
第一种方法就是双向RRT， 意思就是从起点和终点同时搜索，一直到两棵树交汇
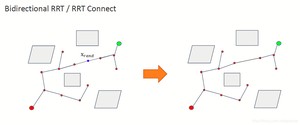
下图中可以看到，起点和终点同时生成树进行搜索。
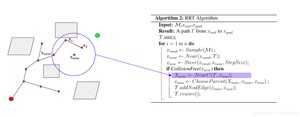
第二种方法我们介绍RRT*
伪代码流程如下：
这个算法是在RRT基础上的改进，改进的地方是这个x_near 和 x_new不会直接连接起来，而是做一个优化处理，方式就是：
我们在x_near附近圈一个圆，将被圈在圈内的各个点与x_new的距离作对比：
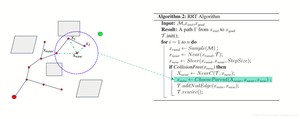
如果x_near 到 x_new的距离比通过x1,x2后再到x_new的距离低，就将x_near和x_new连接起来。
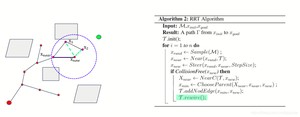
同时我们还要对比，从x_near出发，到x2的距离最短值：
我们发现通过x_new之后到达x2的距离更短，所以就将x2的父节点更新为x_new. 这个步骤我们称之为rewire function.
当然我们还有其他的优化，包括考虑动力学限制的优化：
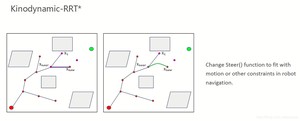
接下来我们提供一系列源代码供读者进行测试：
首先提供2D RRT
另外请调用函数：
还需要图片：
把这个图片保存在运行目录下。
最后运行的效果是这样的：
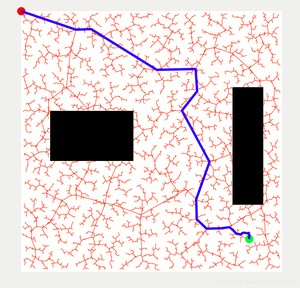Matlab社区中，我们也找到了参考的代码，RRT* 2D/3D
其中调用函数：
运行效果是这样的：
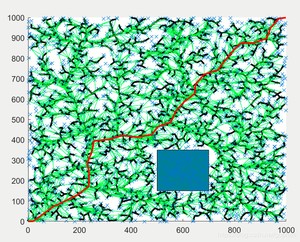
RRT* 3D
调用的函数是：
运行的结果是：
版权声明：
本文来源网络，所有图片文章版权属于原作者，如有侵权，联系删除。
本文网址：https://www.mushiming.com/mjsbk/1838.html