归并排序c++代码



归并排序（Merge Sort）

在排序算法的历史上，归并排序是第一个可以在最坏情况依然保持的运行时间的确定性排序算法，由冯诺依曼与1945年在EDVAC上首次编程实现。

归并排序的思路简单，速度仅次于快速排序，为稳定排序算法。一般用于对总体无序，但是各子项相对有序的数列。在模式上有：分（Divide）、治（Conquer）、合（Combine）三个步骤，主要有迭代法和递归法两种实现方法。适用于数组基本有序、外排序等情况。

本文主要以递归法对归并排序流程进行讨论、实现和分析改进。

策略：分而治之（divide and conquer）

• 以上递推和回归的二叉树高度均为为

按照以上流程可以先将列出解题框架，显然用递归是可以实现的。列框架可大致分为3步：

1. 分：将一个数组分为若干个子数组
2. 治：将分解好的子数组两两排序（这里可以将看做：大数组=左数组+右数组），排序算法要考虑一般情况。（sort）
3. 合：将排好序的代码合并。（merge）

按照上述思路先列出框架，由于在合并时需要排好序，所以治、合步骤需要在一个函数中实现，即：

细节设计

①分：以数组中间为分界线，分为左数组和右数组。即左数组和右数组分别调用mergeSort()，重复该过程一直到达递归基。
代码块

②治、③合：
（封装在merge函数中）
这里的实现方法有很多个版本，仅选用个人认为可读性最好的一种解释。

考察最一般的情况：在mergeSort()递推完毕，回归未结束程序时，此时左右数组在程序中是分区间标记的。此时在原区间上是无法排序的，就需要开辟一块新的内存空间，此时需要左右数组的指针和新开辟空间的指针，方便维护。
所需创建的变量和向量前后的哨兵如图：

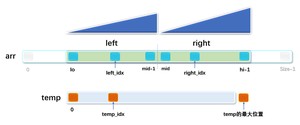
对应代码块：

由于自递归深入点（最内层），每一步都会执行一次merge操作，故在使用merge合并数组后就会使得相对外部的一层left和right成为有序序列，下一步要做的就是实现此操作。
设有序向量：{1,3,7,9} 和 {2,4,6,8}，观察下图合并过程：
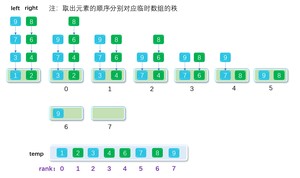每次移动赋值一个元素，temp_idx都会对应向后移动一个单元，直到right和left未经比较的元素耗尽（可作为循环终止条件）。而针对left和right指针同理，每次在绿色框（针对当前的arr[left_idx]和arr[right_idx]两个元素）内比较后，拿出较小的一个数即可，对应的left_idx或right_idx++.

注：若排序方向从小到大，则将代码块中的if条件改为arr[left_idx] < arr[right_idx] 即可，一步到位。因为这里隐含条件是：其中left和right之一耗尽后，剩余的元素都是较小的。

对应代码块：

如果细心一些就会发现，如果left或right之一元素已经耗尽，存在 left_idx < mid 和 right_idx < lo 两种情况，那么这些数就是比较大的数，直接复制到temp即可。

代码块：

注意：一般情况和数组元素耗尽的情况处理是需要有顺序的，应先处理一般情况，再处理left和right耗尽的情况，否则left和right会直接分别复制到temp中去，使得排序失败。
left和right耗尽的两种情况出现顺序无要求。

ok，经过一顿操作后temp就是有序的了，最后temp中的数据复制到arr中的对应位置 [lo,hi) 之间，将临时数组temp释放就完成了。

③合：

• 以上代码算法是不稳定的.
• 更简洁的实现方法可参考邓公的《数据结构C++》P63页代码2.29.

运行结果：

整合代码：

将情况③while中的if条件判断改为 arr[left_idx] > arr[right_idx] 之后的运行结果（此时归并时右侧元素优先归为合并至左侧，即满足A[i] > A[j] ，且i > j，算法稳定）：

先复习一下稳定性的定义：

若对于向量A中每一对重复元素 A[i] = A[j] （相应的S[ki] = S[kj]），都有i < j 当且仅当 ki < kj ，则称为该算法是稳定算法（stable algorithm）。

本文后面改进的代码会使用稳定的算法.

改进点1：

注意到在进入归并函数merge时都要申请一部分空间。这里根据而反复通过new和delete操作申请和释放辅助空间。从实验统计表明，这类操作的实际时间成本大约是常规运算的100倍，故往往成为制约效率提高的瓶颈.

不难想到，我们可以统一申请一块缓冲空间解决空间增长速度过大的问题。即在全局区申请一块足够大的辅助空间（与arr的大小向同即可），其大小可用一个“指针”temp_idx维护，即每次调用merge时可以将temp_idx归零.

• 优势：可以将动态申请的次数降至O(1)，而不再与递归示例的总数O(n)相关。在全局区可以分配给变量的内存空间更大。
• 劣势：会在一定程度上降低代码的规范性和简洁性，代码调试的难度也会有所增加。

改进点2：

我们还可以进一步降低时间成本，可考虑较好的情况：有一段子序列已经排好序。此时我们就没有必要再调用merge算法对其再排序。相应的只需要增加线性时间：
对于规模为n的向量，扫描一遍共增加 =
不影响总体时间复杂度.

按照算法流程，在二路归并前，将arr[mid-1]：左侧区间的末元素 与arr[mid]右侧区间的第一个元素比较。若整体有序，则必有 arr[mid-1] ≤ arr[mid]，故可判断并省去merge操作.

此方法即在merge(arr, lo, mid, hi); 前加 if (arr[mid - 1] > arr[mid]) 即可.

改进后代码（稳定）：

注意：若降序排列在上文的基础之上需要将改进点2处对偶地改为：

才能在此基础上保证算法的正确性、稳定性，分析方法同上文。

时间复杂度：

使用递归方程分析法，对长度为n的向量进行归并排序，需递归地对长度为n/2d1两个字向量做归并排序，再花线性时间做一次合并，有以下关系：

第二个式子两边同除n得

令
有：

即有

空间复杂度：

二叉树的高度为logn，将临时数组temp压入栈的数据占用的空间为n，故将，所以空间复杂度为 ：O(logn+n) =

参考资料

《数据结构C++语言版》（第三版）邓俊辉编著

从学完MergeSort后独立写了第四遍才运行成功（还是我太菜了），没有写成功的原因：

1.将sort部分和merge部分混起来写，致使每一个功能模块混淆
2.没有列框架，思路不够清晰
3.变量名的可读性差，不利于理顺思路

本文尽可能细化到代码的每一个细节，并使用较多的注释，方便日后以最快的时间回顾，并帮助彻底理解和掌握mergeSort.

限于本人处于数据结构初学阶段，若本文有疏漏之处，欢迎批评指正。

版权声明：

本文来源网络，所有图片文章版权属于原作者，如有侵权，联系删除。

本文网址：https://www.mushiming.com/mjsbk/1776.html