「前言」
🌈个人主页: 代码探秘者
🌈C语言专栏:C语言
🌈C++专栏: C++ / STL使用以及模拟实现
🌈数据结构专栏: 数据结构 / 十大排序算法
🌈Linux专栏: Linux系统编程 / Linux网络编程(准备更新)
🌈喜欢的诗句:天行健,君子以自强不息.

二叉树的遍历是指按某条搜索路径访问树中的每个结点,使得每个结点均被访问一次,而且仅能访问一次(说明不可二次访问,一遍而过)。
- 遍历一颗二叉树便要决定对根结点N、左子树L和右子树的访问顺序。
- 二叉树常的的遍历方法有=前序遍历、中序遍历和后序遍历三种遍历算法,三种遍历方法有递归和非递归两个版本。
- 当然还有层序遍历
力扣链接:二叉树前序遍历
i、先访问根结点;
ii、再前序遍历左子树;
iii、最后前序遍历右子树;
简单版本的实现:
前序遍历的非递归算法,即利用一个栈,来进行访问结点并入栈遍历左子树,结点出栈遍历右子树。
1. 思路
算法思路:
1、二叉树为空啥也不做;
2、结点不为空,访问(把遍历结果保存)并入栈,,遍历其左子树;
3、栈顶元素出栈,遍历栈顶元素的右子树(循环又回来,如果它还有左子树,继续入完);
4、结点为空并且栈为空结束遍历。
2. 图解
图解前序遍历的递归算法:
咱们看下面的二叉树是怎样利用递归函数实现前序遍历:
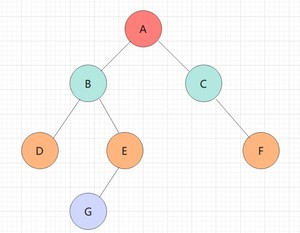
📖入栈步骤核心:
先访问,再入栈,如果访问节点的左子树不为空,再继续访问(左子树的左子树…),一直入完左路节点为止,才能开始出栈
不为空树,cur != nullptr,访问(把遍历结果保存)A,并入栈A
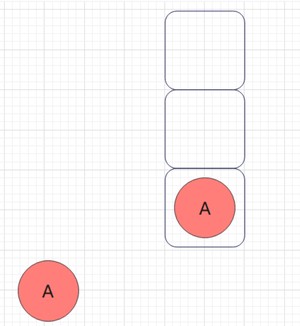
A的左子树不为空,遍历B,并将B入栈,遍历B的左子树:
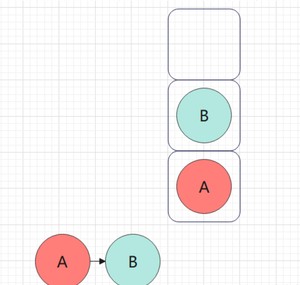
B的左子树不为空,遍历D,并将D入栈,遍历D的左子树:
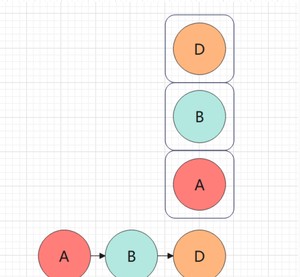
下面可以看到,D无左子树,其本身都遍历完。
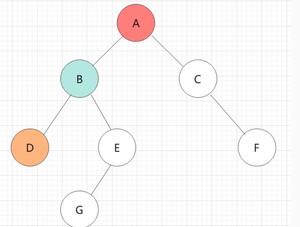
📖出栈步骤核心:
先取栈顶元素出栈,如果出栈元素的右子树不为空,要访问继续访问它的右子树,进入下一轮循环(先访问它右子树的左子树…)

先出D,访问右子树,但是显然没有右子树
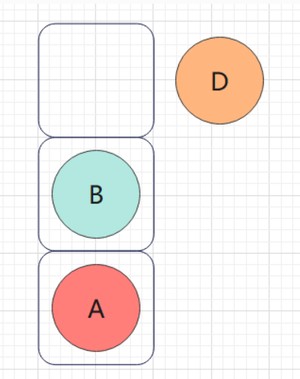
然后B出栈,遍历B的右子树E
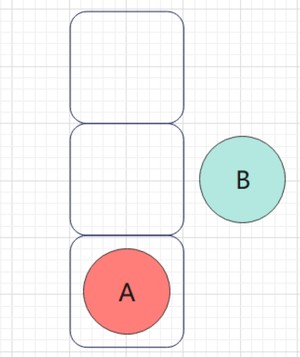
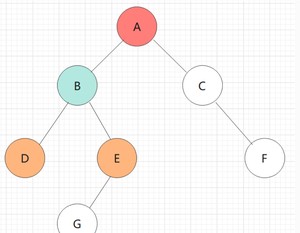
访问E,入栈
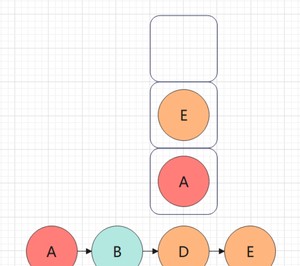
E的左子树不为空,遍历G,G入栈,遍历G的左子树(显然为空,右子树也为空)
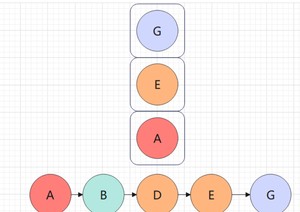
G的左子树为空,不遍历,G出栈遍历G的右子树,但G的右子树为空,故也不进行遍历:
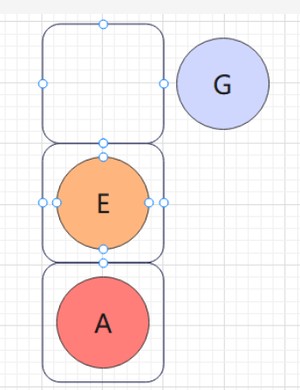
此时,栈中有E、A结点,E出栈,遍历E的右子树,但E的右子树为空,故不进行遍历:
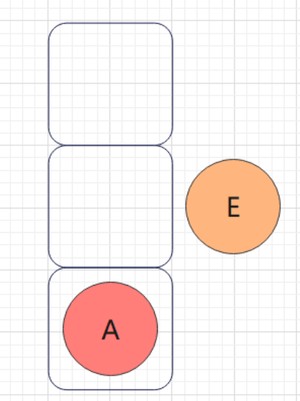
然后A出栈,A的右子树不为空,遍历A的右子树:
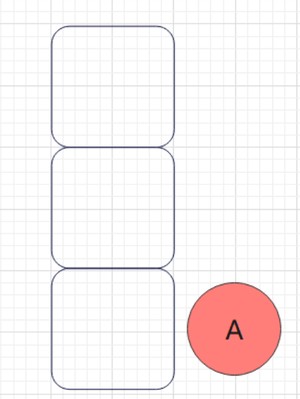
遍历C,C入栈,遍历C的左子树:
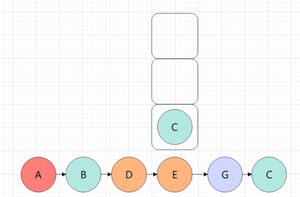
C的左子树为空,不遍历,C出栈,遍历C的右子树:
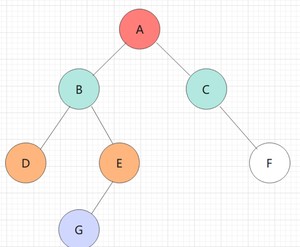
遍历F,F入栈,遍历F的左子树:
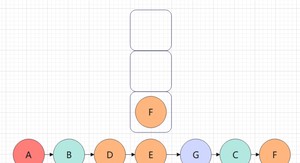
F的左子树为空,不遍历,F出栈,遍历F的右子树:
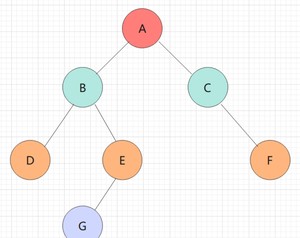
F的右子树为空,不遍历,此时栈为空,结束遍历,二叉树的全部结点有且仅有一次被访问:
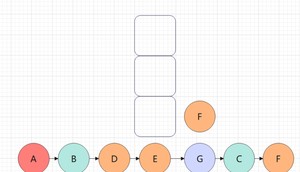
前序遍历的结果为:

3. 代码
算法实现:
力扣链接:二叉树中序遍历
i、中序遍历左子树;
ii、访问根结点;
iii、中序遍历右子树
简单版本的实现:
1.思路
中序遍历的非递归算法,就是将上面递归函数隐式调用栈的过程给显示表示出来,即利用一个辅助栈,来进行结点入栈访问结点的左子树,出栈访问结点,并且遍历结点的右子树。
算法思路:
1、二叉树为空,啥也不做
2、结点不为空,入栈,并遍历其左子树
3、结点的左子树为空但栈不为空,栈顶元素出栈并访问,接着遍历栈顶元素的右子树;
4、栈为空,且结点也为空结束遍历。
2.代码
下面是前序非递归的代码
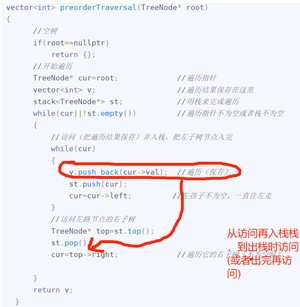
这里是中序非递归的代码,其实没变化什么,就访问时间发生变化
力扣连接:二叉树的后序遍历
算法思路:
若二叉树为空,什么也不做,否则:
i、后序遍历左子树
ii、后序遍历右子树
iii、访问根结点
算法实现:
1. 思路
- 当二叉树为空,则什么也不做;
- 结点不为空,先入左路节点
- prev:记录访问的上一个节点
- 出栈条件:右子树为空或者top->right=prev(说明右子树已经访问完)
- 如果右子树不为空,top->right!=prev(右子树没有访问完),得访问其右子树,不能出栈
- 出栈+访问,更新prev(记录访问的上一个节点)
2. 图解
为了简单了解思想,我这里演示遍历这个树(这里只有树的一半,不过已经够了哦)
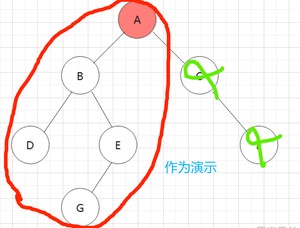
📖 tip1
- 先入左路节点
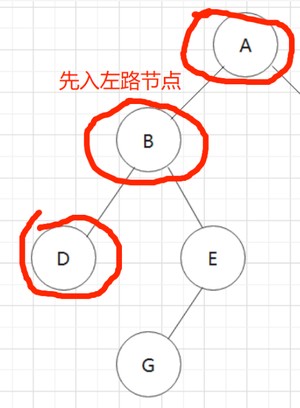
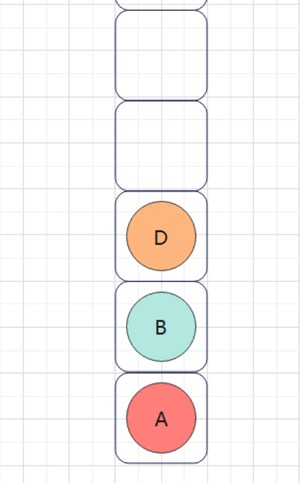
📖 tip2
- 这里重要细节,我用一个prev指针保存前一个访问的节点
开始出栈:D没有左右节点,直接出,遍历
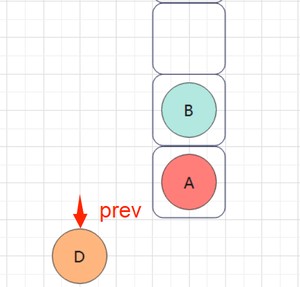
📖 tip3
这里B不能直接出,为什么?
- 得访问B的右路节点,所以得继续入栈.
B什么时候能出?
- top->right=prev(核心)
- 就是E出了下一个B才能出哦
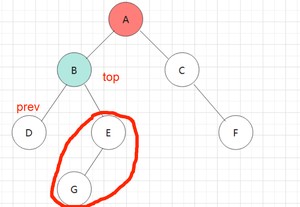
下面分别入E、以及它的左路节点G。
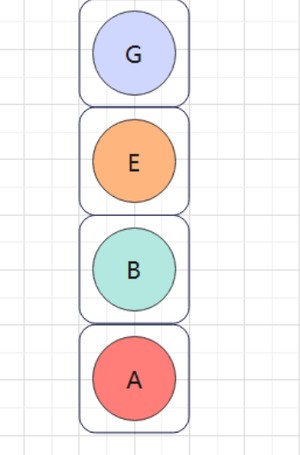
出G
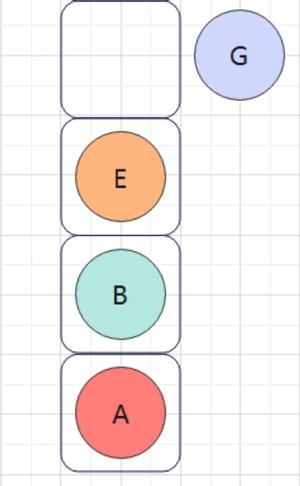
📖 tip4 - 访问节点,记得更新prev(上个一个访问的结点)
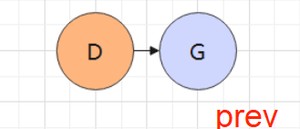
出E
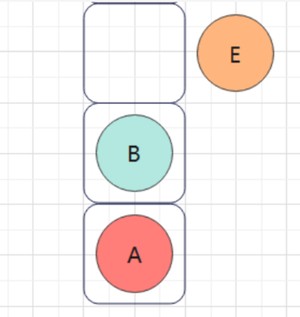
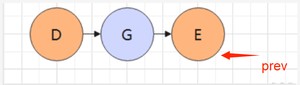
📖 tip5
- 这里B可以出栈,因为top->right=prev
- 这是后序非递归区别前中序的非递归的核心步骤
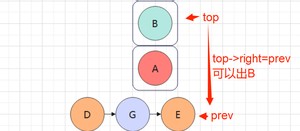
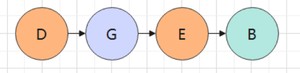
A再出栈
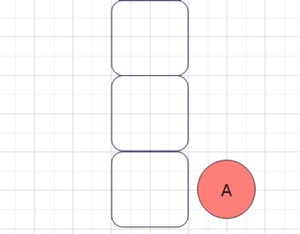
完成遍历(这里我值演示了遍历整个树的左子树)
遍历结果:D->G->E->B->A
3. 代码
运行结果:
1. 思路
顾名思义,对于树型结构,层序遍历就是按层从上到下,每层按一定顺序对树的节点进行遍历。我们通过如图所示的二叉树进行说明:对于左边的二叉树,按层划分后可得到右边的分层结构。
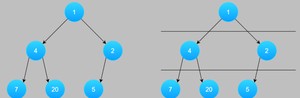
这个树层序结果就是:1 4 2 7 20 5
2. 图解
- 创建一个队列(根节点入队)
- 取队头元素,出队
- 如果队头元素有左、右孩子,就依次入队
- 队列为空,遍历结束
先入根结点
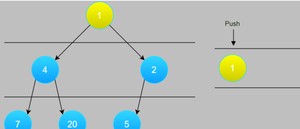
删1,把左右孩子4,2 带进来
此时遍历结果为:1
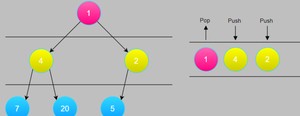
删4,把左右孩子7,20 带进来
此时遍历结果为:1 4
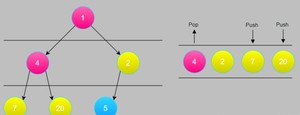
删2,把左孩子5 带进来
此时遍历结果为:1 4 2
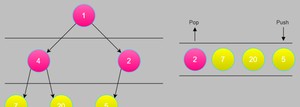
之后依次删吧



队列为空,遍历完成!
此时遍历结果为:1 4 2 7 20 5
3. 代码
4. 力扣:层序遍历
要求把遍历结果放二维数组返回,每行就是每层遍历的结果
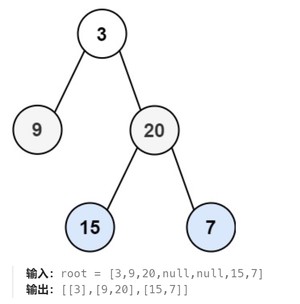
5. 力扣:锯齿形层次遍历
力扣链接
- 即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行
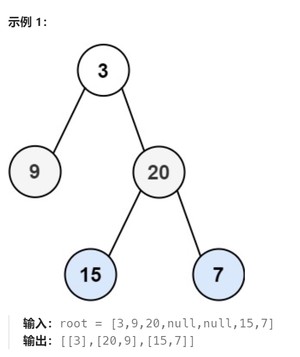
在原来层序遍历的基础上,加间隔一层反转
思路:
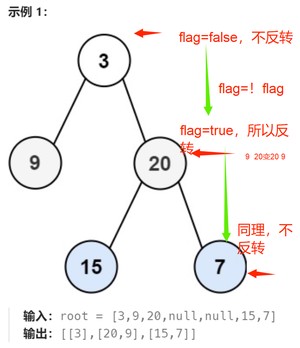
代码
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/14790.html
