二叉排序树的构造方法



二叉排序树或者是一棵空树；或者是具有如下特性的二叉树：
若它的左子树不空，则左子树上所有结点的值均小于根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于根结点的值；
它的左、右子树也都分别是二叉排序树。
(左小右大)

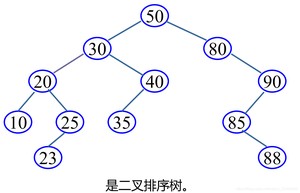
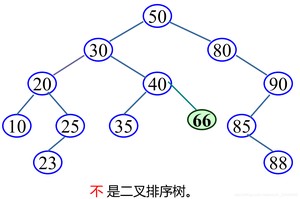
通常，取二叉链表作为二叉排序树的存储结构

1. 若给定值等于根节点的关键字，则查找成功
2. 若给定值小于根节点的关键字，则继续在左子树进行查找
3. 若给定值大于根节点的关键字，则继续在右子树上进行查找

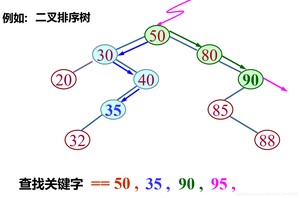
从上述查找过程可见
在查找过程中，生成了一条查找路径：

从根节点出发，沿着左分支或右分支逐层向下直至关键字等于给定值的结点——查找成功

从根节点出发，沿着左分支或右分支逐层向下直至指针指向空树为止——查找不成功

根据动态查找表的定义，“插入”操作在查找不成功时才进行;

若二叉排序树为空树，则新插入的结点为新的根结点；否则，新插入的结点必为一个新的叶子结点，其插入位置由查找过程得到。

例如

从空树出发，经过一系列的查找、插入操作之后，可生成一颗二叉排序树

{10，18，3，8，12，2，7}

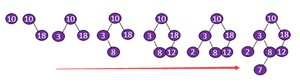
不同插入次序的序列生成不同形态的二叉排序树

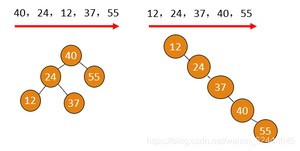
结论

• 一个无序序列可以通过构造一棵二叉排序树而变成一个有序序列
• 每次插入的新节点都是二叉排序树上新的叶子节点
• 插入时不必移动其他结点，仅需修改某个结点的指针
• 中序遍历二叉排序树可以得到一个关键字的有序序列

• 被删除的结点是叶子
• 被删除的结点只有左子树或者只有右子树
• 被删除的结点既有左子树，也有右子树

(1)被删除的时叶子结点

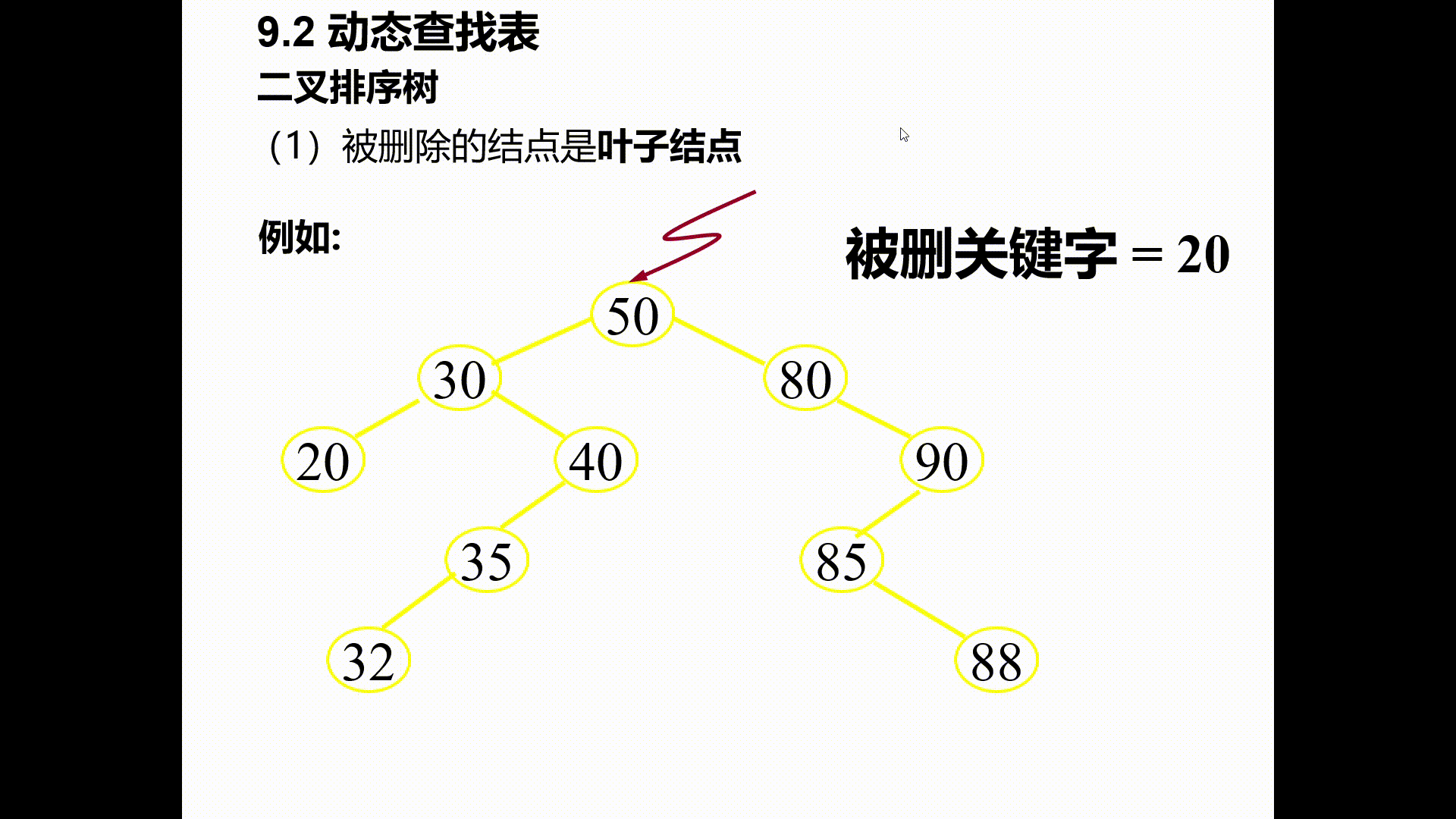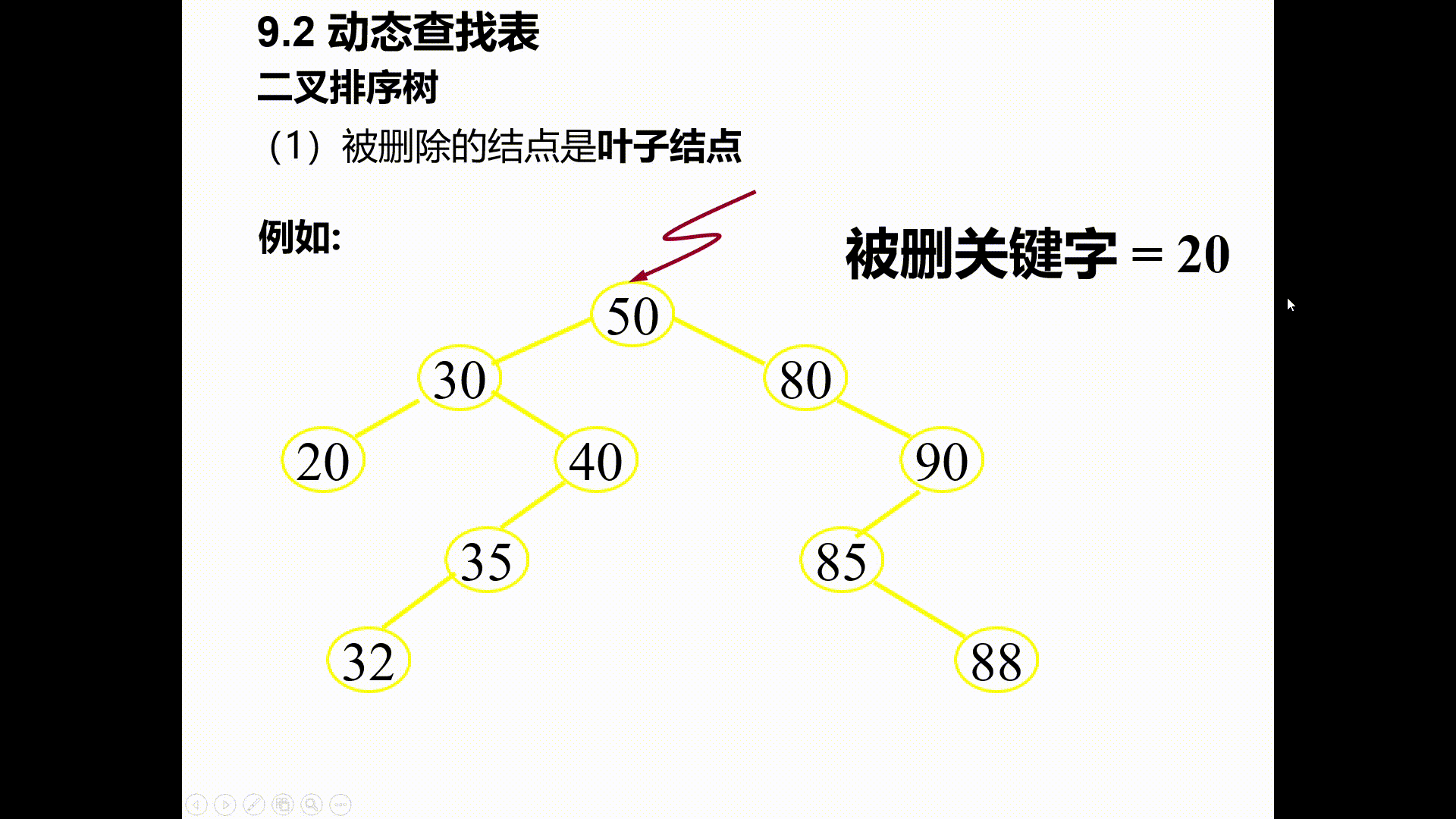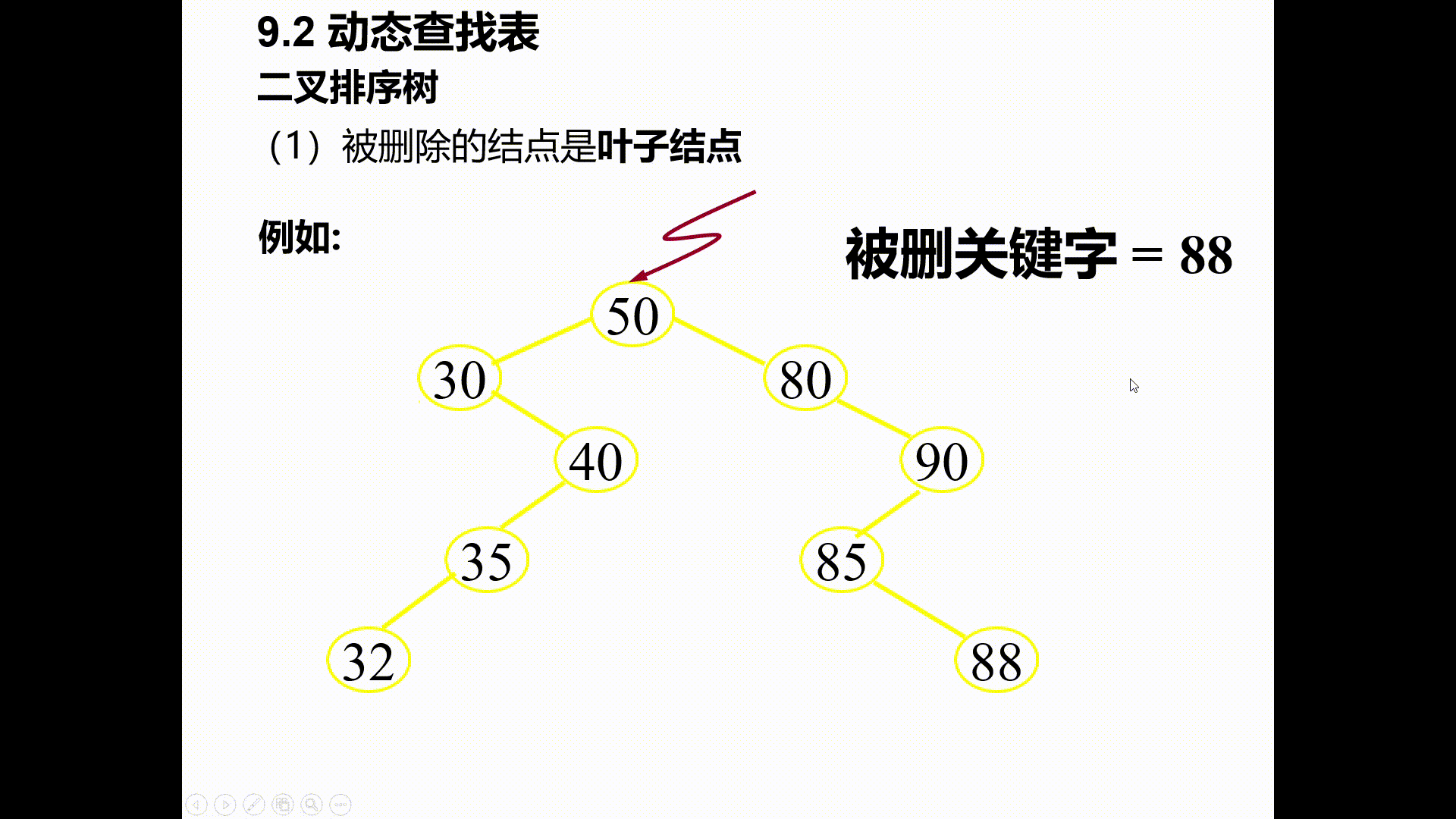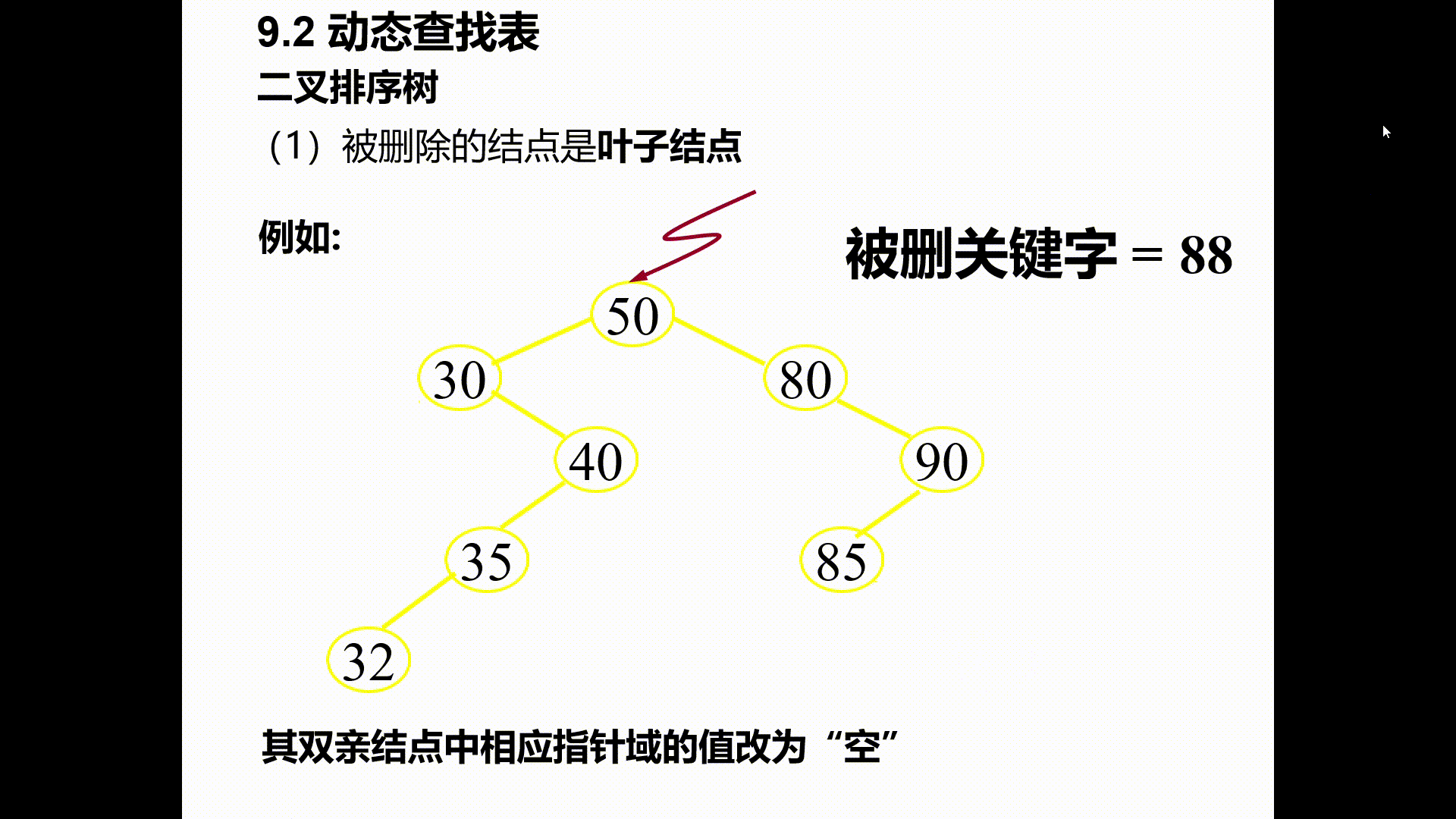
其双亲结点中相应指针域的值改为“空”

(2)被删除的结点只有左子树或者只有右子树

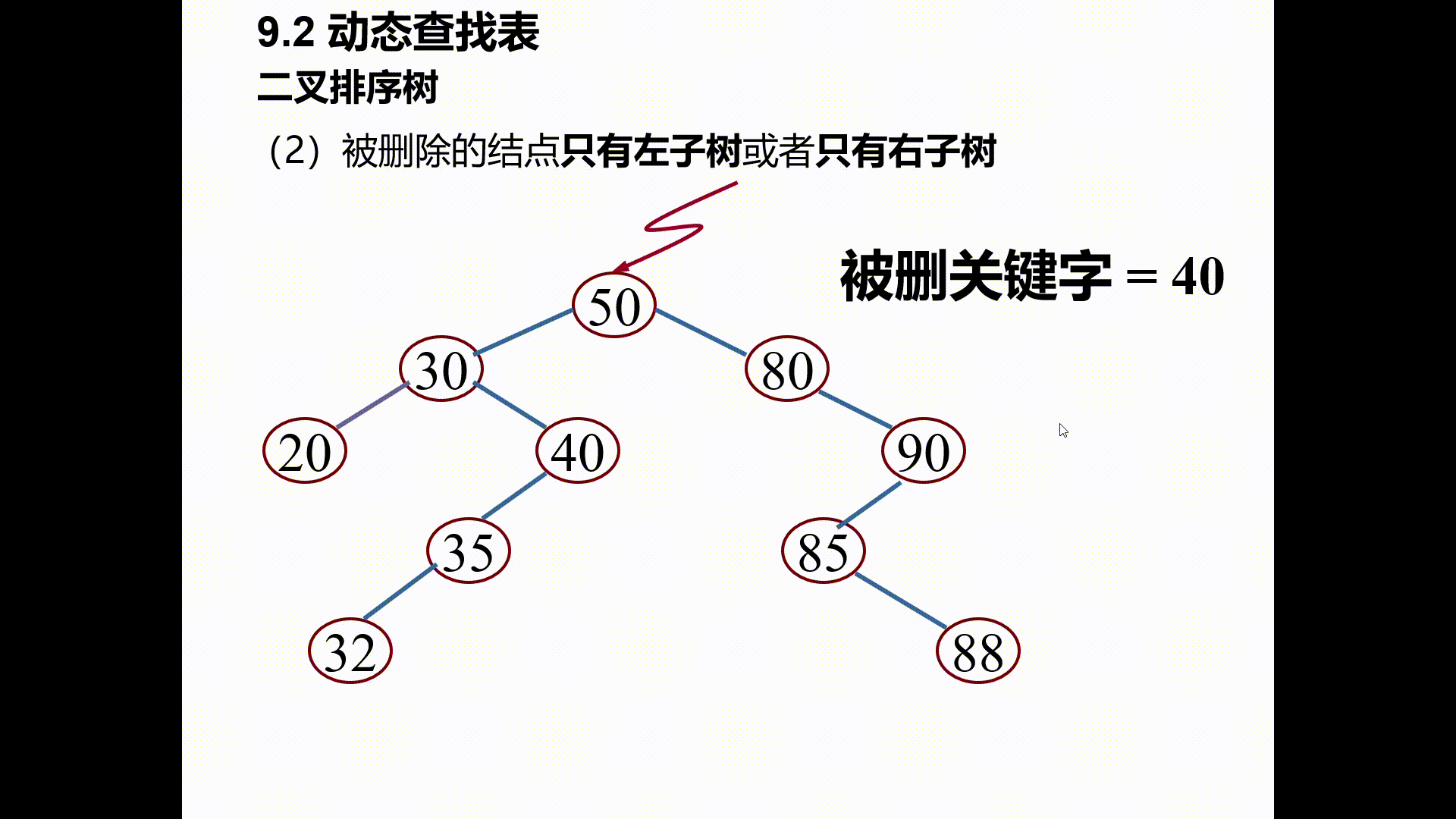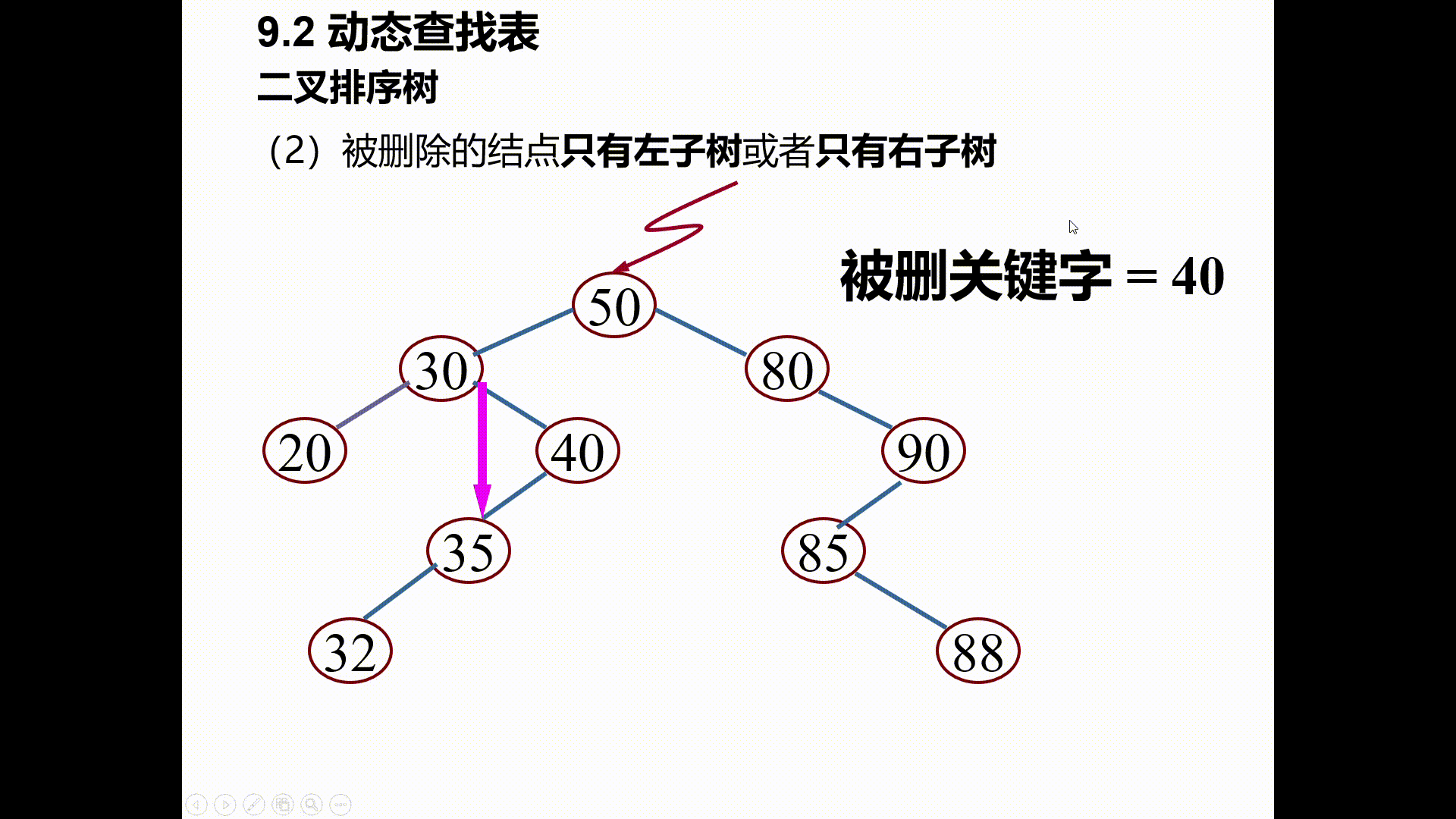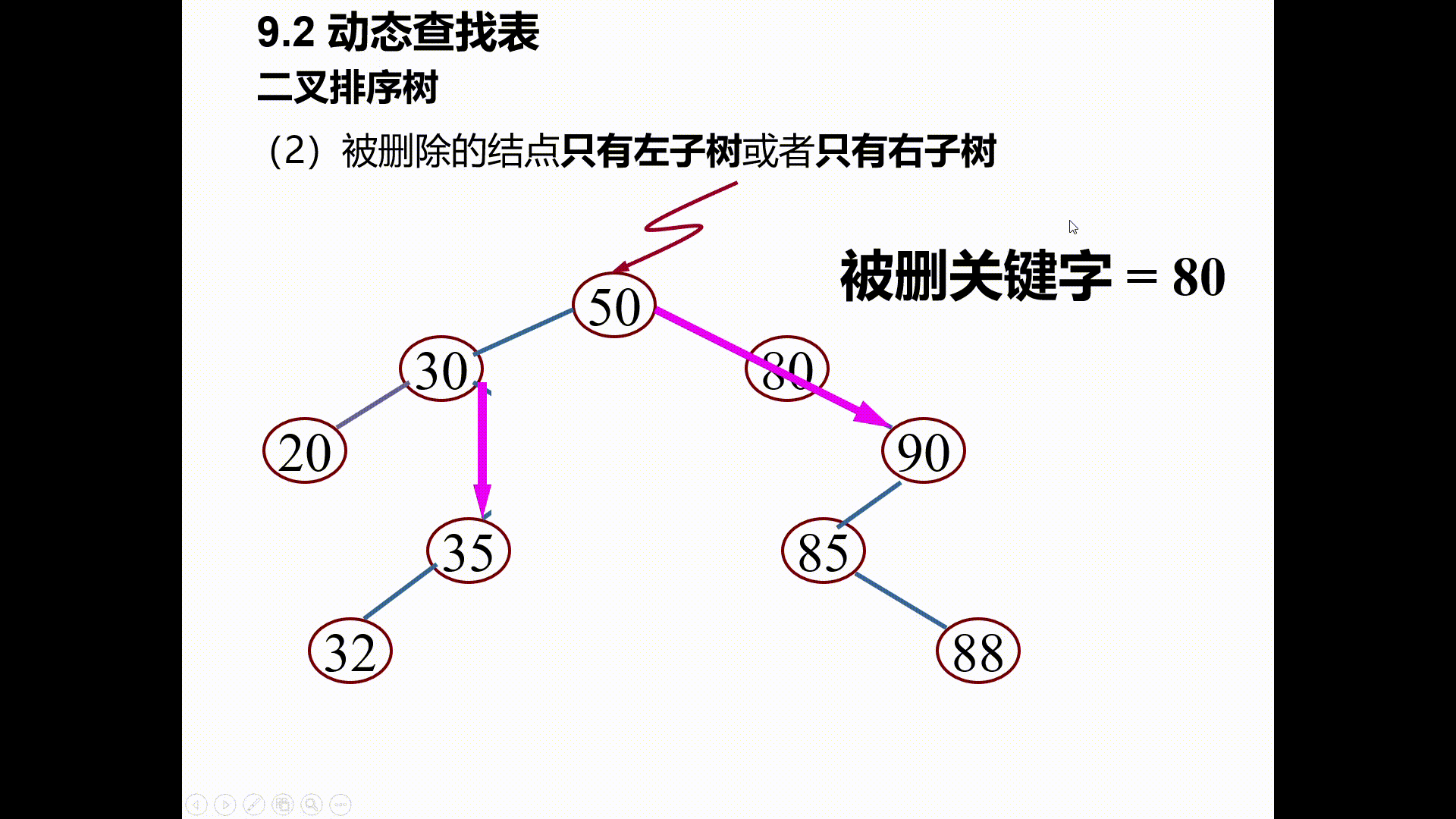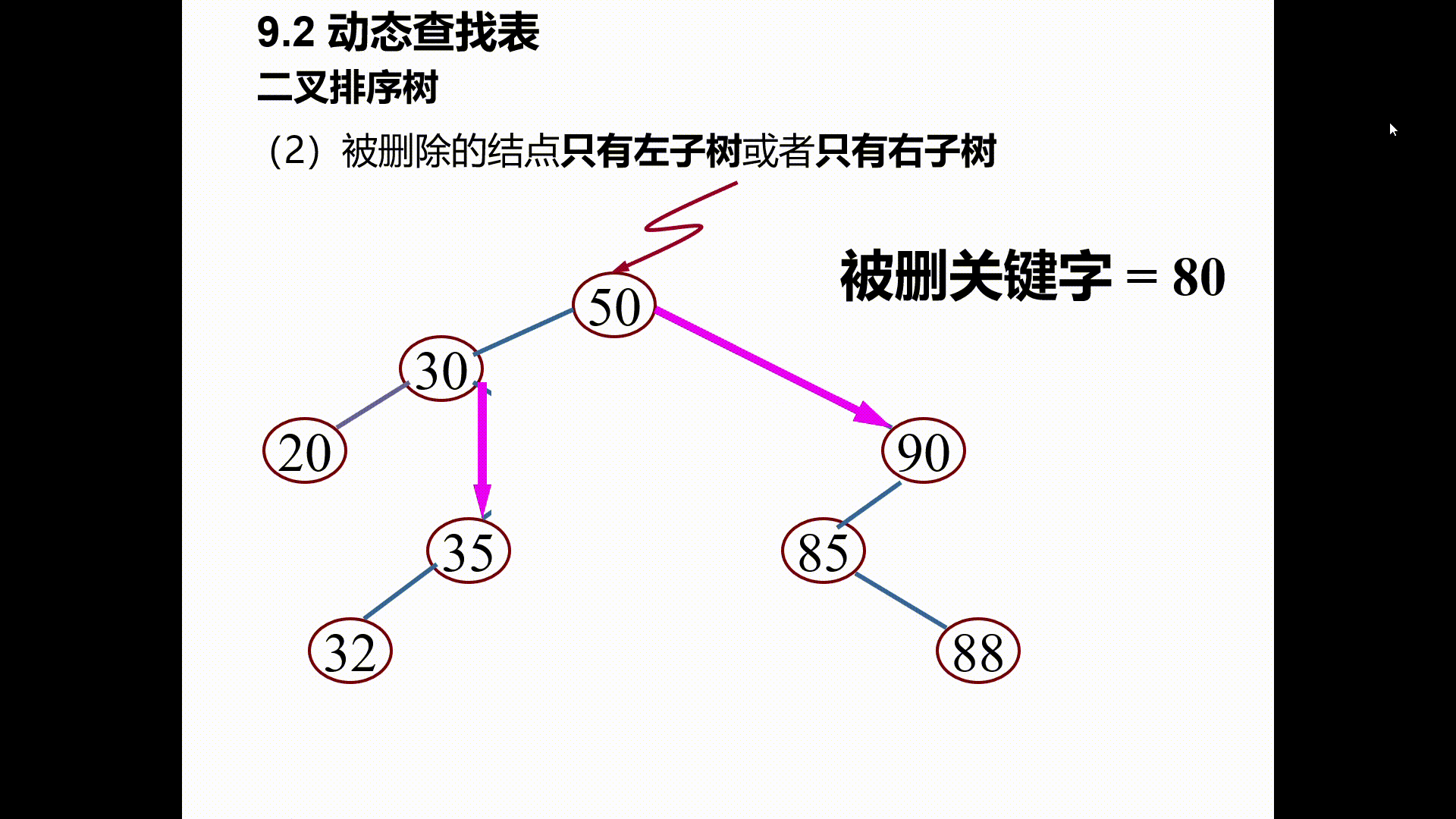
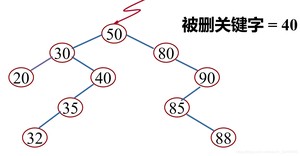
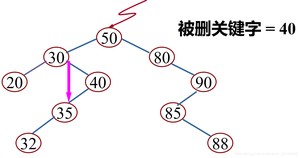
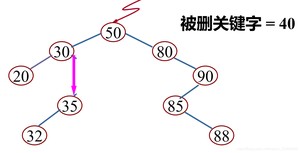
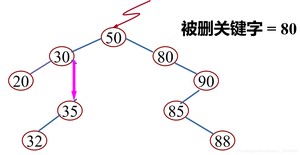
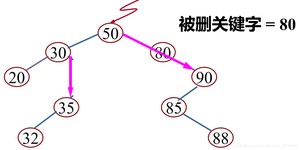
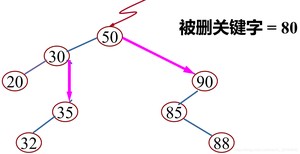
其双亲结点的相应指针域的值改为“指向被删除结点的左子树或右子树”

(3)被删除的结点既有左子树，也有右子树

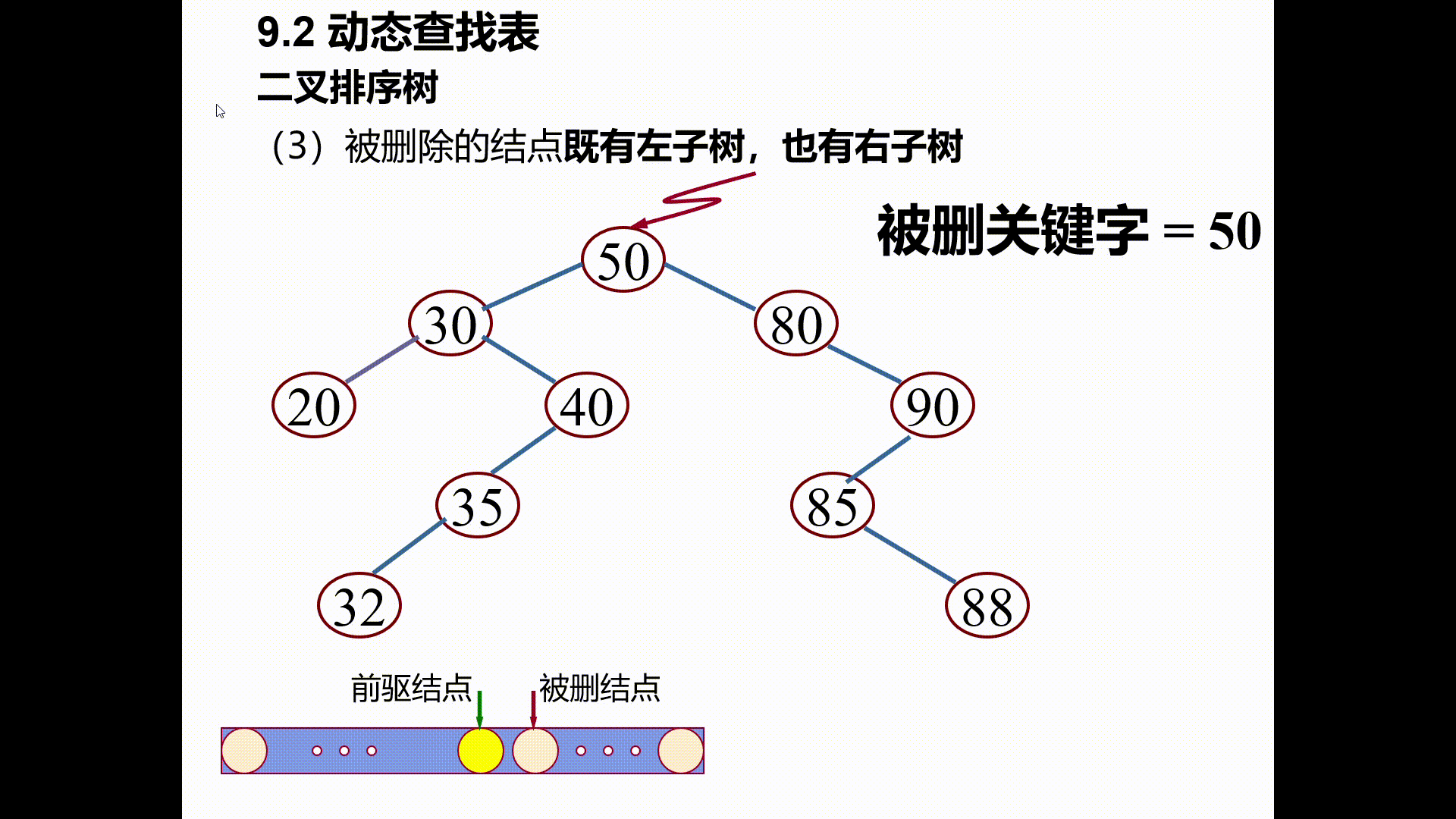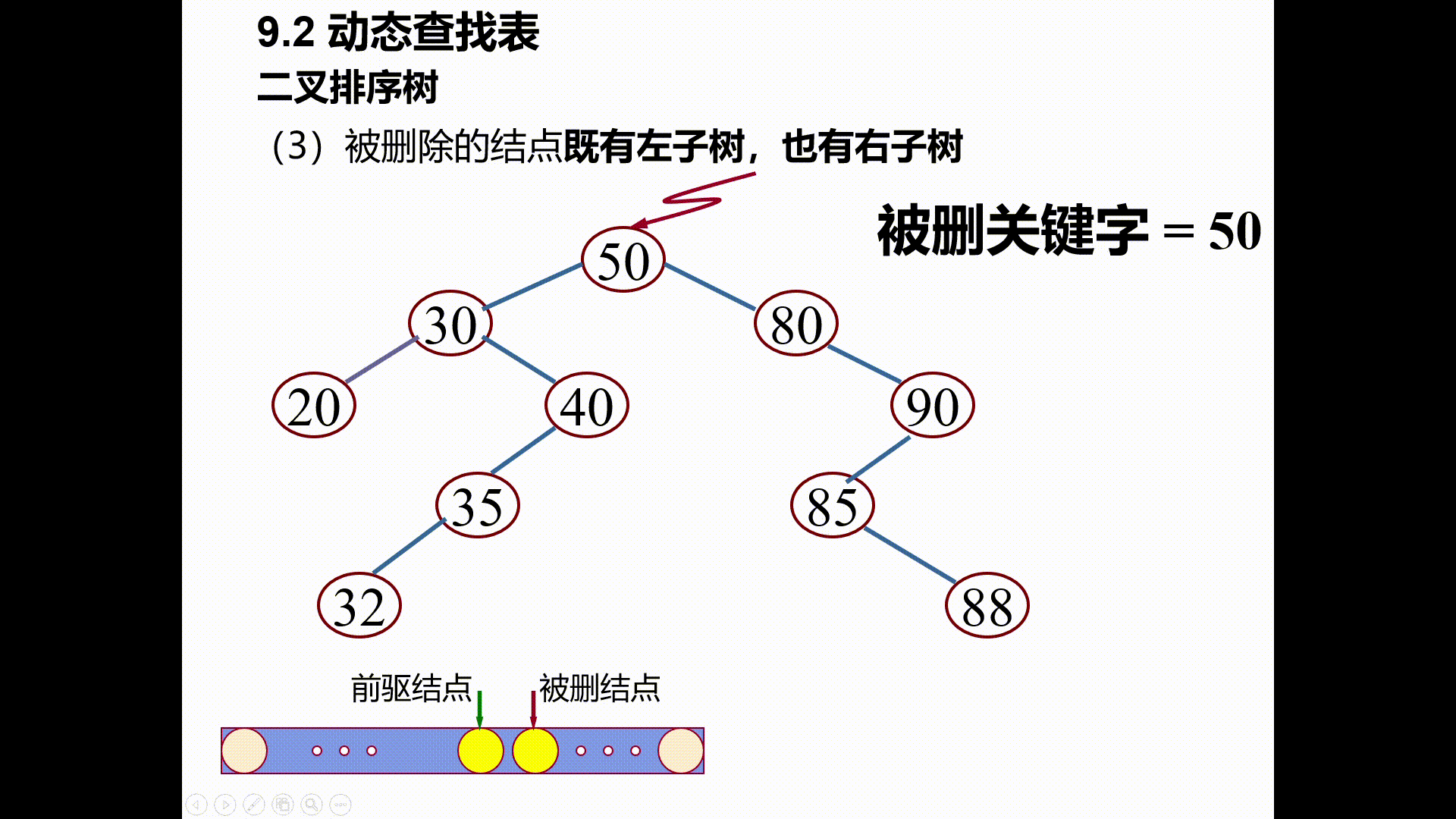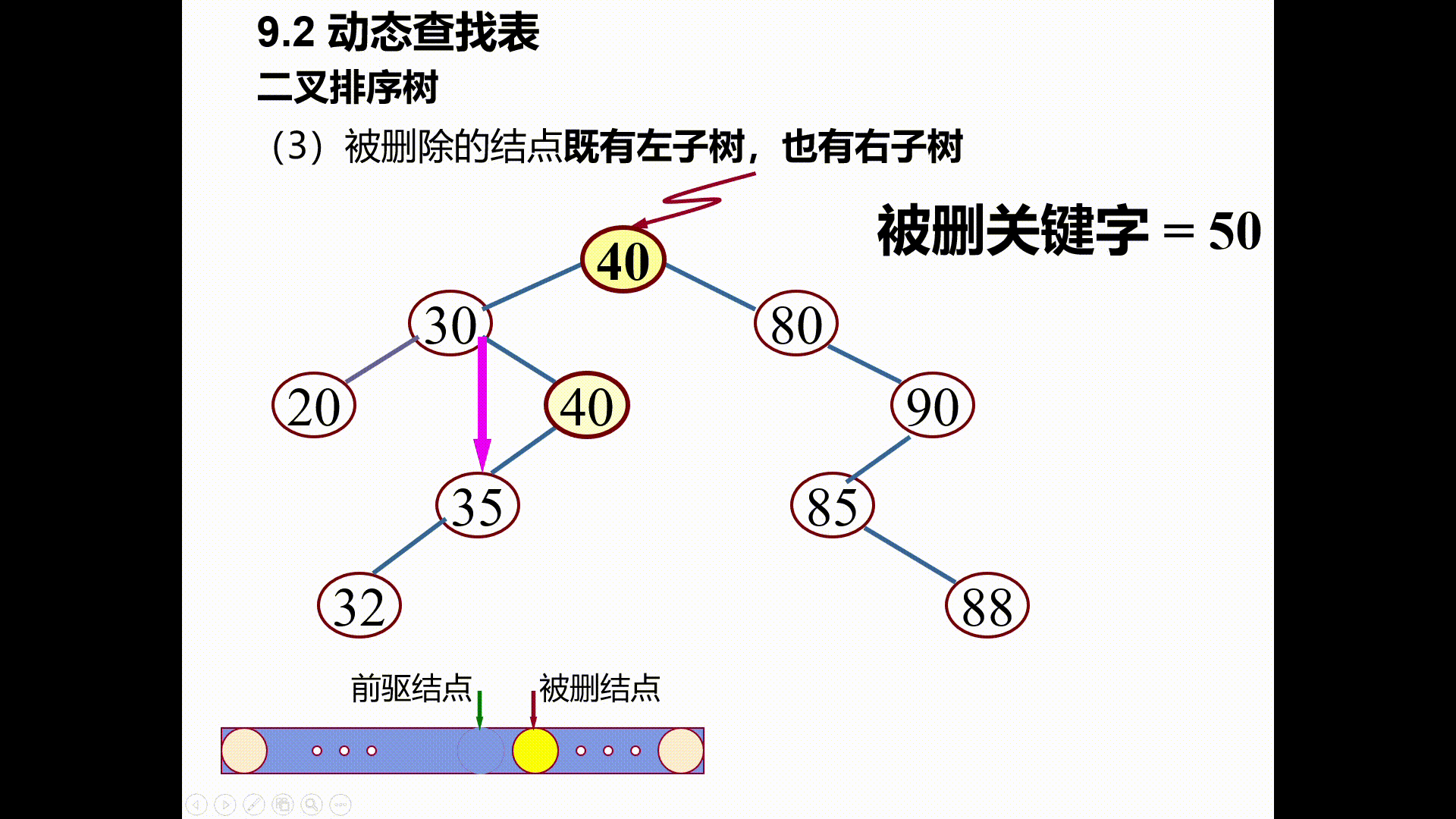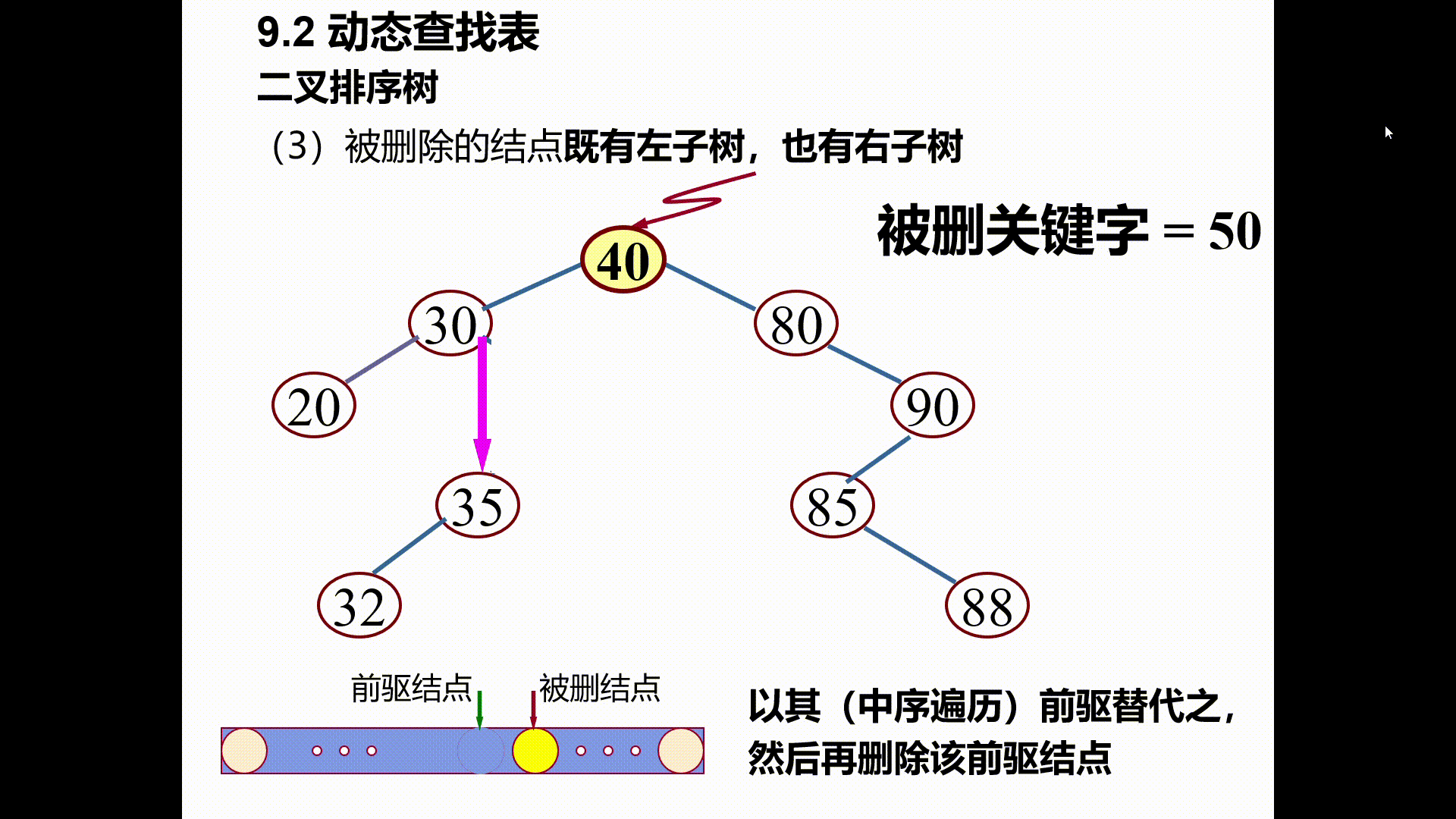
以其（中序遍历）前驱替代之，然后再删除该前驱结点

对于每一棵特定的二叉排序树，均可按照平均查找长度的定义来求它的 ASL 值，显然，由值相同的 n 个关键字，构造所得的不同形态的各棵二叉排序树的平均查找长度的值不同，甚至可能差别很大。

例如

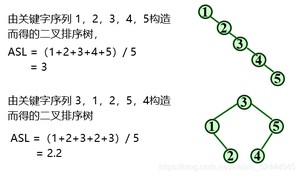
版权声明：

本文来源网络，所有图片文章版权属于原作者，如有侵权，联系删除。

本文网址：https://www.mushiming.com/mjsbk/13906.html