ElGamal 应用 1.加密;2.数字签名 密钥生成- 随机选择一个满足安全要求的1024位的大素数p,并生成有限域Zp的一个生成元g∈Zp*;
- 选择一个随机数x(1<x<p-1),计算y≡gx(mod p),则公钥为(y,g,p),私钥为Sk=x。
(随机数的选取可以使同一明文在不同时间加密成不同密文)
加解密算法- 加密过程:将明文分组比特串分组,是分组长度小于log2p,,然后对每个明文分组分别加密
- 得到公钥Pk(y,g,p);
- 消息m分组m1m2m3m4······
- 对第i块消息随机选择整数ri(1<ri<p-1);
- 计算ci≡gri(mod p),ci'≡miyri(mod p)(1≤i≤t)
- 将密文C=(c1,c1')()()()····发送给接收方 (可知,密文是明文长度的2倍)
- 解密过程
- 接收方接收密文C
- 使用密钥x和解密算法mi≡(ci'/cix)(mod p)(1≤i≤t)进行计算
- 得到明文
- 正确性
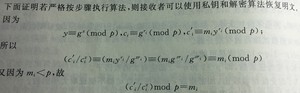
- 穷举法和列表法(二分查找算法) O(p)
- 小步大步算法
来源于生日攻击的思想,
小步为 序列1:g1,···,gj,···,gm(1≤j≤m)
大步为 序列2:y,y*g-m,···,y*g-im
找到gj≡y*g-im(mod p),即找到y=gj+im(mod p),即x=j+im私钥被找到
时间复杂度:O(p1/2)
3.指数积分法
- 选取因子基S
- 建构同余方程组:对若干随机整数k(0≤k≤p),计算gk,尝试将gk写成S中的元素幂次的乘积,即gk=∏piei(mod p),式子两边取离散对数k≡∑eilogg(pi)(mod (p-1)),重复这个过程,直到有超过m个方程
- 求logg(pi)
- 计算x:随机取整数r,计算ygrmod p,使得其值可表示为S中元素幂次的乘积,即ygr=∏pidi(mod p),取离散对数可得x≡logg(y)≡-r+∑dilogg(pi)(mod (p-1)),如果成功,即求得此解x。
背包问题:∑aixi=b,这是一个NP完全类问题
特例:超递增序列(每一个元素都比先前的元素和大) 可将背包问题转化为P类问题
公私钥对的生成- 选取素数p 和u,且bi为超递增序列
- 利用uv=1(mod p)可求得v
- a=ubk(mod p)
- {ai}和p作为公钥,{bi}和v作为私钥
- 明文消息分组
- 密文c=a1m1+···+anmn
- 利用{bi}求v c的解,可得消息m
- NP类问题,至今没有好的求解方法,能经受住穷举攻击
- 隐蔽性不够,此公钥密码是不安全的
数论中的欧拉定理,安全性依赖于大整数的素因子分解的困难性
欧拉定理:若a和n互素,则aΦ(n)≡1(mod n)
密钥生成算法
加密和解密
(1)生成公私密钥
- 选取两个大素数p和q,至少要1024位
- 计算n=p*q
- 随机选取整数e在(1≤e≤Φ(n))作为公钥,要求满足gcd(e,Φ(n))=1
- 用Euclid扩展算法计算私钥d,满足d*e≡1(mod Φ(n)),则e和n是公钥,d是私钥
(3)明文加密
c=E(m)=me(mod n)
(4)密文解密。
m=D(c)=cd(mod n)
1.算法正确性的证明

2.攻击
- 针对n分解的攻击
- 试除法
- 因子分解分析法:二次筛因子分析法
- 侧信道攻击
2.针对算法参数的攻击
1.对素数p和q选取时的限制;p和q长度相差不大,大小相差要大,否则难以抵御除法的攻击;p-1和q-1都应有大的素因子。
2.共模攻击(因此不同用户不用使用相同的p和q)
3.低指数攻击
椭圆曲线公钥加密体制 椭圆曲线韦尔斯特拉方程 :E:y²+axy+by=x³+cx²+dx+e。密码学中,常采用的椭圆曲线为: E:y²=x³+ax+b,并要求4a³+27b²≠0
Hasse定理:如果E是有限域GF(p)上的椭圆曲线,N是E上的点(x,y)(其中x,yξGF(p))的个数,则:|N-(p+1)|≤2(p)½
椭圆曲线上的点集合Ep(a,b)对于如下定义的加法规则构成一个Abel群:
- O+O=O;(O是单位元)
- 椭圆上的点P,P+O=P;
- P的逆元是-P;
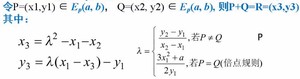
- 满足交换律
- 满足结合律
点乘规则:
- 如果k为整数,kP=P+···+P (k个P相加)
- 如果s和t为整数,(s+t)P=sP+tP,s(tP)=t(sP)
椭圆曲线点的计算:

ECC密钥生成算法
- 选择一个椭圆曲线E,构造一个椭圆群Ep(a,b)。
- 在椭圆群中挑选生成元点G=(x0,y0),需满足nG=O的最小的n是一个非常大的素数。
- 选择一个小于n的整数nB作为私钥,然后利用PB=nBG算出PB。
公钥为(E,n,G,PB),私钥为nB。
加密过程- A将明文消息编码成一个数m<p,并在椭圆群Ep(a,b)中任选一点Pt=(xt,yt);
- 在区间[1,n-1]内,A选取一个随机数k,计算P1:P1=(x1,y1)=kG;
- 依据接收方B的公钥PB,A计算点P2:P2=(x2,y2)=kPB;
- A计算密文C=mxt+yt;
- A传送加密数据Cm={kG,Pt+kPB,C}给接收方B。
- 接收方B收到Cm;
- B使用私钥nB做运算:Pt+kPB-nB(kG)=Pt+k(nBG)-nB(kG)=Pt;
- B计算m=(C-yt)/xt,得明文m。
160位的ECC密钥和1024位的RSA和1024位的ElGamal的安全性等同。
可用于加密、数字签名。 未申请专利 Rabin公钥加密体制 前言(学习意义) 具有很好的参考价值 特点不是以一一对应的陷门单向函数为基础,同一密文可能有多种明文;
破译该体制等价于对大整数的因子分解。 密钥生成算法随机选取两个大素数p和q,并且p≡q≡3mod4,将p和q作为私钥,n=pq作为公钥
加密算法 设明文块为m(m<n),运用公式c=m²modn 进行加密,c为密文。 解密算法
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/13144.html
