图像处理中滤波和卷积是常用到的操作。很多人认为卷积就是滤波,两者并无区别,其实不然。两者在原理上相似,但是在实现的细节上存在一些区别。这篇博文主要叙述这两者之间的区别。
简单来说,滤波操作就是图像对应像素与掩膜(mask)的乘积之和。
比如有一张图片和一个掩膜,如下图:
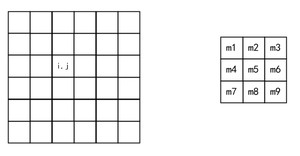
那么像素(i,j)的滤波后结果可以根据以下公式计算:
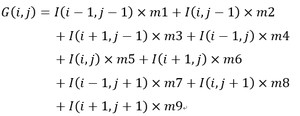
其中G(i,j)是图片中(i,j)位置像素经过滤波后的像素值。
当掩膜中心m5位置移动到图像(i,j)像素位置时,图像(i,j)位置像素称为锚点。
滤波步骤:
- 对原始图像的边缘进行某种方式的填充(一般为0填充)。
- 将掩膜划过整幅图像,计算图像中每个像素点的滤波结果。
依照这个步骤,假设我们有一个二维矩阵I,掩膜M,则滤波的结果如下:
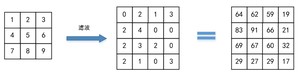
滤波后的图像大小不变。
卷积的原理与滤波类似。但是卷积却有着细小的差别。
卷积操作也是卷积核与图像对应位置的乘积和。但是卷积操作在做乘积之前,需要先将卷积核翻转180度,之后再做乘积。
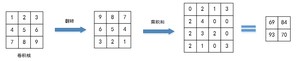
卷积步骤:
- 180度翻转卷积核。
- 不做边界填充,直接对图像进行相应位置乘积和。
从以上步骤可以看出,如果卷积核不是中心对称的,那么卷积和滤波操作将会得到完全不一样的结果。另外,卷积操作会改变图像大小!
由于卷积操作会导致图像变小(损失图像边缘),所以为了保证卷积后图像大小与原图一致,经常的一种做法是人为的在卷积操作之前对图像边缘进行填充。
最后,关于卷积后图像尺寸的计算:假设原始图像为M*M,卷积核大小为N*N,边缘填充像素个数为pad,步长为stride。则卷积后图像的尺寸变为:m =(M-N+2*pad)/sride+1。
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/12453.html
