目录
1.什么是质数?
2.如何判断是否为质数?
方法1
方法2
方法3
方法4
首先来看质数的概念:
质数(Prime number),又称素数,指在大于1的自然数中,除了1和该数自身外,无法被其他自然数整除的数。(也可定义为只有1与该数本身两个正因数的数)
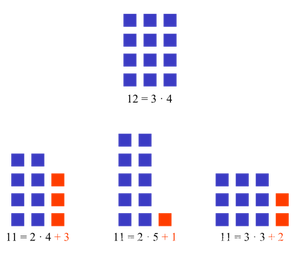
如上图所示,数字12可以将每4个分成一组,一共3组;而数字11将每4个、每5个、每3个分成一组都无法全部分完,而有剩余,因此将数字11称为质数。
质数的特点如下:
一个自然数(如1、2、3、4、5、6等)若恰有两个正约数(1及此数本身),则称之为质数。
根据质数的约数只有1和本身这一特点,可以首先想到最直观的方法。第一种方法就是判断一个数是否能被比它小的数整除。
方法1的时间复杂度是O(n)。
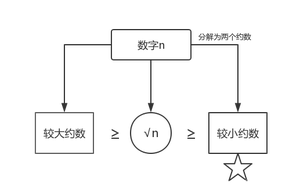
当一个数不是质数时,必定存在两个约数,一个大于等于sqrt(n),另一个小于sqrt(n)。利用这种特性,可以对方法1进行改进,只判断数n能否被小于sqrt(n)的数整除。
方法2的时间复杂度是O(sqrt(n))。
任一偶数一定能分解为2和其他偶数/奇数的积,因此一个数不能被2整除,那么这个数一定不能被其他偶数整除。利用这个特点,可以对方法2进行改进,判断数n能否被小于sqrt(n)的奇数整除。
方法3的时间复杂度是O(sqrt(n)/2)。
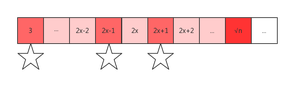
质数的分布具有特点,经过证明可以得到,(大于等于5的)质数一定和6的倍数相邻,一定是6x-1或6x-1。利用这种特性。可以对整数进行筛选,只判断那些是6x-1或6x-1的整数是否为质数。
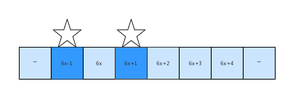
证明过程如下:
令x≥1,将大于等于5的自然数表示如下: ······6x-1,6x,6x+1,6x+2,6x+3,6x+4······(相邻6个数为一组)
在以上的数字中,6x、6x+2和6x+4是偶数,一定不是质数;6x+3可以分解为3(2x+1),不是质数,因此质数只能是6x-1和6x+1。
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/12049.html
