目录
一、01背包问题
二维dp解法：
一维dp解法：
二、完全背包问题
编辑
朴素写法（三重循环）：
第一次优化：
第二次优化：
三、多重背包问题
多重背包I
思路：
多重背包II
二进制优化方法：
四、分组背包问题
思路：
有 N 件物品和一个容量是 V的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi，价值是 wi。
输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。
接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数，表示最大价值。
数据范围
输入样例
输出样例：
二维dp解法：
动态规划数组定义：
表示只考虑前件物品，当背包容量为时的最大价值。
初始化：
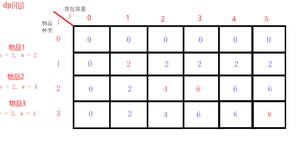
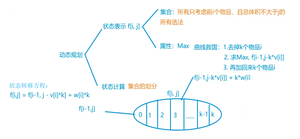
由上图，我们可以清楚的知道01背包最大价值是如何推出的
状态转移方程：对于每个物品，我们有两种选择：不放入背包，或者放入背包。如果不放入背包，那么；如果放入背包，前提是背包的容量大于等于物品的体积，那么。选择这两种情况的最大值作为的值。
循环遍历：
当前背包容量为 i 时所得最大价值，必不小于背包容量为 i - 1 时的最大价值，故先令此时背包容量的最大价值为 f[i - 1][j]，再判断是否能放的下每个不同的物品，如果能放下，则比较后取较大的值。
一维dp解法：
动态规划数组定义：
表示背包容量为时，能装入的最大价值。
状态转移方程：
对于每个物品，考虑是否放入背包中。若不放入，则总价值不变；
若放入，则总价值为（在当前容量下，放入物品后的总价值）。
因此，状态转移方程为。
循环遍历：
在01背包问题中，每个物品只能放一次进背包。
如果我们从最小的背包容量开始考虑放物品（即正序遍历），那么在更新较大的背包容量 时，较小的背包容量 可能已经考虑过了物品 。这会导致物品 被错误地计算两次，即它在更新 时被考虑过一次，在更新 时又被考虑。因为逆序是从大到小考虑，所以，并不会发生上述重复考虑的情况（ ）
我们发现i与i - 1 差了1, 所以顺序无法得出答案，所以我们选择逆序。
外层循环遍历所有物品。
内层循环从逆序遍历到（物品体积），确保每个物品只被计算一次，防止一个物品被重复计算（即确保每个物品只被放入一次）。
有 N 种物品和一个容量是 V 的背包，每种物品都有无限件可用。
第 i 种物品的体积是 vi，价值是 wi。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。输出最大价值。
接下来有 N 行，每行两个整数 vi, wi，用空格隔开，分别表示第 i 种物品的体积和价值。
数据范围：
0 < N, V ≤ 1000
0 < vi, wi ≤ 1000
输入样例
输出样例：
朴素写法（三重循环）：
解题思路：
动态规划数组定义：
使用二维数组，其中表示考虑前件物品，当背包容量为时的最大价值。
状态转移方程：
，这个方程考虑了不选取当前物品和选取当前物品次两种情况下的最大价值，并取这些情况的最大值更新DP数组。
循环遍历：
- 外层循环遍历所有物品，中层循环遍历所有可能的背包容量。
- 内层循环遍历每个物品的可能选取次数（即物品可以被选取0次、1次、2次，直到超过当前背包容量）。
- 对于每种情况，更新为，表示考虑选取次物品时的最大价值。
第一次优化：
解题思路：
动态规划数组定义：
使用二维数组，其中表示考虑前件物品，当背包容量为时的最大价值。
状态转移方程：
循环遍历：
和01背包二维dp类似，当前背包容量为 i 时所得最大价值，必不小于背包容量为 i - 1 时的最大价值，故先令此时背包容量的最大价值为 f[i - 1][j]，再判断是否能放的下每个不同的物品，如果能放下，则比较后取较大的值。
第二次优化：
与01背包一维dp类似，但是此处是顺序。
对于完全背包，由于每种物品可以取无限次，我们希望每个物品能够被重复考虑。因此，我们采用正序遍历背包容量的方式（即从 v[i] 到 m）。这样，在更新 f[j] 的时候，f[j-v[i]] 总是表示未选择当前物品 i 时的最大价值，因此当前物品可以被多次加入背包中，只要不超过背包容量。
因为顺序从小到大考虑，已经让每个物品被重复多次的考虑了（已经多次重复考虑计算之前的物品，顺序时，只要有能放入的空间，就放入物品）
有 N 种物品和一个容量是 V 的背包。
第 i 种物品最多有 si 件，每件体积是 vi，价值是 wi。
求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。输出最大价值。
接下来有 N 行，每行三个整数 vi, wi, si，用空格隔开，分别表示第 i 种物品的体积、价值和数量。
数据范围：
0 < N, V ≤ 100
0 < vi, wi, si ≤ 100
输入样例
思路：
完全背包问题是第i件物品可以选任意多个，而多重背包只限制了第i件物品最多选s[i]个。
加上这条限制即可
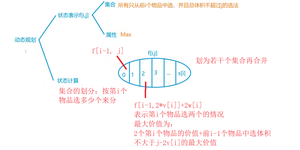
状态转移方程：
循环遍历：
外层循环：循环遍历所有物品
中层循环：循环遍历所有可能的背包容量
此时的时间复杂度为：100*100*100，可以正常运行。
此题如果直接使用，时间复杂度为：
有 N 种物品和一个容量是 V 的背包。
第 i 种物品最多有 si 件，每件体积是 vi，价值是 wi。
求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。输出最大价值。
接下来有 N 行，每行三个整数 vi, wi, si，用空格隔开，分别表示第 i 种物品的体积、价值和数量。
数据范围：
0 < N ≤ 1000
0 < V ≤ 2000
0 < vi, wi, si ≤ 2000
提示：
本题考查多重背包的二进制优化方法。
输入样例
输出样例：
思路：
该题与多重背包I的区别是数据范围变大，此时如果仍使用多重背包I中的方法，此时的时间复杂度为：1000*2000*2000 = 40亿，，时间复杂度过大需要优化。
二进制优化方法：
简而言之，就是先把同类的物品拆分成不同的组，拆分完一类物品后，再去拆下一个，将所有物品都拆分好后，就将多重背包问题转化为了01背包问题。
给定N组物品和一个容量为V的背包。每组物品包含若干个，但在同一组内，你最多只能选择一件物品。每件物品有其对应的体积和价值。目标是选择一些物品放入背包，使得背包内物品的总体积不超过背包的容量，同时背包内物品的总价值尽可能大。
输入：
第一行输入包含两个整数N和V，分别代表物品组数和背包的容量。
接下来是N组数据。每组数据的第一行包含一个整数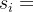
，代表第i组的物品数量。
每组数据接下来的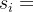行，每行包含两个整数
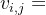和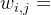
，分别代表第i组中第j个物品的体积和价值。
输出：
输出一个整数，代表可以放入背包中的物品的最大价值。
数据范围：
0 < N, V ≤ 100
0 < Si ≤ 100
0 < vij, wij ≤ 100
输入样例
输出样例：
思路：
分组背包问题就是在01背包问题的基础之上，多了一个在每个组中选出最优的那个物品（或者不选）。
对于每一组物品，尝试将组中的每个物品放入背包中，看看是否能够得到更大的价值。注意，中层循环是从背包容量m到0的逆序遍历，这是为了防止同一个组中的物品被重复放入背包（即保证每组中至多选择一个物品）。
今天就先到这了！！！
版权声明：
本文来源网络，所有图片文章版权属于原作者，如有侵权，联系删除。
本文网址：https://www.mushiming.com/mjsbk/11091.html