设是一个连通图,的一个生成子图若本身是一棵树,称它为的一棵生成树。任何连通图都有生成树。
不难看出,有个顶点的连通图的生成树必定有条边,生成树是连通图的极小子图,在生成树中任意增加一条边,必定产生回路。
✅设是一个带权连通图,其生成树上任一条边的权值称为该边的代价的一棵生成树T的代价就是生成树中各边的代价之和。在的所有生成树中,代价最小的生成树称为最小代价生成树,简称最小生成树。
✅最小生成树的生成准则:
- 只能选用该图中的边来构造最小生成树。
- 必须使用且仅能使用条边来连接连通图中的个顶点。
- 选用的n-1条边不能产生回路。
- 尽量选取权值小的边。
- Kruskal算法:通常适用于稀疏图
- Prim算法:通常适用于稠密图
🏆1.3.1Kruskal算法
算法是一种按照权值的递增次序选择合适的边来构造最小生成树的方法。
🔎设是一个具有个顶点的带权连通无向图,是的最小生成树,则构造最小生成树的步骤如下:
- 构造一个由个顶点组成,不含任何边的图,即为空集(其中每个顶点构成一个连通分量)。
- 不断从中取出代价最小的一条边,若该边未使形成回路(即该边的两个顶点来自中不同的连通分量),则将此边加入到中,否则舍去此边选择下一条代价最小的边。以此类推,知道中包含条边。
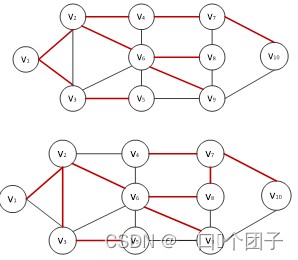
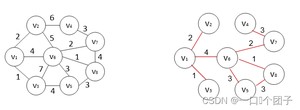
🎠Kruskal算法示例:
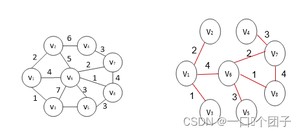
🏆1.3.2Prim算法
🔎设是一个具有个顶点的带权连通无向图,是的最小生成树,则构成最小生成树的步骤如下:
- 设置一个集合,在图上任选一个点加入,算法从,开始,重复执行下列操作。
- 在所有属于属于的边中找一条代价最小的边并入集合同时并入直至为止。此时中必有条边,为的最小生成树。
🎠Prim算法示例:
有向无环图是一个无环的有向图,简称图。的两个典型应用。
在现代管理系统中,人们常用有向图来描述和分析一项工程的计划和实施过程,一个工程常被分为多个子工程,这些子工程被称为活动。在有向图中若以顶点表示活动,有向边表示活动之间的优先关系的图称为。
若是图中的有向边,则是的直接前驱;是的直接后继。若存在一条从到的路径,则称是的前驱,是的后继。网中不允许有回路,若存在回路,则意味着某项活动以自己为先决条件。
🏆2.1.1拓扑排序方法
🔎拓扑排序的方法:
- 从有向图中选一个没有前驱的顶点并输出之。
- 从图中删除该顶点和所有以它为尾的弧。
- 重复上述两个步骤,直至全部顶点均已输出;或者当图中不存在无前驱的顶点为止(此时说明图中有环)。
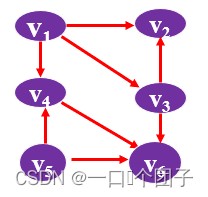
📝对于上图,拓扑排序的序列为:V1 V5 V4 V3 V2 V6
注:拓扑排序的结果不一定唯一!
🏆2.1.2拓扑排序的算法流程
✅拓扑排序算法流程如下:
(1).把邻接表中入度为的顶点依次进栈。
(2).若栈不空,则栈顶元素退栈并输出,在邻接表中查找的直接后继,把的入度减;若的入度为,则进栈,继续该过程。
(3).若顶点个数不为(为有向图的顶点数),则有向图有环;否则,拓扑排序完毕。
带权的有向无环图,称为网,其中顶点表示事件,弧(有向边)表示活动,权表示活动持续时间。在工程上常用工程进度计划。通常每个工程只有一个开始事件和一个结束事件,在表示工程的网中,表示整个工程的开始点(入度为的顶点)称为。表示整个工程的结束点(出度为的顶点)称为汇点。在上,从源点到汇点的路径长度最长的一条路径,或者全部由关键活动(即不按期完成就会影响整个工程完成的活动)构成的路径称为关键路径。
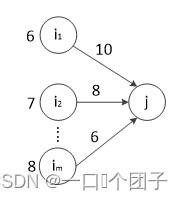
🏆2.2.1事件的最早发生时间(ve)
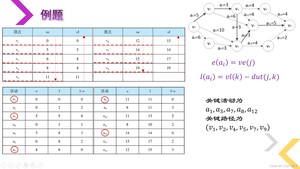
设网有个顶点,用表示源点,表示汇点,表示网中的第个顶点。事件j的最早发生时间从源点到结点的最长的路径,意味着事件最早能够发生的时间,这个时间决定了所有以j为头的弧所表示的活动的最早开始时间。源点的最早发生时间为,即,从开始向汇点递推,设事件是事件i的直接后继,则其中是所有以顶点为尾,顶点为头的弧的集合。
若顶点旁边的值代表顶点的最早发生时间,则.
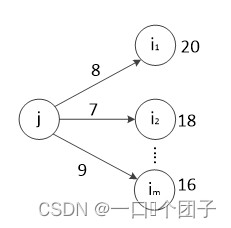
🏆2.2.2事件的最迟发生时间(vl)
事件的最迟发生时间:不影响工程的如期完成,事件j必须发生的时间。汇点的最迟发生时间即汇点的最早发生时间等于最迟发生时间,从开始向源点递推。设事件j是事件i的直接前驱,则其中,是所有以为顶点,顶点为尾的弧的集合。
图中若顶点旁边的值代表该顶点的最迟发生时间,则.
🏆2.2.3例题

版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/10969.html