写这篇文章,真的花了我很多功夫,希望能够对看到的大家有所帮助啦
首先,KMP算法的作用是进行模式串的匹配
也就是对于一个已知的长字符串t,我们在其中找到,与模式串m完全相同的部分,并且返回相同部分的首数组标号
采用BF算法,能够非常直观求出匹配位置,但是由于指针回溯,进行了多余的比较,非常缓慢
这样就有了KMP算法的诞生

下文中,我们将待比较的字符串,存入下面这样的结构体中:
我们发现,可以减少BF算法比较次数的原因在于,BF算法中,每一次模式串的指针回移太长了
我们发现将如下图的指针i和j全部回移,归位,就会多进行很多无用的比较
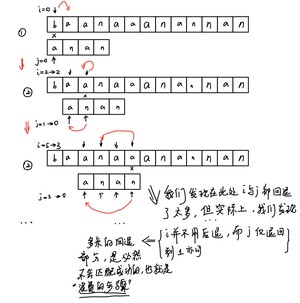
我们之所以知道多余的回退是没有用的,是由模式串本身的特性决定的
我们已知,即使在出现不匹配时,不匹配处的左侧的字符串和主串对应位置,是相同,或者说匹配的.
就像上图中一样,进行到第三步的时候(图中标错了),前面的"ana"在主串和模式串中,都是相同的
我们可以考虑引入一个概念,也就是"最大公共前后缀",假设其位数为n位
也就是从该部分匹配串的第一位开始往后数n位,和此部分匹配串的最后一位开始往前数n位,两者完全相同
当然也会有"次大公共前后缀",但是如果是次大的话,就会出现回移过少,漏掉了可能性的情况
我们必须考虑最大的公共前后缀,让j指针回移最多,并且不会漏掉可能性,从而最大程度得节约步骤和考虑全面.这样一个最佳位置,其实就是最大公共前后缀的位数.
使用KMP的过程中,我们不回移i指针,仅仅将j指针回移到左边的"部分匹配串"的"最大公共前后缀"中的前缀的后一位的位置,重新继续与主串匹配
我们的next数组,与模式串的长度相同
其中,记录的就是当前位置左边的"部分匹配串"的最大公共子串长度n
也是j指针接下来要移动到的位置,在下图中已经说明了.
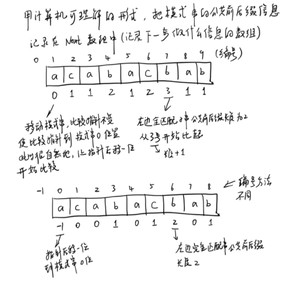
下面的代码是用上图中的第二种编号方法写出的:


为什么要引入nextval数组呢?
其实上文中认为next数组就是模式串回退的最佳位置,其实是不对的
next数组中保存的是"当前位置左边部分匹配串"的"最大公共前后缀"的位数n或者是n-1(没有本质差别)
虽然next数组能用,它确实大大优化了模式串的后移位数,并且不会遗漏正确结果,但是它仍不是,效率最高的后移位置


为什么nextval数组更加优化了?

nextval数组是怎样得到的?
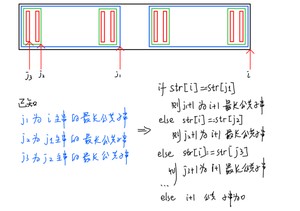
是在已知next数组的基础上,进行如下规则的判断得到的:
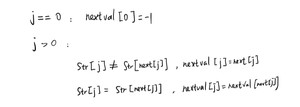
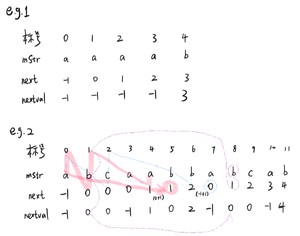
求next和nextval数组的例子如下,可以跟着线条多画几遍,就能够熟练了:
就拿下图中eg2中数据为例,在模式串为0位置处,next和nextval数组的值都必然是-1,这是默认不变的
- 首先,求next数组的方法就是:
首先以位置5为例:
要求出位置5的next值,必须要看位置5-1(=4)的next值
比较位置4的字符和next [ 4 ] (=1)位置的字符,如果相等,则5位置存入next[4]+1
若不等,则比较位置4字符和next [ next [ 4 ] ] (=0)的字符,如果相等,则存入next [ next [ 4 ] ] +1(=1)
然后,以位置7为例,考虑一种特殊情况,也就是到了最后也没有匹配成功的情况:
求7看6,'b’为标准,向前找到2号c,不匹配
再向前找到0号’a’,仍然不匹配,则直接返回(-1+1)=0
总结一下求next值方法!!!
前位字符为标准,next值作模串标号向前跳,匹配则返回该标号加1,不匹配继续向前跳,0号还不匹配直接返回0
- 在next数组的基础上,求nextval的方法就是:
以位置8为例:
求nextval数组,直接以当前位置的next值作为标号,向前跳一位,比较当前位和前跳位字符
1.匹配,则当前位nextval值,等于前跳位nextval值
2.不匹配,则当前为nextval值,直接等于当前位next值
总结一下求nextval值方法!!!
当前位字符为标准,next值为模串标号向前跳一位,匹配nextval值等于前跳位,不匹配当前位next值直接落下来
将匹配起始点结果存入P数组中
可以灵活根据需要,修改这段代码,可以参考以下例子:
https://blog.nowcoder.net/n/2dcba84e8096a41196ee5c6506
调整之后,就能够存入符合特定要求的匹配串了
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/10022.html
